A marble is allowed to roll down an inclined plane from a fixed height. At the foot of the inclined plane, it moves on a horizontal surface (a) covered with silk cloth (b) covered with a layer of sand and (c) covered with a glass sheet. On which surface will the marble move the shortest distance. Give reason for your answer.
covered with silk cloth
covered with a layer of sand
covered with a glass sheet
none of these
The correct Answer is:B
To determine on which surface the marble will move the shortest distance after rolling down an inclined plane, we need to analyze the effects of friction on each surface.
1. Understanding the Scenario:
- A marble rolls down an inclined plane and reaches the bottom where it encounters three different surfaces: silk cloth, sand, and a glass sheet.
2. Identifying the Surfaces:
- Silk Cloth: This surface is smooth and has low friction.
- Sand: This surface is rough and has high friction.
- Glass Sheet: This surface is also smooth but typically has slightly higher friction than silk.
3. Effect of Friction:
- Friction opposes the motion of the marble. The greater the friction, the shorter the distance the marble will travel.
- The rougher the surface, the more friction it produces.
4. Comparing the Surfaces:
- On the silk cloth, the marble will experience minimal friction, allowing it to roll a longer distance.
- On the glass sheet, the friction is low but higher than that of silk, so the marble will roll a shorter distance than on silk but longer than on sand.
- On the sand, the roughness creates significant friction, which will greatly oppose the marble's motion, causing it to stop much sooner.
5. Conclusion:
- Since sand has the highest friction among the three surfaces, the marble will travel the shortest distance on the sand. Therefore, the answer is that the marble will move the shortest distance on the surface covered with sand.
Final Answer:
The marble will move the shortest distance on the surface covered with sand due to the high friction that opposes its motion.
---
- A marble rolls down an inclined plane and reaches the bottom where it encounters three different surfaces: silk cloth, sand, and a glass sheet.
- Silk Cloth: This surface is smooth and has low friction.
- Sand: This surface is rough and has high friction.
- Glass Sheet: This surface is also smooth but typically has slightly higher friction than silk.
- Friction opposes the motion of the marble. The greater the friction, the shorter the distance the marble will travel.
- The rougher the surface, the more friction it produces.
- On the silk cloth, the marble will experience minimal friction, allowing it to roll a longer distance.
- On the glass sheet, the friction is low but higher than that of silk, so the marble will roll a shorter distance than on silk but longer than on sand.
- On the sand, the roughness creates significant friction, which will greatly oppose the marble's motion, causing it to stop much sooner.
- Since sand has the highest friction among the three surfaces, the marble will travel the shortest distance on the sand. Therefore, the answer is that the marble will move the shortest distance on the surface covered with sand.
The marble will move the shortest distance on the surface covered with sand due to the high friction that opposes its motion.
Topper's Solved these Questions
- FRICTIONBOOK - NCERT EXEMPLARCHAPTER - FRICTIONEXERCISE - LONG ANSWER QUESTIONS
3 Videos
- FRICTIONBOOK - NCERT EXEMPLARCHAPTER - FRICTIONEXERCISE - VERY SHORT ANSWER QUESTIONS
3 Videos
- FORCE BOOK - NCERT EXEMPLARCHAPTER - FORCE EXERCISE - SHORT ANSWER QUESTIONS
9 Videos
- LIGHTBOOK - NCERT EXEMPLARCHAPTER - LIGHTEXERCISE - LONG ANSWER QUESTIONS
9 Videos
Similar Questions
A small bar starts sliding down an inclined plane forming an angle α with the horizontal. The friction coefficient depends on the distance x covered as k=ax, where a is a constant. Find the distance covered by the bar till it stops, and its maximum velocity over this distance.
View Solutionbody with zero initial velocity moves down an inclined plane from a height hand then ascends along the same plane with an initial velocity such that it stops at the ame height h. In which case is the time of motion longer?
View Solution
Knowledge Check
A block slides down a smooth inclined plane and then moves on to a rough horizontal surface. Which of the following is/are correct? (Neglect impulsive effect at the bottom of incline)
 AThe graph of velocity as a function of time is
AThe graph of velocity as a function of time is
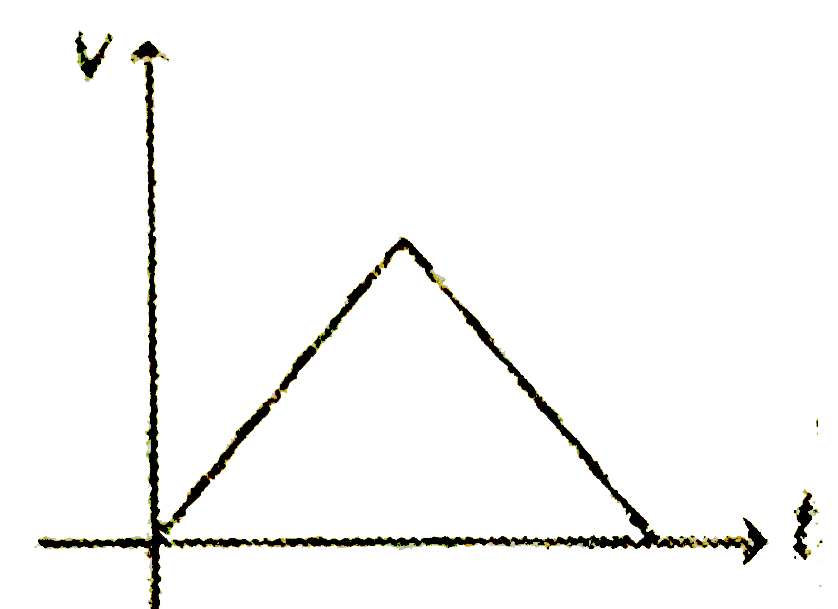 BThe graph of acceleration as a function of time is
BThe graph of acceleration as a function of time is
 CThe graph of mechanical energy as a function of time is
CThe graph of mechanical energy as a function of time is
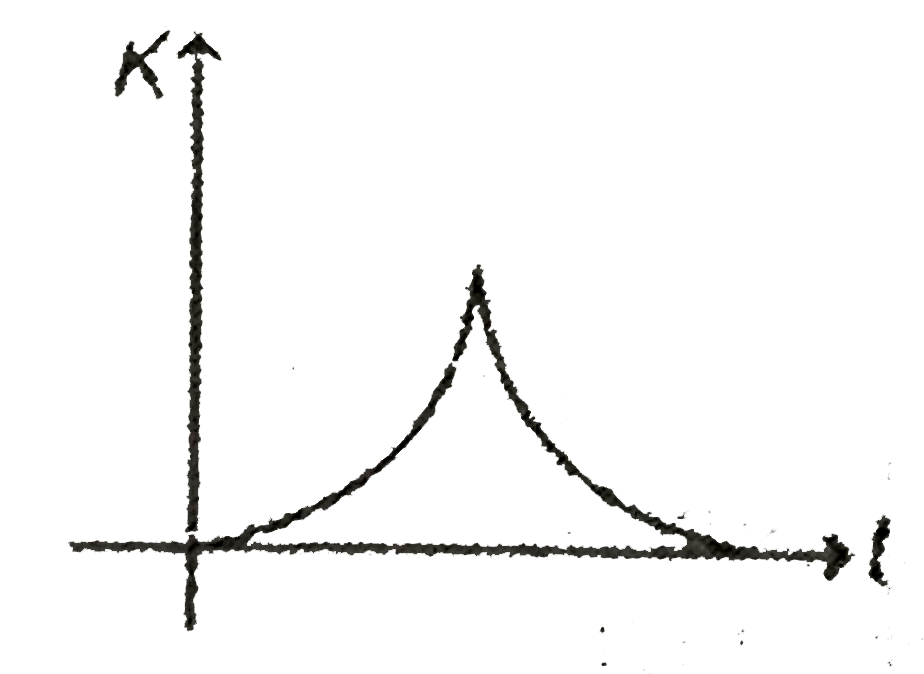
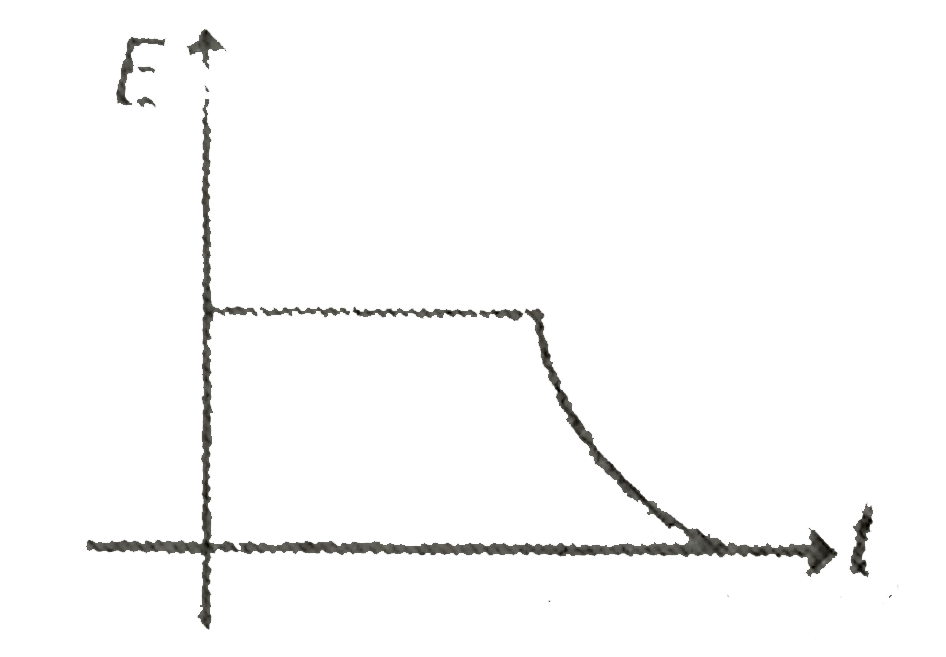 DThe graph of kinetic energy as a function of time is
DThe graph of kinetic energy as a function of time is
A particle of mass m comes down on a smooth inclined plane from point B at a height of h from rest. The magni-tude of change in momentum of the particle between position A (just before arriving on horizontal surface) and C (assuming the angle of inclination of the plane as θ with respect to the horizontal) is
 A0B2m√(2gh)sinθC2m√(2gh)sin(θ2)D2m√(2gh)
A0B2m√(2gh)sinθC2m√(2gh)sin(θ2)D2m√(2gh)A small mass slide down an inclined plane of inclination theta with the horizontal. The coefficent of friction is μ=μ0 x where x is the distance through which the mass slide down and μ0,a contant. Then the speed is maxmum after the mass covers a distance of.
Acosθμ0Bsinθμ0Ctanθμ0D2tanθμ0
A block sliding down on an inclined plane forms an angle θ with the horizontal. The friction coefficient depends on the distance x covered as μ=kx , where k is a constant. Find the distance covered by the block till it stops and its maximum velocity over this distance. Also , sketch a graph between square of velocity and distance covered x.
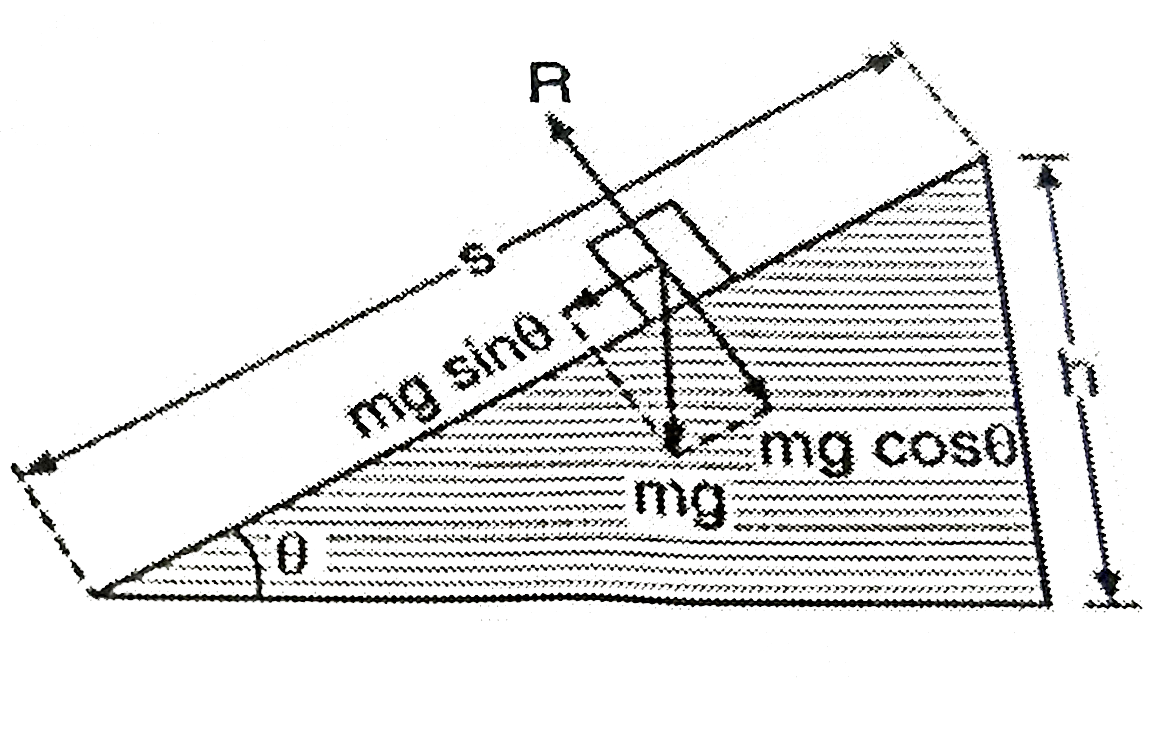
View SolutionA body starting from rest slides on an inclined plane of lengths as shown in Calculate the time of descent and speed at the bottom. Find also
(a) distance covered in half the time of descent and
(b) time taken to cover half the distance
View SolutionA glass marble dropped from a certain height above the horizontal surface reaches the surface in time t and then continues to bounce up and down. The time in which the marble finally comes to rest is
View SolutionA thin rim of mass m and radius r rolls down an inclined plane of slope α, winding thereby a thin ribbon of linear denstiy ρ (Fig). At the initial moment, the rim is at a height h above the horizontal surface. Determine the distance s from the foot of the inclined plane at which the rim stops, assuming that the inclined plane smoothly changes into the horizontal plane.

View SolutionA small mass slides down an inclined plane of inclination θ with the horizontal. The co-efficient of friction is μ=μ0 x where x is the distance through which the mass slides down and μ0 a constant. Then, the distance covered by the mass before it stops is
View Solution
