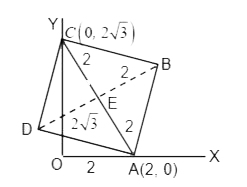
One diagonal of a square is the portion of the line $\sqrt{3} x + y = 2 \sqrt{3}$ intercepted by the axes. Obtain the extremities of the other diagonal is

A

$(1 + \sqrt{3}, \sqrt{3} - 1)$

B

$(1 + \sqrt{3}, - \sqrt{3} + 1)$

C

$(1 - \sqrt{3}, \sqrt{3} - 1)$

D

$(1 - \sqrt{3}, \sqrt{3} + 1)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Clearly, $O A = 2, O C = 2 \sqrt{3} ∴ E = (1, \sqrt{3})$ .
Also, $A C = \sqrt{2^{2} + 2 {(\sqrt{3})}^{2}} = 4 ∴ E B = E D = \frac{1}{2} A C = 2$
.m. of $A C = - \sqrt{3}$
$∴ .m. of B D = \frac{1}{\sqrt{3}} = {tan 30}^{\circ}$
$∴ B or D = (1 \pm 2 . {cos 30}^{\circ}, \sqrt{3} \pm 2 . {sin 30}^{\circ})$ .

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-JEE MAIN - 5-PART III : MATHEMATICS (SECTION-2)

Home
Ask Doubt
Profile