Find MI of a triangular lamina of mass M about the axis of rotation AB shown in Fig.

(ma2+b224)
m.a2b26(a2+b2)
m.a2b212(a2+b2)
(ma2+b212)
The correct Answer is:B
M.I. of rectangle =2(M. I. of triangle).
Consider a rod element of length l and width dx 1x=ba⇒1=bax
mass of element dm=mab1.dx=mab(bax)dx=ma2xdx
M.I. of the rod
dI=(dm)I23sin2θ=(ma2×dx)b2x2a2.sin2θ3=mb23a4sin4θx3dx

I=∫(dI)=mb23a4sin2θ∫a0x3dx=mb212.a2a2+b2, M.I of rectangular plate = 2I=ma2b26(a2+b2)
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 2 (Torque, Fixed and Rotation)
10 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 2 (General rigid body motion, Rolling)
10 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Mixed Numerical Questions)
15 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
A uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View Solutionif the earth is treated as a sphere of radius R and mass M, Its angular momentum about the axis of its rotation with period T, is
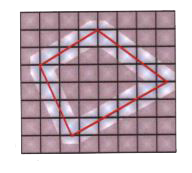
View SolutionFind the approximate area of an irregular lamina of which boundary line is drawn on the graph paper shown in Fig.
View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View SolutionThe moment of inertia of a cylinder of mass 1000gm and radius 20cm about the axis AB shown in figure is

View Solution
In the adjacent figure ABC is a uniform isosceles triangular lamina of mass m and AB=AC=l the lamina is free to rotate about a fixed horizontal axis OAO′ which is in the plane of the lamina. Initially the lamina is in static equilibrium with maximum gravitational potential energy. due to slight disturbance, lamina starts rotating. Now choose the correct option(s)
View SolutionThree rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.

View SolutionMoment of inertia of an equilateral triangular lamina ABC, about the axis passing through its centre O and perpendicular to its plane is I0 as shown in the figure. A cavithy DEF is cut out from the lamina, where D,E,F are the mid points of the sides. Moment of inertia of the remaining part of lamina about the same axis is -
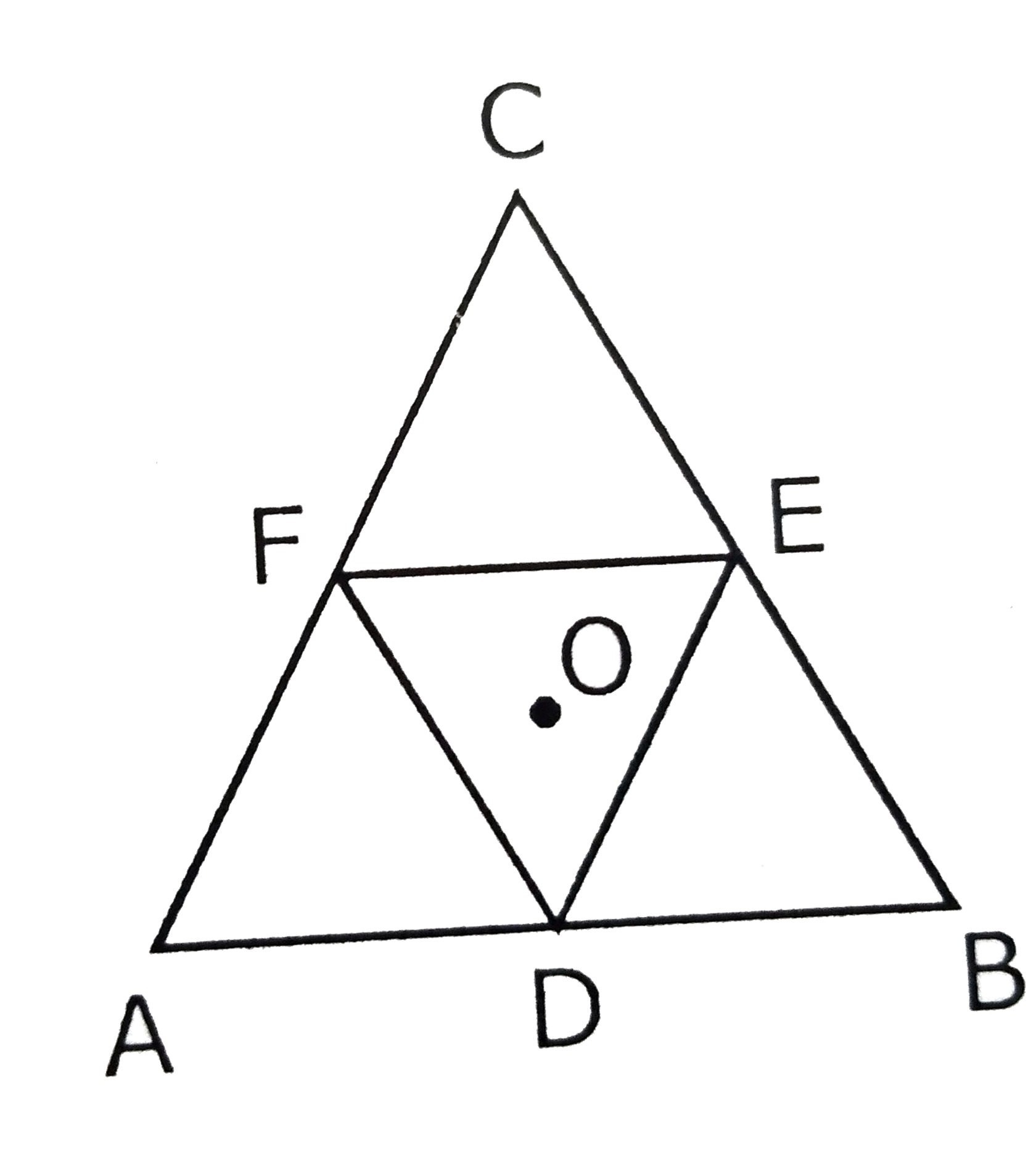
View SolutionMoment of inertia of an equilateral triangular lamina ABC, about the axis passing through its centre O and perpendicular to its plane is I0 as shown in the figure. A cavithy DEF is cut out from the lamina, where D,E,F are the mid points of the sides. Moment of inertia of the remaining part of lamina about the same axis is -

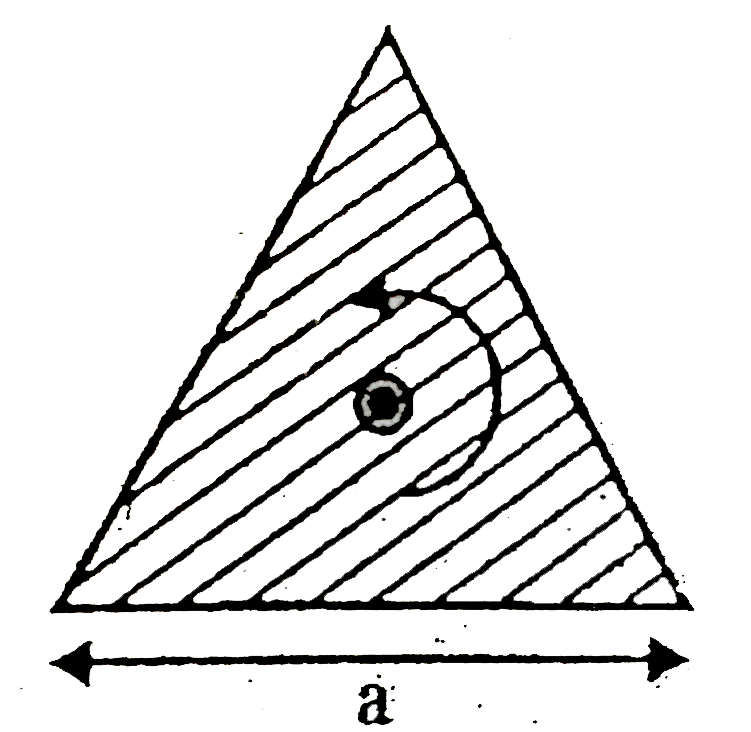
View SolutionA uniform equilateral triangular lamina of side a has mass m. Its moment of inertia about the axis passing through the centroid and prependicular to the plane of the lamina is :-
View Solution
