In Fig. the velocities are in ground frame and the cylinder is performing pure rolling on the plank, velocity of point $' A'$ would be

A

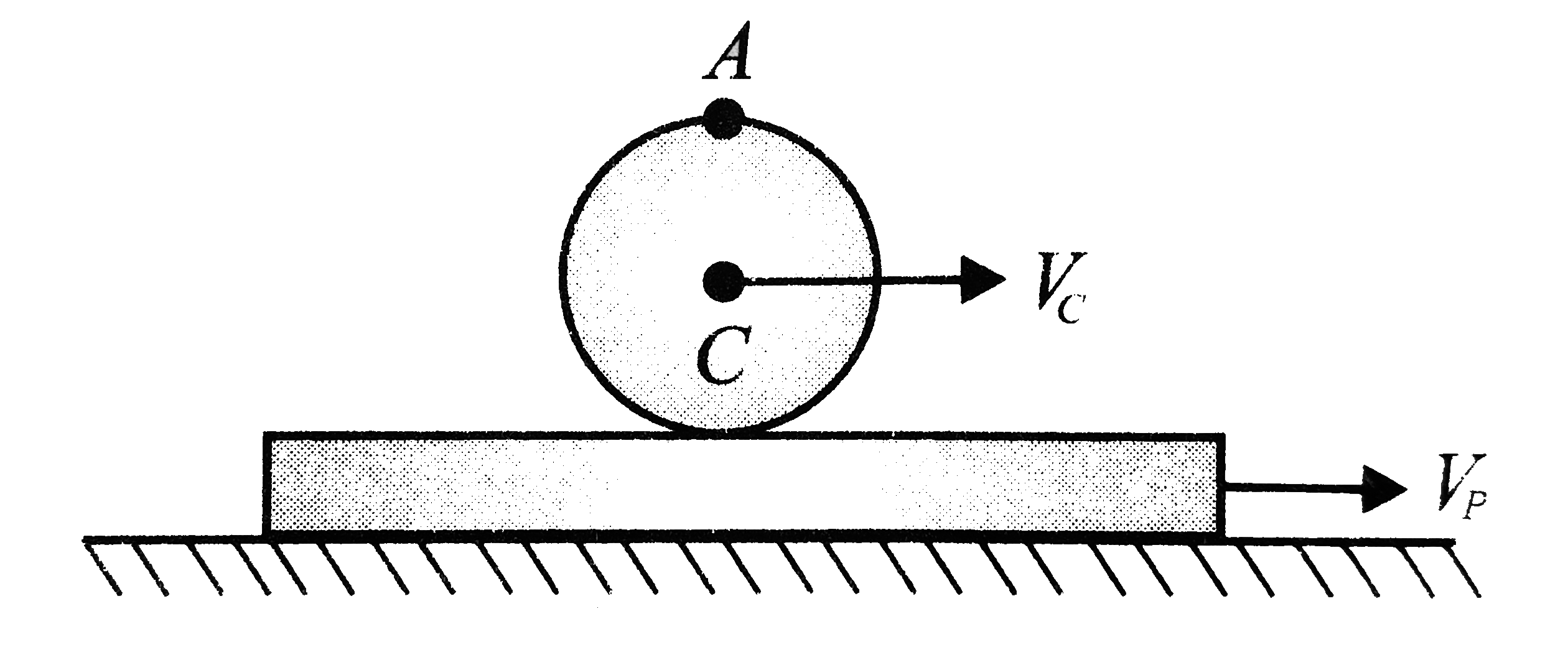
$2 V_{c}$

B

$2 V_{c} + V_{P}$

C

$2 V_{c} - V_{P}$

D

$2 (V_{c} - V_{p})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

For pure rollig velocity of the point of contct has to be equal to the velocity of the surface.
let's say cylinder rolls with angular velocity $ω$ : At bottom most point,
$V_{C} - ω r = V_{P} \Rightarrow ω r = V_{C} - V_{P}$
At top most point
$V_{A} = V_{C} + ω r = 2 V_{C} - V_{P}$

Updated on:21/07/2023

|

Class 12 PHYSICS ROTATIONAL MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

A system of identical cylinders and plates is shown in Fig. All the cylinders are identical and there is no slipping at any contact. The velocity of lower and upper plates are $V$ and $2 V$ , respectively, as shown in Fig. Then the ratio of angular speeds of the upper cylinders to lower cylinders is

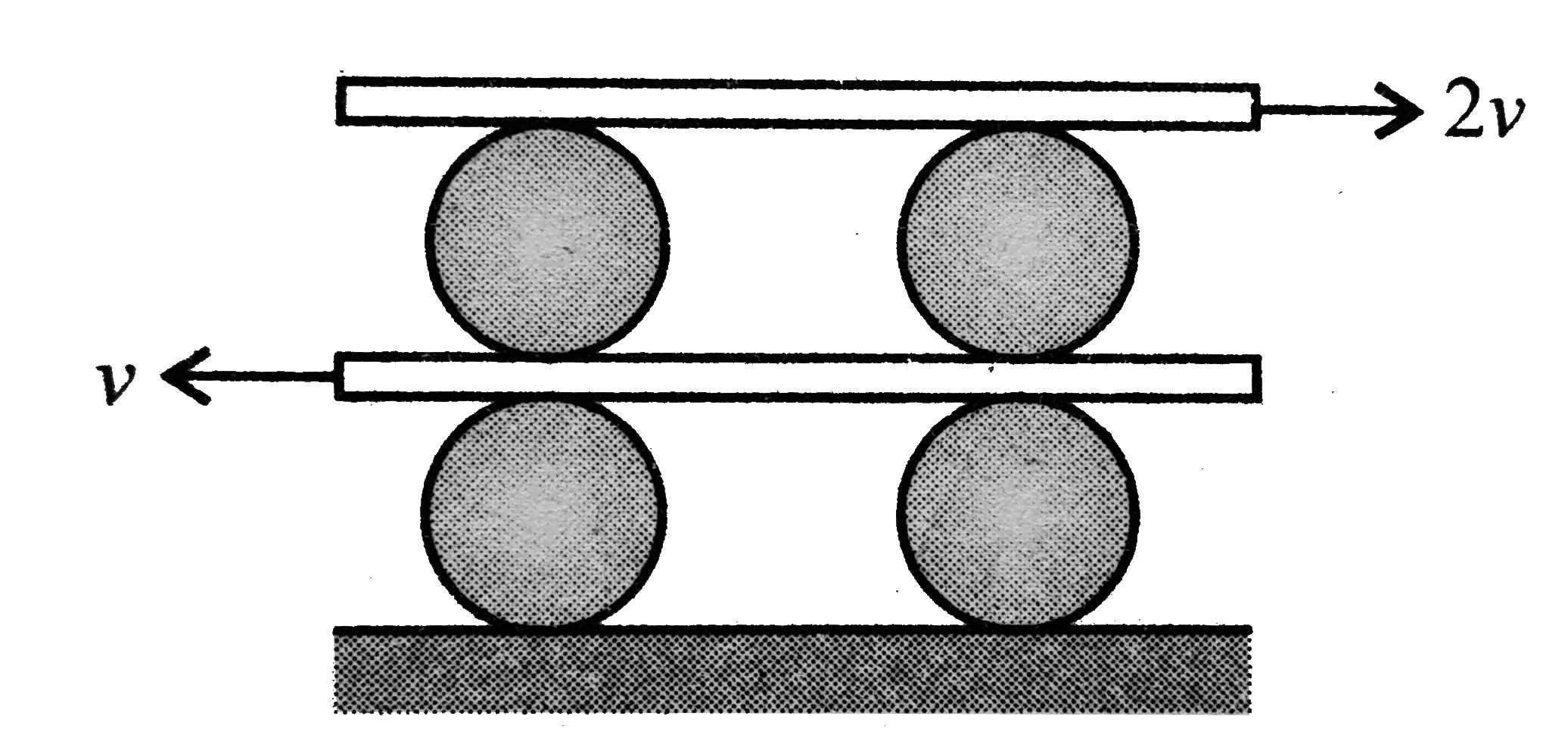A $1 : 3$
B $3 : 1$
C $1 : 2$
D $2 : 1$

VMC MODULES ENGLISH-ROTATIONAL MOTION -LEVEL - 1 (Mixed topics)

Home
Ask Doubt
Profile