A fuse wire melts when a currentIm is passed through it. The value of Im can be increased by:
[Assume that each change is made while keeping the other quantities fixed]
Decreasing the resistivity of the wire
Decreasing the area of cross-section of the wire
Increasing the resistivity of the wire
Increasing the melting point of the wire
To solve the problem of how to increase the melting current Im of a fuse wire, we can analyze the relationship between current, resistance, and resistivity. Here’s a step-by-step breakdown:
Step 1: Understand the relationship between current, voltage, and resistance
The current Im that causes the fuse wire to melt can be expressed using Ohm's law:
Im=VR
where V is the voltage across the fuse wire and R is the resistance of the wire.
Step 2: Express resistance in terms of resistivity
Resistance R can be expressed in terms of resistivity ρ, length L, and cross-sectional area A:
R=ρLA
Step 3: Analyze the effect of changing resistivity
1. Decreasing the resistivity (ρ):
- If we decrease ρ, then R decreases (since R is directly proportional to ρ).
- As R decreases, Im increases (since Im is inversely proportional to R).
- Conclusion: This option increases Im.
Step 4: Analyze the effect of changing the area of cross-section
2. Decreasing the area (A):
- If we decrease A, then R increases (since R is inversely proportional to A).
- As R increases, Im decreases.
- Conclusion: This option decreases Im.
Step 5: Analyze the effect of increasing resistivity
3. Increasing the resistivity (ρ):
- If we increase ρ, then R increases.
- As R increases, Im decreases.
- Conclusion: This option decreases Im.
Step 6: Analyze the effect of changing the melting point
4. Decreasing the melting point:
- The melting point of the wire does not affect the current directly.
- Conclusion: This option does not have a relevant effect on Im.
Final Conclusion
The only option that increases the melting current Im is decreasing the resistivity of the wire.
Answer
The value of Im can be increased by decreasing the resistivity of the wire.
---
The current Im that causes the fuse wire to melt can be expressed using Ohm's law:
Im=VR
where V is the voltage across the fuse wire and R is the resistance of the wire.
Resistance R can be expressed in terms of resistivity ρ, length L, and cross-sectional area A:
R=ρLA
1. Decreasing the resistivity (ρ):
- If we decrease ρ, then R decreases (since R is directly proportional to ρ).
- As R decreases, Im increases (since Im is inversely proportional to R).
- Conclusion: This option increases Im.
2. Decreasing the area (A):
- If we decrease A, then R increases (since R is inversely proportional to A).
- As R increases, Im decreases.
- Conclusion: This option decreases Im.
3. Increasing the resistivity (ρ):
- If we increase ρ, then R increases.
- As R increases, Im decreases.
- Conclusion: This option decreases Im.
4. Decreasing the melting point:
- The melting point of the wire does not affect the current directly.
- Conclusion: This option does not have a relevant effect on Im.
The only option that increases the melting current Im is decreasing the resistivity of the wire.
The value of Im can be increased by decreasing the resistivity of the wire.
Topper's Solved these Questions
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-2
10 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-3
10 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 DAILY TUTORIAL SHEET -5
15 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
Similar Questions
An aluminium wire 7.5m long is connected in parallel with a copper wire 6m long. When a current of 5A is passed through the combination, it is found that the current in the aluminium wire is 3A. The diameter of the aluminium wire is 1mm. Determine the diameter of the copper wire. Resistivity of copper is 0.017μΩ−m and that of the aluminium is 0.028μΩ−m.
View SolutionA wire of cross-sectional area A forms three sides of a square and is free to rotate about axis OO'. If the structure is deflected by an angle θ from the vertical when current i is passed through it in a magnetic field B acting vertically upward and density of the wire is ρ, then the value of θ is given by

View SolutionA wire of cross-sectional area A forms three sides of a square and is free to rotate about axis OO'. If the structure is deflected by an angle θ from the vertical when current i is passed through it in a magnetic field B acting vertically upward and density of the wire is ρ, then the value of θ is given by

View SolutionIf the current I through a resistor is increased by 100% (assume that temperature remains unchanged), the increase in power dissipated will be :
View SolutionA current i passes through a wire of length l , radius of cross-section r and resistivity ρ . The rate of heat generation is
View SolutionA loosely wound helix made of stiff metal wire is mounted vertically with the lower end just touching the mercury in a dish. When the current from a battery is started in the metal wire through the mercury. then the spring
View SolutionA dc ammeter and a hot wire ammeter are connected to a circuit in series. When a direct current is passed through circuit, the dc ammeter shows 6 A. When ac current flows through circuit, the ac ammeter shows 8A. What will be reading of each ammeter if dc and ac current flow simulataneously through the circuit?
View Solution(A) : A helical spring tends to contract, when a current passes through it
(R) : Two straight parallel metallic wires carrying current in same direction repel each other
View SolutionA current of I amperes is flowing through each of the bent wires as shown. Find the magnitude of magnetic field at O.
View SolutionAssertion (A) A wire bent into an irregular shape with the point P and Q fixed . If a current I passed through the Wire, then the area enclosed by the irregular portion of the Wire increases.
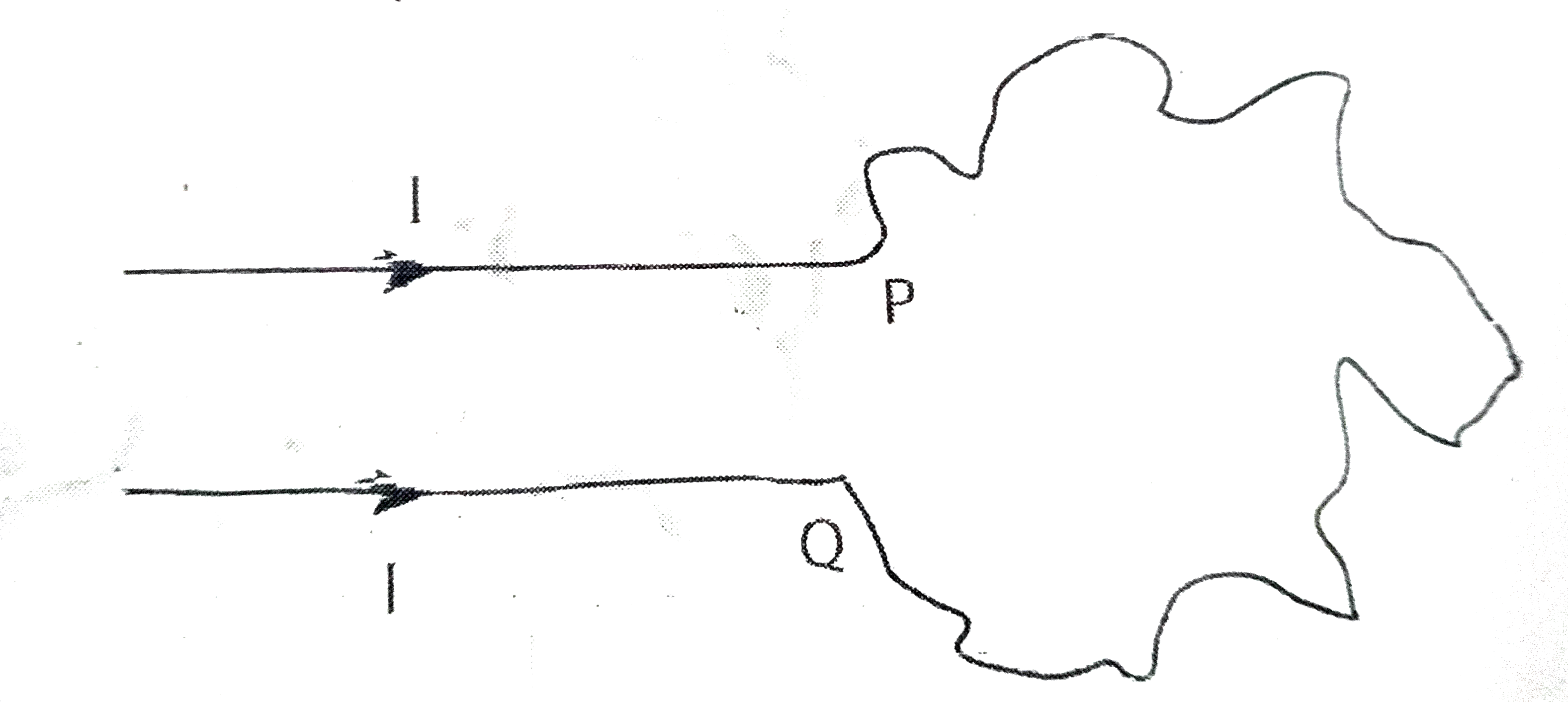
Reason (R ) Opposite currents carrying Wires repel each other.
View Solution
