If the solenoid in the above question is free to turn about the vertical direction, and a uniform horizontal magnetic field of 0⋅25T is applied, what is the magnitude of the torque on the solenoid when its axis makes an angle of 30∘ with the direction of the applied field?
To find the magnitude of the torque on the solenoid when it is subjected to a uniform horizontal magnetic field, we can follow these steps:
Step 1: Understand the Torque Formula
The torque (τ) experienced by a magnetic moment (M) in a magnetic field (B) is given by the formula:
τ=M⋅B⋅sin(θ)
where:
- τ is the torque,
- M is the magnetic moment,
- B is the magnetic field strength,
- θ is the angle between the magnetic moment and the magnetic field.
Step 2: Identify Given Values
From the problem statement, we have:
- Magnetic moment, M=0.6J/T
- Magnetic field strength, B=0.25T
- Angle, θ=30∘
Step 3: Calculate sin(θ)
We need to calculate sin(30∘):
sin(30∘)=12
Step 4: Substitute Values into the Torque Formula
Now, we can substitute the values into the torque formula:
τ=M⋅B⋅sin(θ)=0.6J/T⋅0.25T⋅12
Step 5: Perform the Calculation
Calculating the above expression step by step:
1. Calculate 0.6⋅0.25:
0.6⋅0.25=0.15
2. Now multiply by 12:
0.15⋅12=0.075
Step 6: Final Result
Thus, the magnitude of the torque on the solenoid is:
τ=0.075J
Summary
The magnitude of the torque on the solenoid when its axis makes an angle of 30∘ with the direction of the applied field is 0.075J.
---
The torque (τ) experienced by a magnetic moment (M) in a magnetic field (B) is given by the formula:
τ=M⋅B⋅sin(θ)
where:
- τ is the torque,
- M is the magnetic moment,
- B is the magnetic field strength,
- θ is the angle between the magnetic moment and the magnetic field.
From the problem statement, we have:
- Magnetic moment, M=0.6J/T
- Magnetic field strength, B=0.25T
- Angle, θ=30∘
We need to calculate sin(30∘):
sin(30∘)=12
Now, we can substitute the values into the torque formula:
τ=M⋅B⋅sin(θ)=0.6J/T⋅0.25T⋅12
Calculating the above expression step by step:
1. Calculate 0.6⋅0.25:
0.6⋅0.25=0.15
2. Now multiply by 12:
0.15⋅12=0.075
Thus, the magnitude of the torque on the solenoid is:
τ=0.075J
The magnitude of the torque on the solenoid when its axis makes an angle of 30∘ with the direction of the applied field is 0.075J.
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 0 ( SHORT ANSWER TYPE-II )
13 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 0 (LONG ANSWER TYPE )
3 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- MOCK TEST 1BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
Similar Questions
What is the magnitude of the magnetic force per unit length on a wire carrying a current of 8 A making an angle of 30∘ with the direction of a uniform magnetic field of 0⋅15T?
View SolutionWhat is the magnitude of the magnetic force per unit length on a wire carrying a current of 8 A making an angle of 30∘ with the direction of a uniform magnetic field of 0⋅15T?
View Solution
Knowledge Check
If a solenoid is free to turn about the vertical direction, and a uniform horizontal magnetic field of 0⋅25T is applied, what is the magnitude of the torque on the solenoid when its axis makes an angle of 30∘ with the direction of the applied field? Magnetic moment is 0.6JT−1
A0.075NmB0.080NmC0.081NmD0.091NmA uniform horizontal magnetic field of 7.5×10−2T is set up at an angle of 30∘ with the axis of an solenoid and the magnetic moment associated with it is 1.28JT−1. Then the torque on it is
A4.8×10−2NmB1.6×10−2NmC1.2×10−2NmD4.8×10−4NmA circular coil of 70 turns and radius 5 cm carrying a current of 8 A is suspended vertically in a uniform horizontal magnetic field of magnitude 1.5 T. The field lines make an angle of 30∘ with the normal of the coil then the magnitude of the counter torque that must be applied to prevent the coil from turning is
A33 NmB3.3 NmC3.3×10−2NmD3.3×10−4Nm
A long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
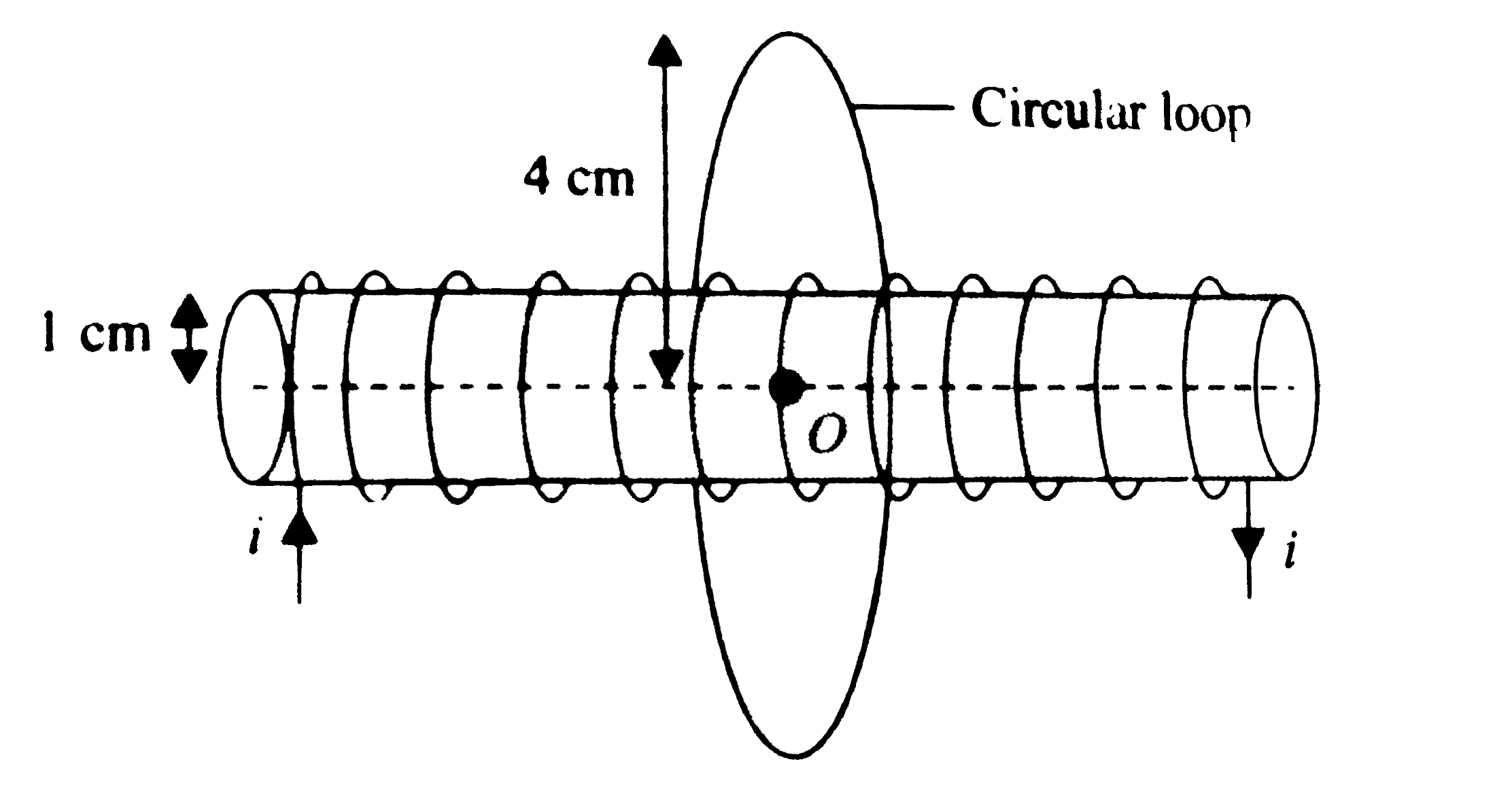
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
View SolutionA coil of 100 turns and area 5 square centimetre is placed in a magnetic field B = 0.2 T . The normal to the plane of the coil makes an angle of 60∘ with the direction of the magnetic field. The magnetic flux linked with the coil is
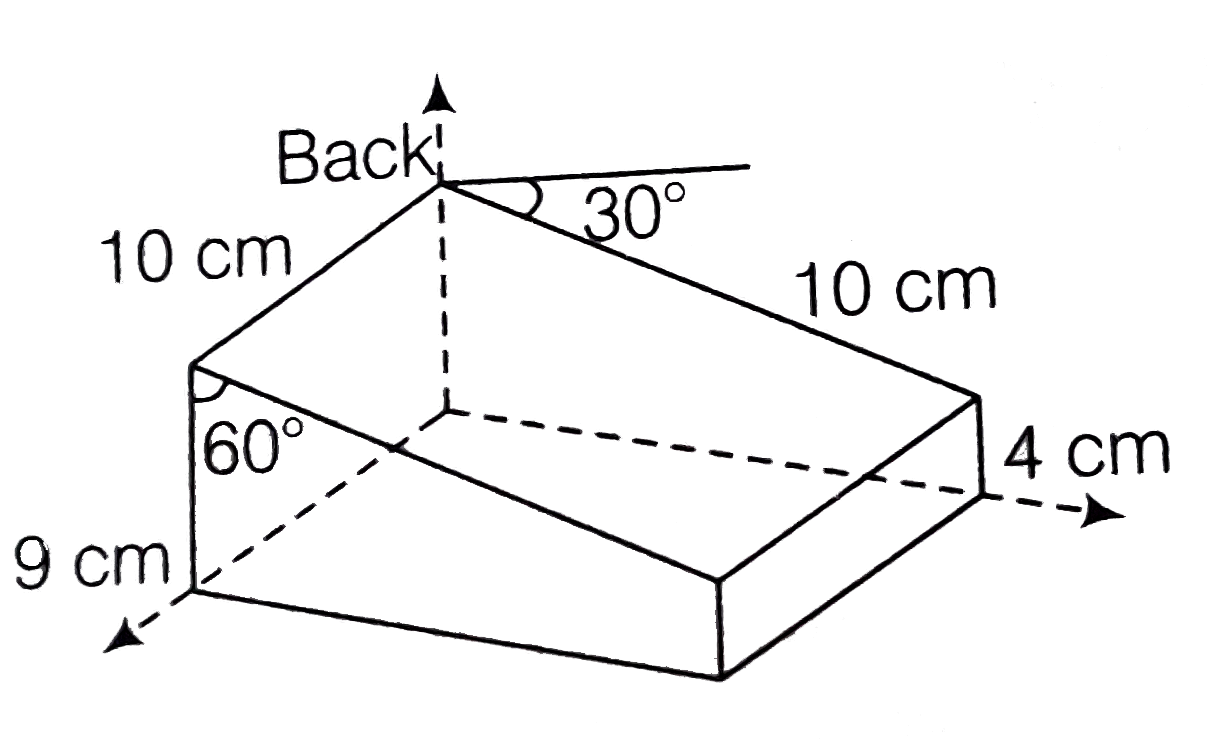
View SolutionConsider the following figure, a uniform magnetic field of 0.2 T is directed along the positive X-axis. The magnetic flux through top surface of the figure.
View SolutionWhy a thick metal plate oscillating about a horizontal axis stops when a strong magnetic field is applied on the plane?
View SolutionCompare the direction of the magnetic field inside a solenoid with that of the field there if the solenoid is replaced by its equivalent combination of north pole and south pole.
View Solution
