The position of a particle executing SHM is given by A sin(wt) Write the expression for the velocity of the particle.
To find the expression for the velocity of a particle executing simple harmonic motion (SHM) given its position as x(t)=Asin(ωt), we can follow these steps:
1. Identify the Position Function:
The position of the particle in SHM is given by:
x(t)=Asin(ωt)
where A is the amplitude and ω is the angular frequency.
2. Differentiate the Position Function:
To find the velocity, we need to differentiate the position function with respect to time t. The velocity v(t) is defined as:
v(t)=dxdt
3. Apply the Chain Rule:
Using the chain rule for differentiation, we differentiate Asin(ωt):
v(t)=Addt(sin(ωt))
4. Differentiate the Sine Function:
The derivative of sin(θ) with respect to θ is cos(θ). Therefore:
ddt(sin(ωt))=ωcos(ωt)
(Here, we also multiply by ω due to the chain rule since θ=ωt).
5. Combine the Results:
Substituting back into the expression for velocity, we get:
v(t)=A⋅ω⋅cos(ωt)
6. Final Expression for Velocity:
Thus, the expression for the velocity of the particle executing SHM is:
v(t)=Aωcos(ωt)
Summary:
The final expression for the velocity of the particle is:
v(t)=Aωcos(ωt)
The position of the particle in SHM is given by:
x(t)=Asin(ωt)
where A is the amplitude and ω is the angular frequency.
To find the velocity, we need to differentiate the position function with respect to time t. The velocity v(t) is defined as:
v(t)=dxdt
Using the chain rule for differentiation, we differentiate Asin(ωt):
v(t)=Addt(sin(ωt))
The derivative of sin(θ) with respect to θ is cos(θ). Therefore:
ddt(sin(ωt))=ωcos(ωt)
(Here, we also multiply by ω due to the chain rule since θ=ωt).
Substituting back into the expression for velocity, we get:
v(t)=A⋅ω⋅cos(ωt)
Thus, the expression for the velocity of the particle executing SHM is:
v(t)=Aωcos(ωt)
The final expression for the velocity of the particle is:
v(t)=Aωcos(ωt)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 SHORT ANSWER TYPE - I
8 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - LEVEL 0 SHORT ANSWER TYPE - II
12 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
Similar Questions
The displacement of a particle executing SHM is given by y=0.25 sin(200t) cm . The maximum speed of the particle is
View SolutionEnergy of particle executing SHM depends upon
View Solutiondisplacement versus time curve for a particle executing SHM is is as shown in figure. At what points the velocity of the particle is zero?
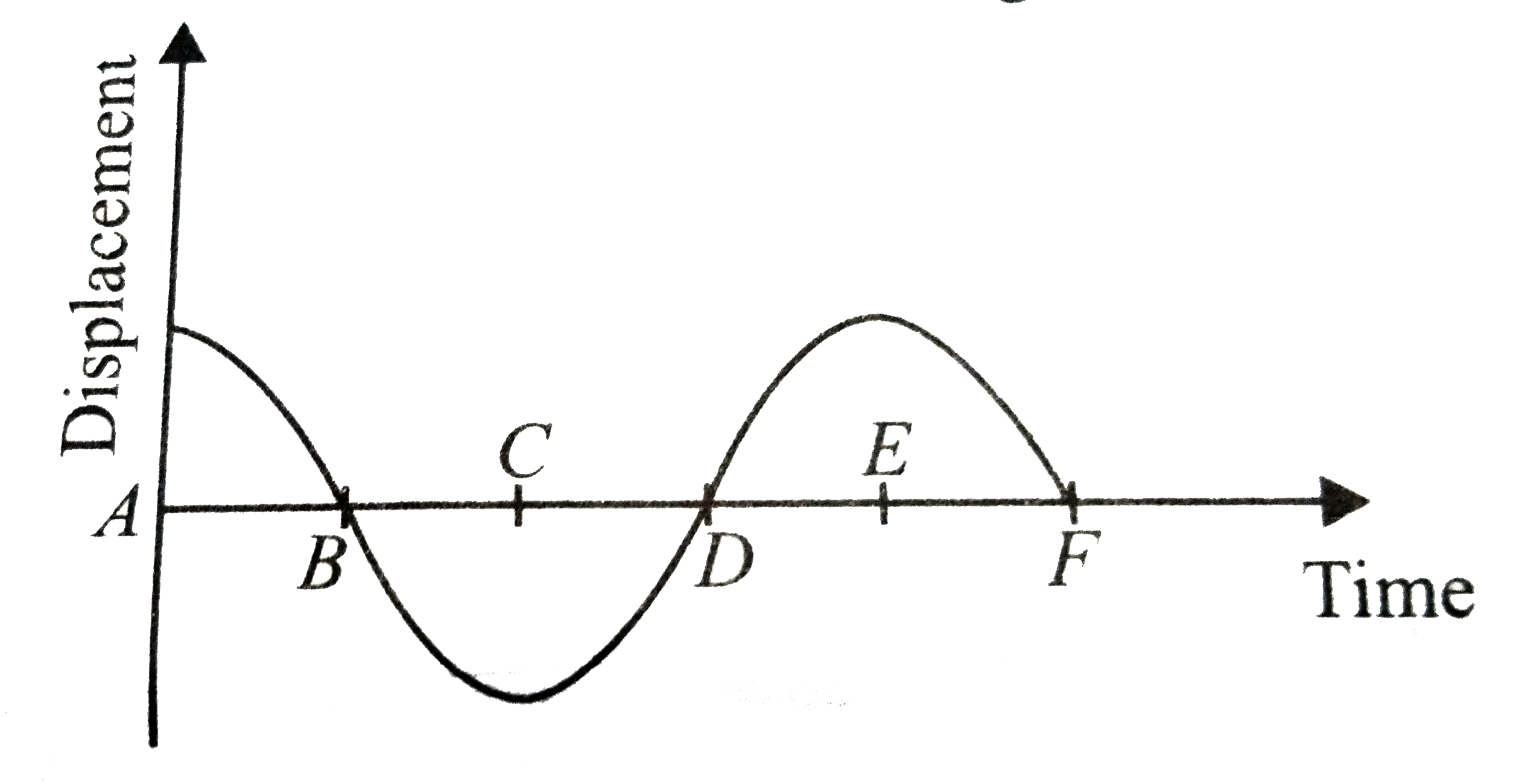
View Solution
The variation of velocity of a particle executing SHM with time is shown is fig. The velocity of the particle when a phase change of π6 takes place from the instant it is at one of the extreme positions will be
View SolutionThe displacement of a particle executing SHM is given by
y=0.5 sin100t cm . The maximum speed of the particle is
View SolutionThe amplitude of a particle executing SHM about O is 10cm. Then
View SolutionThe displacement-time graph of a particle executing SHM is as shown in the figure.

The corresponding force-time graph of the particle is
(a)
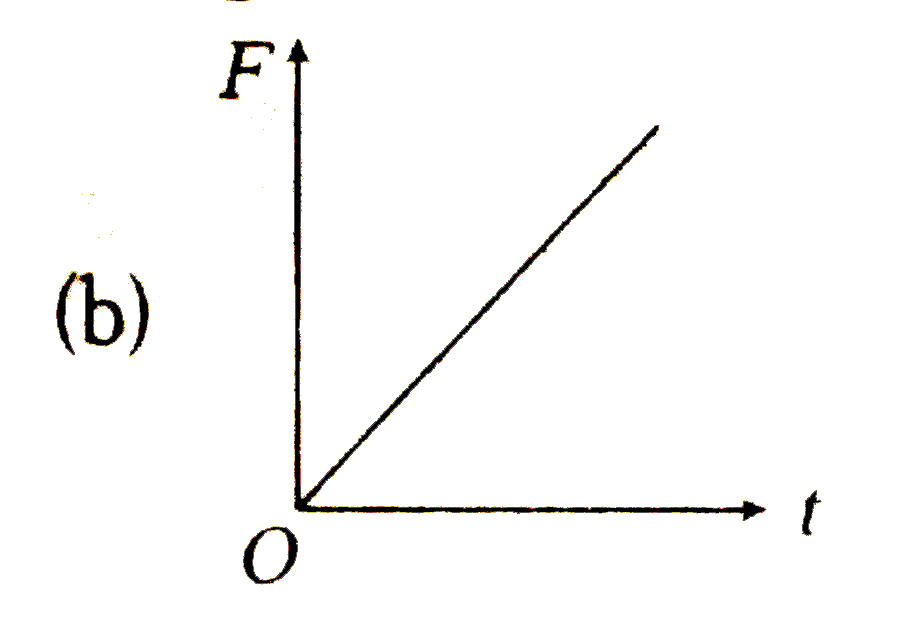
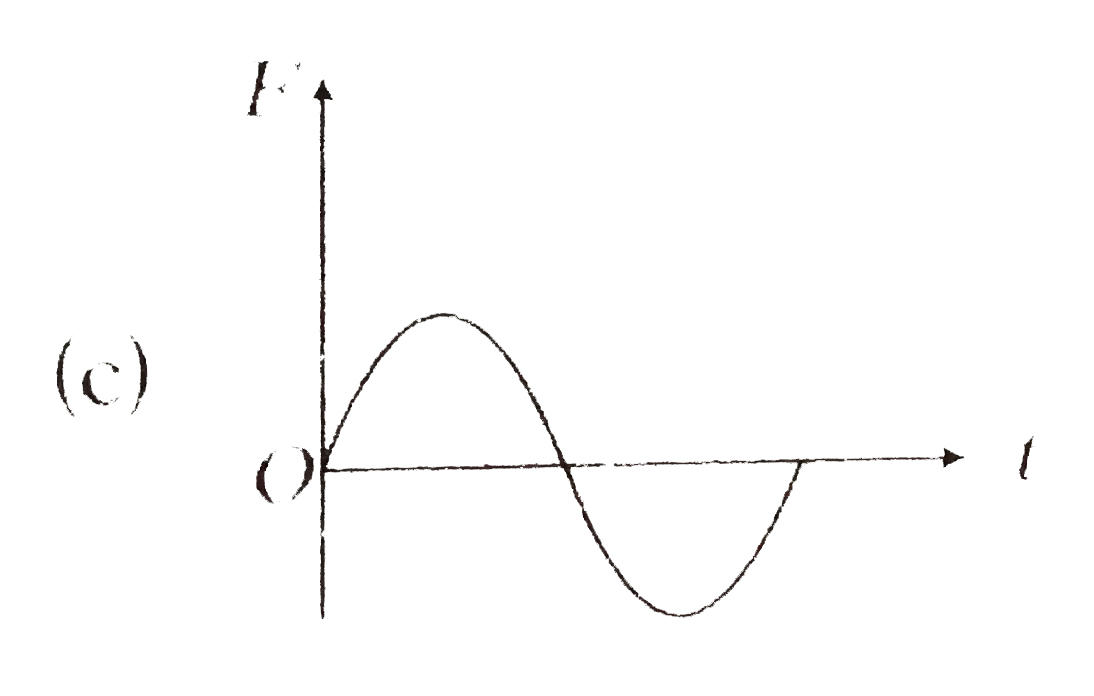
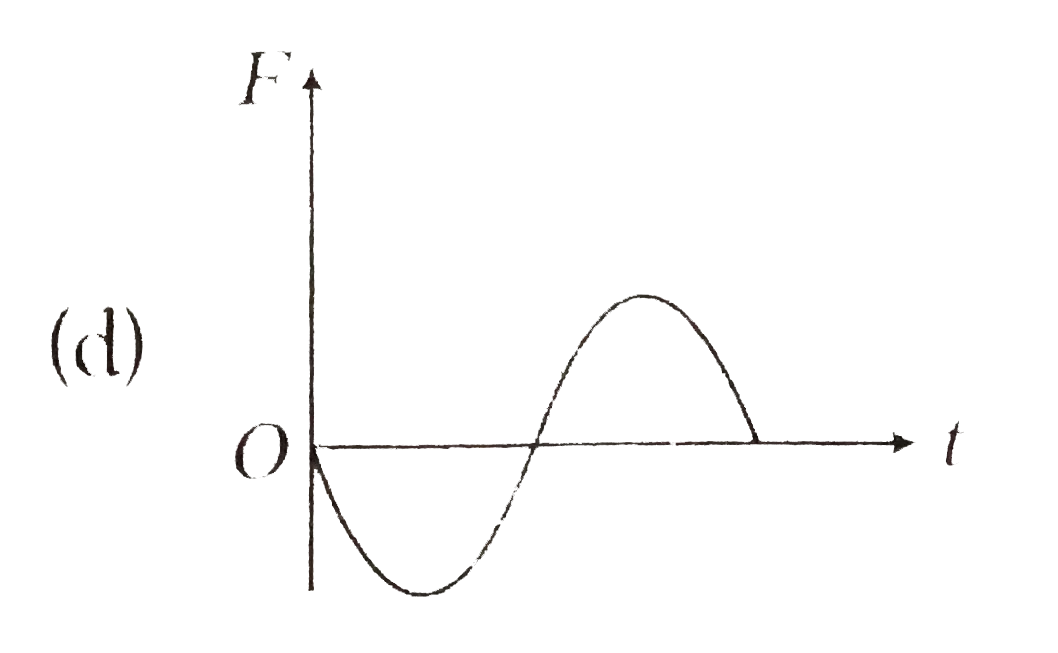
View SolutionVelocity at mean position of a particle executing SHM is v. Velocity of the particle at a distance equal to half of the amplitude will be
View SolutionIf the displacement (x) and velocity (v) of a particle executing SHM are related through the expression 3v2=30−x2. If the time period of the particle is T=π√n, then what is the value of n?
View SolutionThe potential energy of a particle executing SHM varies sinusoidally with frequency f. The frequency of oscillation of the particle will be
View Solution
