An artificial satellite of Earth nears the end of its life due to air resistance. While still in orbit:
It moves faster as the orbit lower
It moves slower as the orbit lowers
It slowly spirals away from Earth
It moves slower in the same orbit but with a decreasing period
The correct Answer is:A
To solve the question regarding the behavior of an artificial satellite nearing the end of its life due to air resistance while still in orbit, we can analyze the situation step by step.
1. Understanding the Scenario:
- An artificial satellite is in orbit around the Earth and is experiencing air resistance. This air resistance will affect its motion.
2. Effect of Air Resistance:
- As the satellite moves through the atmosphere, air resistance acts against its motion, causing it to lose altitude. This means the satellite will gradually spiral downwards towards Earth.
3. Conservation of Mechanical Energy:
- The mechanical energy of the satellite is the sum of its potential energy (due to its height above the Earth) and its kinetic energy (due to its speed). According to the conservation of energy, if the satellite loses potential energy (as it descends), its kinetic energy must increase to keep the total mechanical energy constant.
4. Potential Energy Decrease:
- As the satellite descends, its height decreases, leading to a decrease in potential energy. This is given by the formula PE=mgh, where m is mass, g is the acceleration due to gravity, and h is the height.
5. Kinetic Energy Increase:
- To maintain the conservation of mechanical energy, the decrease in potential energy must be compensated by an increase in kinetic energy. This is represented by the formula KE=12mv2, where v is the velocity of the satellite.
6. Conclusion about Velocity:
- Since the kinetic energy increases as the satellite descends, the velocity of the satellite must also increase. Therefore, as the orbit lowers, the satellite moves faster.
7. Choosing the Correct Option:
- Based on the analysis, the correct answer is that the satellite "moves faster as the orbit lowers."
Final Answer:
The correct option is: A) It moves faster as the orbit lowers.
- An artificial satellite is in orbit around the Earth and is experiencing air resistance. This air resistance will affect its motion.
- As the satellite moves through the atmosphere, air resistance acts against its motion, causing it to lose altitude. This means the satellite will gradually spiral downwards towards Earth.
- The mechanical energy of the satellite is the sum of its potential energy (due to its height above the Earth) and its kinetic energy (due to its speed). According to the conservation of energy, if the satellite loses potential energy (as it descends), its kinetic energy must increase to keep the total mechanical energy constant.
- As the satellite descends, its height decreases, leading to a decrease in potential energy. This is given by the formula PE=mgh, where m is mass, g is the acceleration due to gravity, and h is the height.
- To maintain the conservation of mechanical energy, the decrease in potential energy must be compensated by an increase in kinetic energy. This is represented by the formula KE=12mv2, where v is the velocity of the satellite.
- Since the kinetic energy increases as the satellite descends, the velocity of the satellite must also increase. Therefore, as the orbit lowers, the satellite moves faster.
- Based on the analysis, the correct answer is that the satellite "moves faster as the orbit lowers."
The correct option is: A) It moves faster as the orbit lowers.
Topper's Solved these Questions
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level-2
30 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Main (Archive)
43 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - LEVEL -0 Long Answer Type
3 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)
12 Videos
Similar Questions
An artificial satellite of the earth releases a packet. If air resistance is neglected, the point where the packet will hit, will be
View SolutionAn artificial satellite of the earth is launched in circular orbit in the equatorial plane of the earth and the satellite is moving from west to east. With respect to a person on the equator, the satellite is completing one round trip in 24h. Mass of the earth is M=6×1024kg.For this situation the orbital radius of the satellite is
View SolutionAn artificial satellite is orbiting around the earth with the speed of 4kms−1 at a distance of 104 km from the earth. Calculate its centripetal acceleration.
View SolutionFigure shows the path of a projectile thrown near the surface of earth in the absence of air resistance.
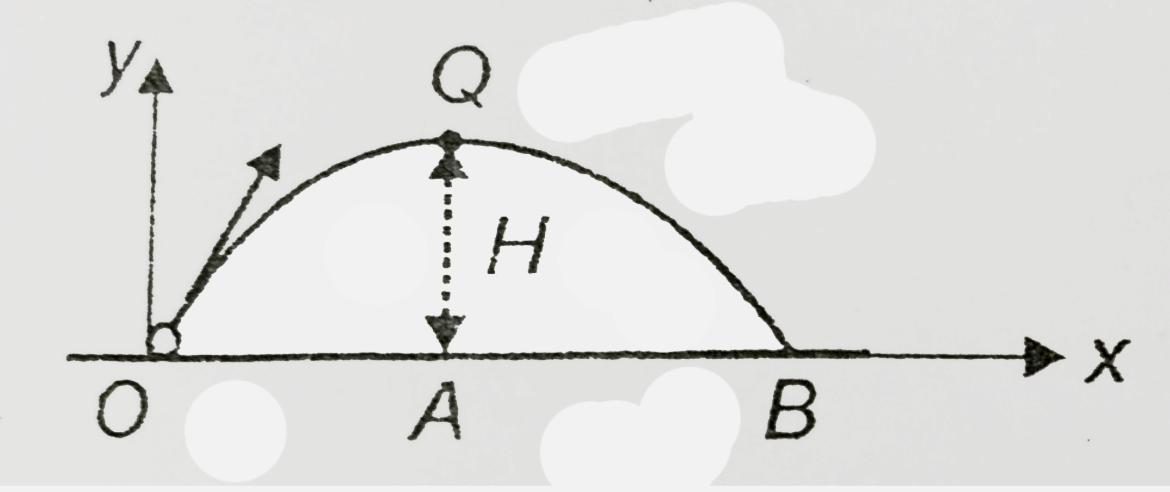
If the air resistances is taken into consideration , then
View SolutionAn artificial satellite in the presence of frictional forces will move into an orbit closer to the earth and may have increased kinetic energy. Explain this.
View SolutionThe orbital velocity of an artifical satellite in a cirular orbit above the earth's surface at a distance equal to radiu of earth is v. For a satellite orbiting at an altitude half of earth's radius, orbital velocity is
View SolutionWhat would happen to an artificial satellite, if its orbital velocity is slightly decreased due to some defects in it?
View SolutionShould the speed of two artificial satellites of the earth having the different masses but the same orbital radius be the same?
View SolutionStatement-1: The plane of the orbit of an artificial satellite must contain the centre of the Earth.
Statement-2: For an artificial satellite, the necessary centripetal force is provided by gravity.
View SolutionAn artificial satellite is made to move in circular orbits of different radii around the earth. The variations of its K.E., P.E. and total energy (E) in different orbits is shown in the figure by different curves. Then for the satellites
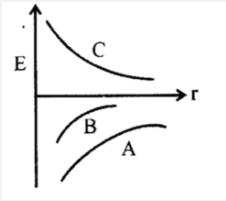
View Solution
