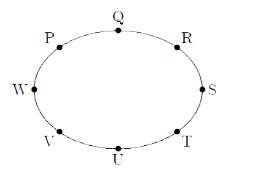
A planet travels in an elliptical orbit about a star as shown. At what pair of points is the speed of the planet the same?
(i) According to law of conservation of angular momentum L = mvr = constant, therefore the comet muses faster when it is close to the sun and moves slower when it is farther away from the sun. Therefore, the speed of the comet does not remain constant.
(ii) A the linear speed varies, the angular speed also varies. Therefore, angular speed of the comet does not remain constant
(iii) A no external torque is acting on the comet, therefore, according to law of conservation of angular momentum, the angular momentum of the comet remain constan.
(iv) As the linear speed of the comet changes its kinetic energy also changes. Therefore, its KE does not remain constant.
(v) Potential energy of the comet changes as its kinetic energy changes.
(vi) Only angular momentum and total energy of a comet remain constant throughout its orbit.
Topper's Solved these Questions
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - LEVEL -0 Long Answer Type
3 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level-1 MCQs
60 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - LEVEL -0 Short Answer Type – I
6 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)
12 Videos
Similar Questions
Knowledge Check
A planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at
 AABBCCDD
AABBCCDDA planet orbits the sun in an elliptical path as shown in the figure. Let vp and vA be spped of the planet when at perohelion and aphelion respectively. Which of the following relations is correct ?
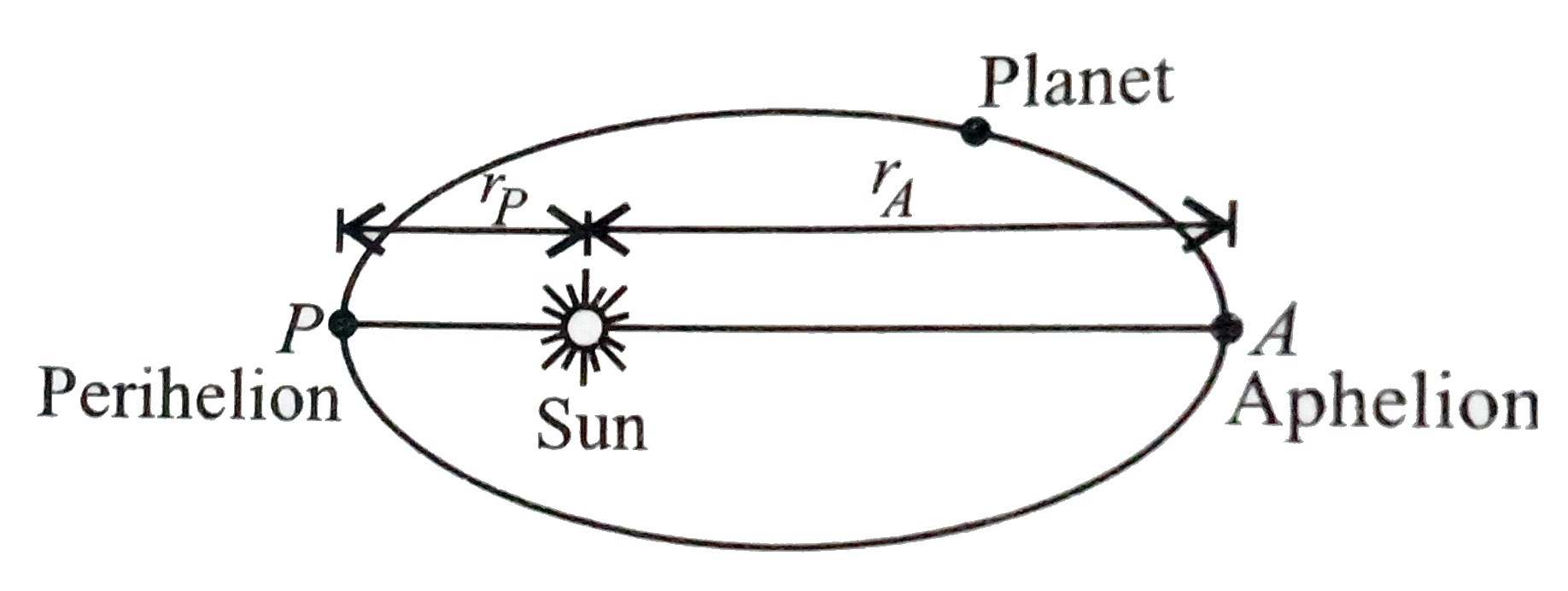 ArprA=vAvpBrprA=vpvACrprA=√vpvADrprA=√vAvp
ArprA=vAvpBrprA=vpvACrprA=√vpvADrprA=√vAvpA planet revolves around the sun in elliptical orbit of eccentricity 'e'. If 'T' is the time period of the planet then the time spent by the planet between the ends of the minor axis and major axis close to the sun is
ATπ2eBT(2eπ−1)CTe2πDT(14−e2π)
A planet of mass m is moving in an elliptical orbit about the sun (mass of sun = M). The maximum and minimum distances of the planet from the sun are r1 and r2 respectively. The period of revolution of the planet wil be proportional to :
View SolutionA planet is moving round the sun in an elliptical orbit as shows. As the planet moves from A to B

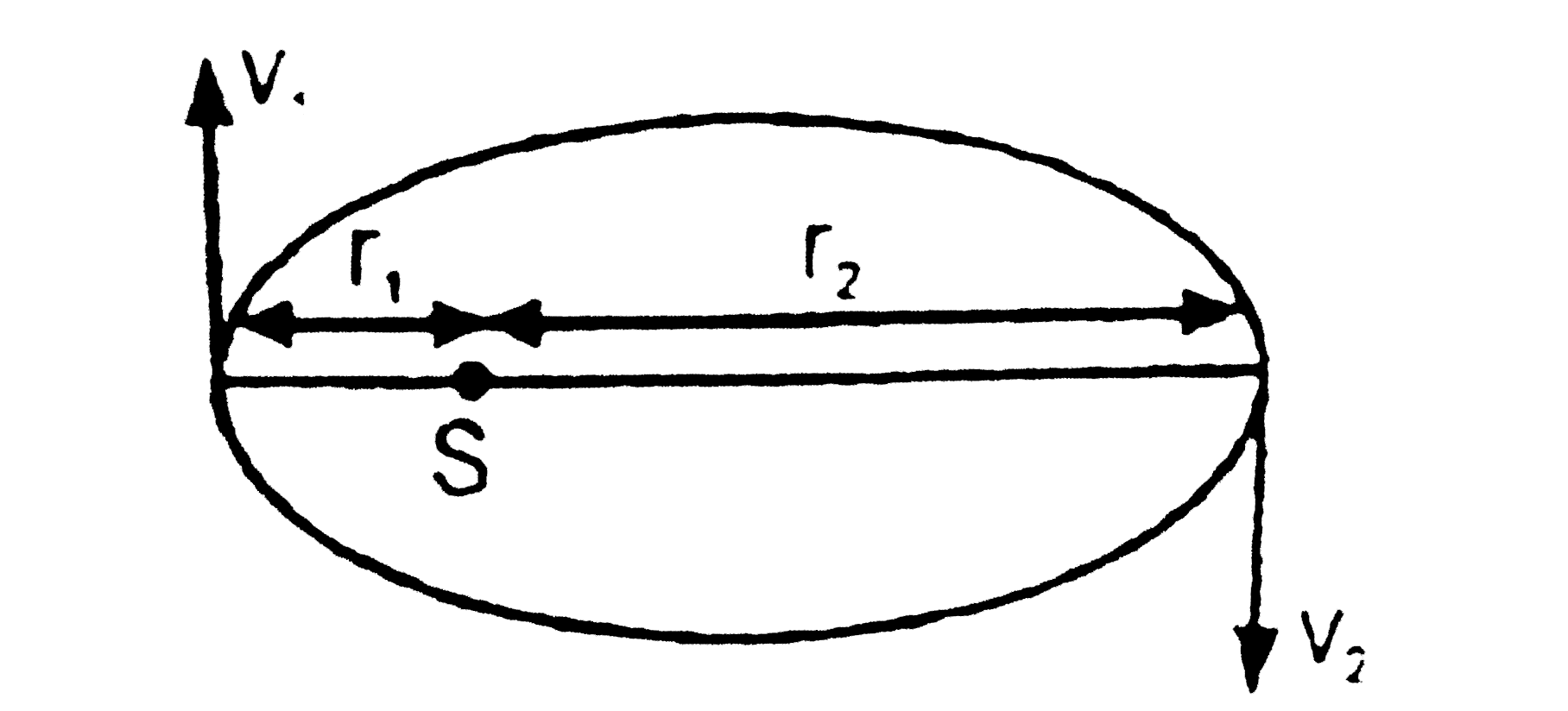
View SolutionA planet is revolving in an elliptical orbit around the sun as shown in the figure. The areal velocity (area swapped by the radius vector with respect to sun in unit time) is:
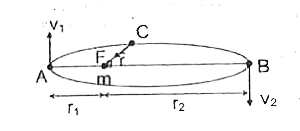
View SolutionIn the figure shown a planet moves in an elliptical orbit around the sun. Compare the speeds, linear and angular momenta at the points A and B.
View SolutionA planet of mass m is in an elliptical orbit about the sun (m << Msun) with an orbital period T. If A be the area of orbit, then its angular momentum would be:
View Solution
