A very long wire ABCDEFBDG is shown in figure carrying current I. AC and CG parts are straight, long and at right angle. At D wire forms a circular turn DEFBD of radius R. AC, CG parts are tangential to circular turn at B and D. Magnetic field at the centre of circle is:
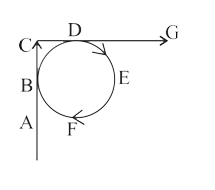
μ0IR
μ0I2πR(π+1)
μ0I2πR(π+1√2+1)
μ0I2πR(π−1√2)
The correct Answer is:C
We say we have 3 parts
B=BA+BB_+BC
=μ0I4πR(sin90∘+sin45∘)+μoI2R+μ0I4πR(sin45∘+sin90∘) =μ0I2πR(π+1√2+1)

Topper's Solved these Questions
- JEE MAIN REVISION TEST - 27 - JEE -2020BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 27 - JEE -2020EXERCISE - PHYSICS (SECTION 2)
5 Videos
- JEE MAIN REVISION TEST - 26 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 26 (2020)EXERCISE - PHYSICS (SECTION 2)
5 Videos
- JEE MAIN REVISION TEST - 28BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 28EXERCISE - PHYSICS (SECTION-2)
5 Videos
Similar Questions

A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius R
View SolutionIn the figure, the current l enters the circular loop of uniform wire of radius r at A and leaves it at B. The magnetic field of the centre of circular loop is

View SolutionA current I enters a uniform circular coil of radius R, branches into two parts and then recombines as shown in the circuit diagram. The resultant magnetic field at the centre of the coil is :
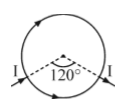
View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionA long wire bent as shown in fig. carries current I. If the radius of the semicircular portion is a, the magnetic field at centre C is

View SolutionB0 is the magnetic field at point P for a given straight wire as shown in figure. If this wirre is bent into a circular loop, then magnetic field at the centre of loop is
_PHY_E06_130_Q01.png)
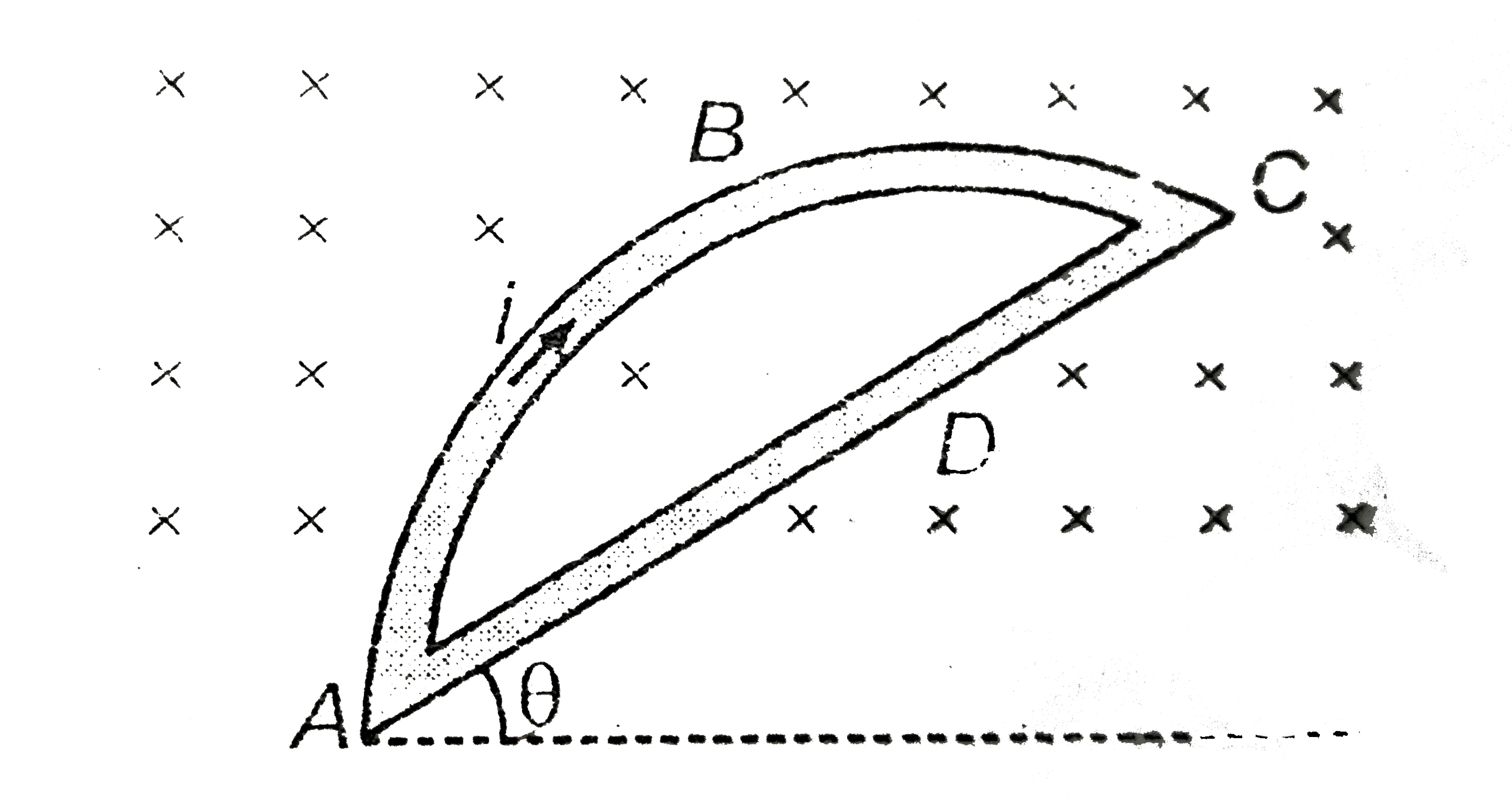
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

View SolutionA current carrying wire AB of the length L is turned along a circle, as shown in figure. The magnetic field at the centre O.

View SolutionA circular wire ABC and a straight conductor ADC are carrying current i and are kept in the magnetic field B then
View Solution
