
A circular disc of radius b has a hole of radius a at its centre (see figure) if the mass per unit area of the disc varies as (σ0r) then the radius of gyration of the disc about its axis passing through the centre is
a+b2
√a2+b2+ab2
√a2+b2+ab3
a+b3
The correct Answer is:C
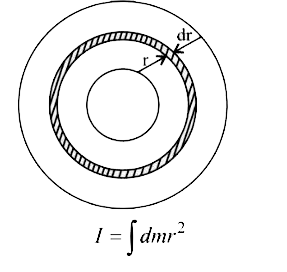
l=∫dmr2
⇒ ∫da(σ0r2πrdr)r2 ⇒ l=2σ0πb3(−a3)3 ⇒ l=mk2
⇒ 2σ0π(b3−a3)3=2σ0π(b−a)K2 ⇒ k=√a2+b2+ab3
Topper's Solved these Questions
- JEE MAIN REVISION TEST- 16BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST- 16EXERCISE - PHYSICS (SECTION 2)
5 Videos
- JEE MAIN REVISION TEST 8 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST 8 (2020)EXERCISE - PHYSICS (SECTION 2)
5 Videos
- JEE MAIN REVISION TEST- 24 BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST- 24 EXERCISE - PHYSICS ( SECTION - 2)
5 Videos
Similar Questions
Knowledge Check
From a uniform circular disc of radius R and mass 9M, a small disc of radius R3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
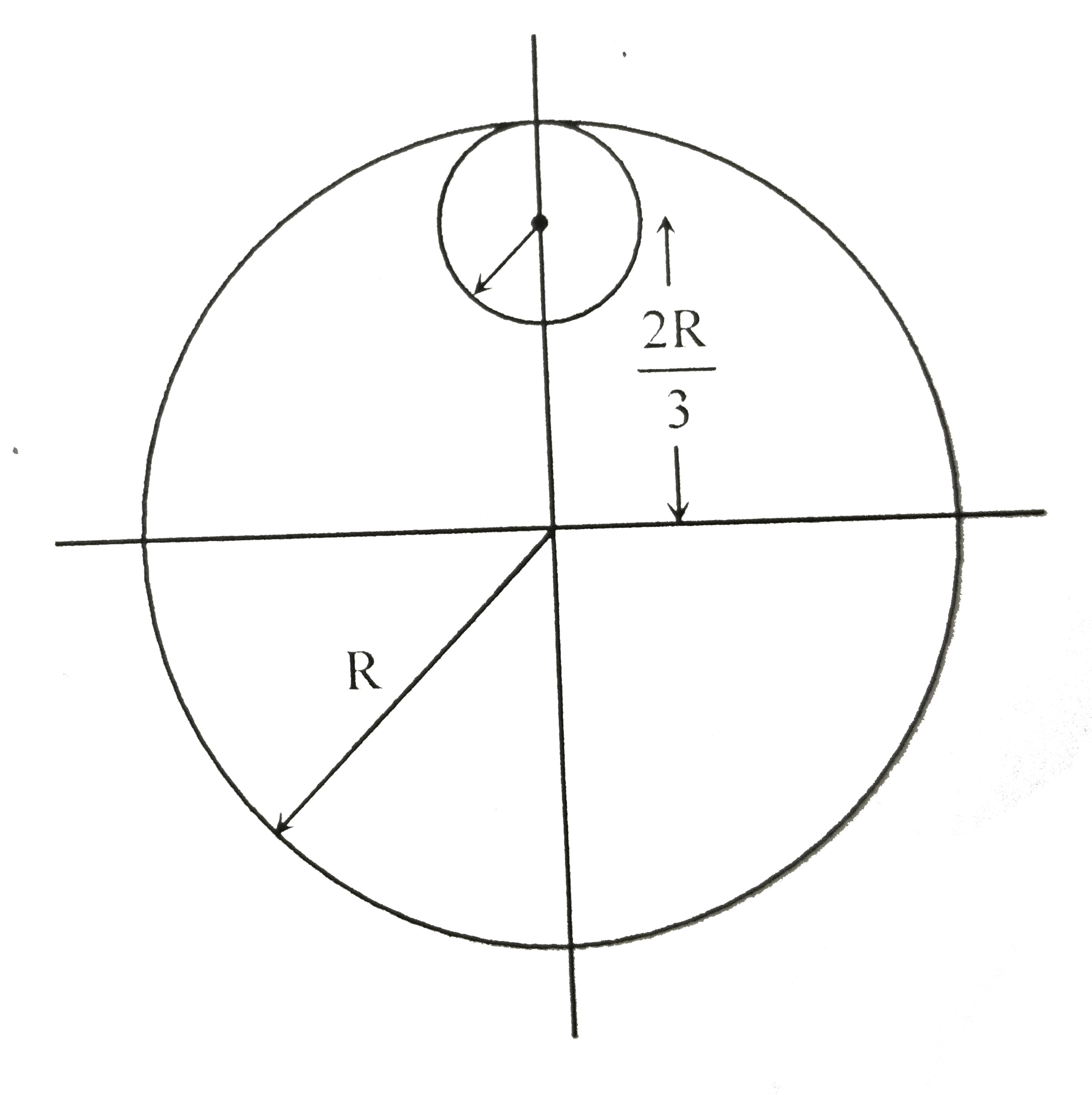 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2
Calculate the radius of gyration of a circular disc about its diameter.
View SolutionA uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
View SolutionFrom a disc of radius RandmassM, a circular hole of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of remaining part of the disc about a perependicular axis, passing through the centre ?
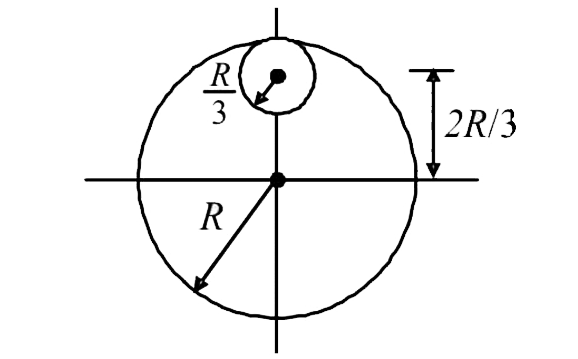
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −

View SolutionFrom the circular disc of radius 4R two small discs of radius R are cut off. The centre of mass of the new structure will be at
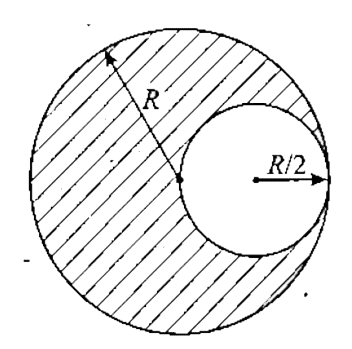
View SolutionMass per unit area of a disc of inner radius 'a' and outer radius 'b' is given by (σ0r),r distance from center. Its radius of gyration w.r.t. axis of rotation passing through center and perpendicular to plane is
View Solution
