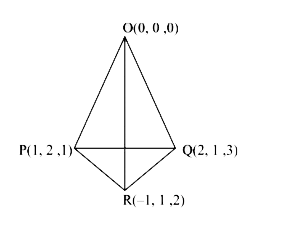
A tetrahedron has vertices O (0,0,0), A(1,2,1,), B(2,1,3) and C(-1,1,2), the angle between faces OAB and ABC will be

A

${cos}^{- 1} (\frac{9}{35})$

B

${cos}^{- 1} (\frac{17}{31})$

C

${cos}^{- 1} (\frac{7}{31})$

D

${cos}^{- 1} (\frac{19}{35})$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Vector perpendicular to face OPQ
$\to n_{1} = - - \to O P \times - - \to O Q = ∣ ∣ ∣ ∣ ∣ \begin{matrix} i & j & k 1 & 2 & 1 2 & 1 & 3 \end{matrix} ∣ ∣ ∣ ∣ ∣ = 5 i - j - 3 k$
Vector perpendicular to face PQR
$\to n_{2} = - - \to P Q \times - - \to P R = ∣ ∣ ∣ ∣ ∣ \begin{matrix} i & j & k - 2 & - 1 & 1 1 & - 1 & 2 \end{matrix} ∣ ∣ ∣ ∣ ∣ = - i + 5 j + 3 k$
$∴$ Angle between two faces is given by
$cos θ = ∣ ∣ ∣ \frac{- 5 - 5 - 9}{\sqrt{35} \sqrt{35}} ∣ ∣ ∣ = \frac{19}{35}$
$θ = {cos}^{- 1} (\frac{19}{35})$ .
.

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-JEE MAIN REVISION TEST 8 (2020)-MATHEMATICS ( SECTION 2 )

Home
Ask Doubt
Profile