If p.m.f. of r. v. X is given below.

then Var(x) = .......
A
p2
B
q2
C
pq
D
2pq
Video Solution
Text Solution
The correct Answer is:D
|
Answer
Step by step video, text & image solution for If p.m.f. of r. v. X is given below. then Var(x) = ....... by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II PROBABILITY DISTRIBUTIONS (II. Fill in the blanks)
7 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II PROBABILITY DISTRIBUTIONS (III. State whether each of the following is True or False.)
9 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II ASSIGNMENT PROBLEMS AND SEQUENCING (V. Activities)
2 Videos
- PROBABILITY DISTRIBUTIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
9 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CHOICE QUESTIONS
8 Videos
Similar Questions
Knowledge Check
The p.m.f. of a r.v. X is
P(x) =1/15, for x =1,2, .......... , 14,15
= 0 otherwise.
Then, E(X) is equal toA2B4C6D8The p.m.f. of a.r.v. X is as follows:
P(X=0)=3k3,P(X=1)=4k−10k2, P(X=2)=5k-1, P(X=x)=0 for any other value of x, then value of k isA13B23C1D2The p.m.f. of a r.v. X is P(x)={2xn(n+1)x=1,2,....,n0otherwise
Then E(X) =An+13B2n+13Cn−23D2n−13
The probability mass funciton (p.m.f) of X is given below :
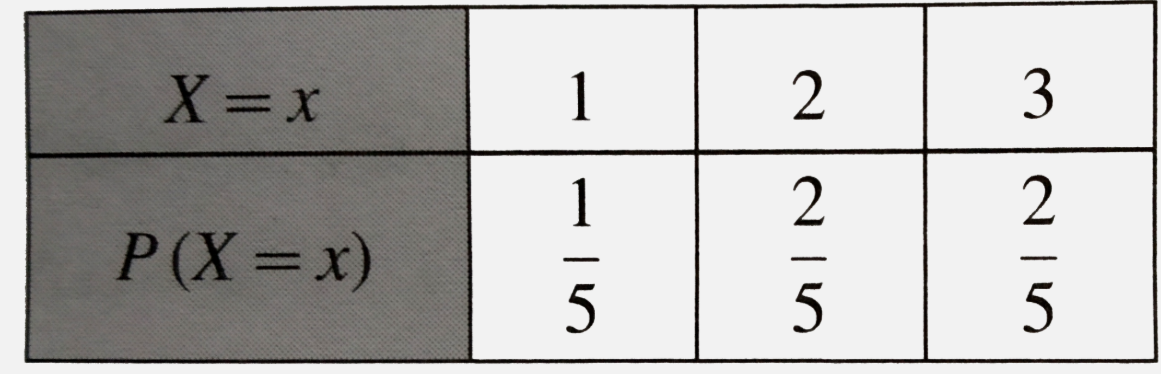
Find E(X2)
View SolutionThe probability mass function (p. m. f.) of X is given below :
∣∣∣X=x123P(X=x)152525∣∣∣ find E(X2)
View SolutionA probability distribution of a variable X is given below: X:01234 P(X):0.10.250.30.20.15 Find (i) Var(X) (ii) Var(X2)
View SolutionFor X~B (n,p), n = 10, E (X) = 5, then Var (X) =
View SolutionThe p.m.f. of a r.v. X is as follows :
P(X=0)=3k3,P(X=1)=4k−10k2,P(X=2)=5k−1,
P(X=x)=0 for any other values of x, then P(X<1)=
View Solution


