If Laspeyre’s and Paasche’s Price Index Numbers are 50 & 72 respectively, find Dorbish-Bowley’s and Fisher’s Price Index Numbers
The correct Answer is:61,60
To find Dorbish-Bowley's and Fisher's Price Index Numbers given Laspeyre’s and Paasche’s Price Index Numbers, we can follow these steps:
1. Identify the Given Values:
- Laspeyre’s Price Index Number (P01 of L) = 50
- Paasche’s Price Index Number (P01 of P) = 72
2. Calculate Dorbish-Bowley’s Price Index Number:
- The formula for Dorbish-Bowley’s Price Index Number (P01 of D) is:
P01ofD=P01ofL+P01ofP2
- Substitute the given values:
P01ofD=50+722
- Calculate:
P01ofD=1222=61
3. Calculate Fisher’s Price Index Number:
- The formula for Fisher’s Price Index Number (P01 of F) is:
P01ofF=√P01ofL×P01ofP
- Substitute the given values:
P01ofF=√50×72
- Calculate the product:
50×72=3600
- Now, take the square root:
P01ofF=√3600=60
Final Answers:
- Dorbish-Bowley’s Price Index Number = 61
- Fisher’s Price Index Number = 60
---
- Laspeyre’s Price Index Number (P01 of L) = 50
- Paasche’s Price Index Number (P01 of P) = 72
- The formula for Dorbish-Bowley’s Price Index Number (P01 of D) is:
P01ofD=P01ofL+P01ofP2
- Substitute the given values:
P01ofD=50+722
- Calculate:
P01ofD=1222=61
- The formula for Fisher’s Price Index Number (P01 of F) is:
P01ofF=√P01ofL×P01ofP
- Substitute the given values:
P01ofF=√50×72
- Calculate the product:
50×72=3600
- Now, take the square root:
P01ofF=√3600=60
- Dorbish-Bowley’s Price Index Number = 61
- Fisher’s Price Index Number = 60
Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II 5. INDEX NUMBERS (V Activity)
1 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II LINEAR PROGRAMMING PROBLEMS (1. Select the most appropriate option for each of the following. )
12 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II 5. INDEX NUMBERS (III) State whether each of the following is True or False.)
9 Videos
- PROBABILITY DISTRIBUTIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
9 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CHOICE QUESTIONS
8 Videos
Similar Questions
Knowledge Check
Fisher’s Price Index Number is
A√P01(L)×P01(P)BP01(L)×P01(P)C√P01(L)×P01(P)×100D√P01(L)×P01(P)We use price index numbers
ATo measure pricesBTo measure and compare prices,CTo measure quantityDNone of theseWalsh's Price Index Number is given by
A∑(q0√p0p1)∑(q1√p0p1)×100B∑(p0√q0q1)∑(p1√q0q1)×100C∑(q1√p0p1)∑(q0√p0p1)×100D∑(p1√q0q1)∑(p0√q0q1)×100
Define consumer price index number.
View SolutionFisher's Price Index Number is given by ..............
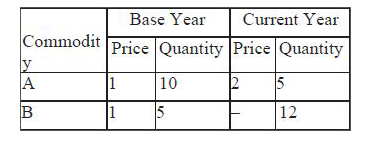
View SolutionFrom the following data, find Fisher's Ideal Index Number:
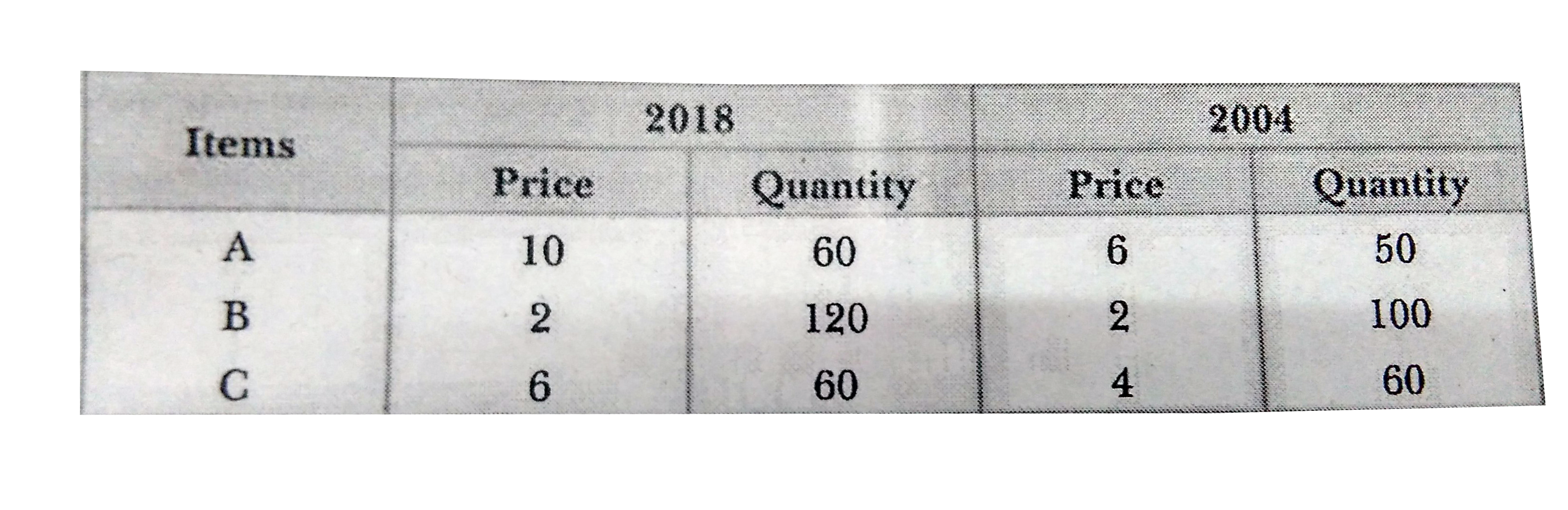
View SolutionCalculate a) Laspeyre’s, b) Paasche’s, and c) Dorbish- Bowley’s Price Index Numbers for following data.
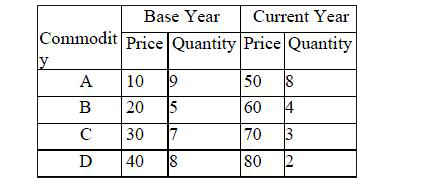
View SolutionDorbish Bowley’s Price Index Number is
View Solution