Four identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
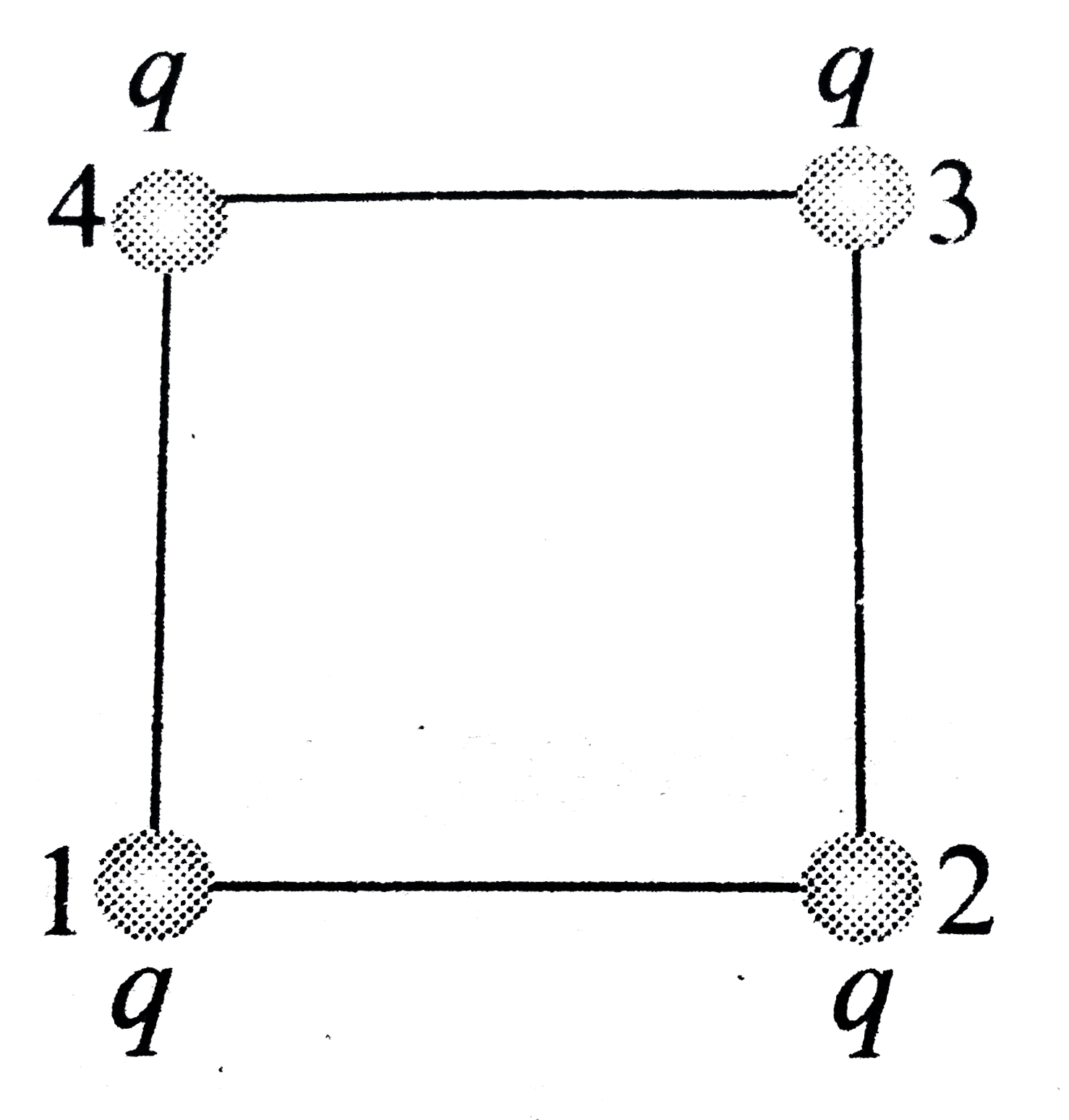 .
.
Method 1 (using direct formula) : U=U12+U13+U14+U23+U24+U34
Kq2a+Kq2a√2+Kq2a+Kq2a+Kq2a√2+Kq2a=[4Kq2a+2Kq2a√2]=2Kq2a[2+1√2]
Method 2 [Using, U=12(U1+U2+....)] :
U1= total P.E. of charge at corner 1 due to all other charges.
U2= total P.E. of charge at corner 2 due to all other charges.
U3=total P.E. of charge at corner 3 due to all other charges.
U4= total P.E. of charge at corner 4 due to all other charges.
since, due to symmetery, U1=U2=U3=U4
UNet=U1+U2+U3+U42=2U1=2[Kq2a+Kq2a+Kq2√2a]=2Kq2a[2+1√2]
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Problems
22 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
Four identical charges q are placed at the corners of a square of side a. Find the potential energy of one of the charges due to the remaining charges.
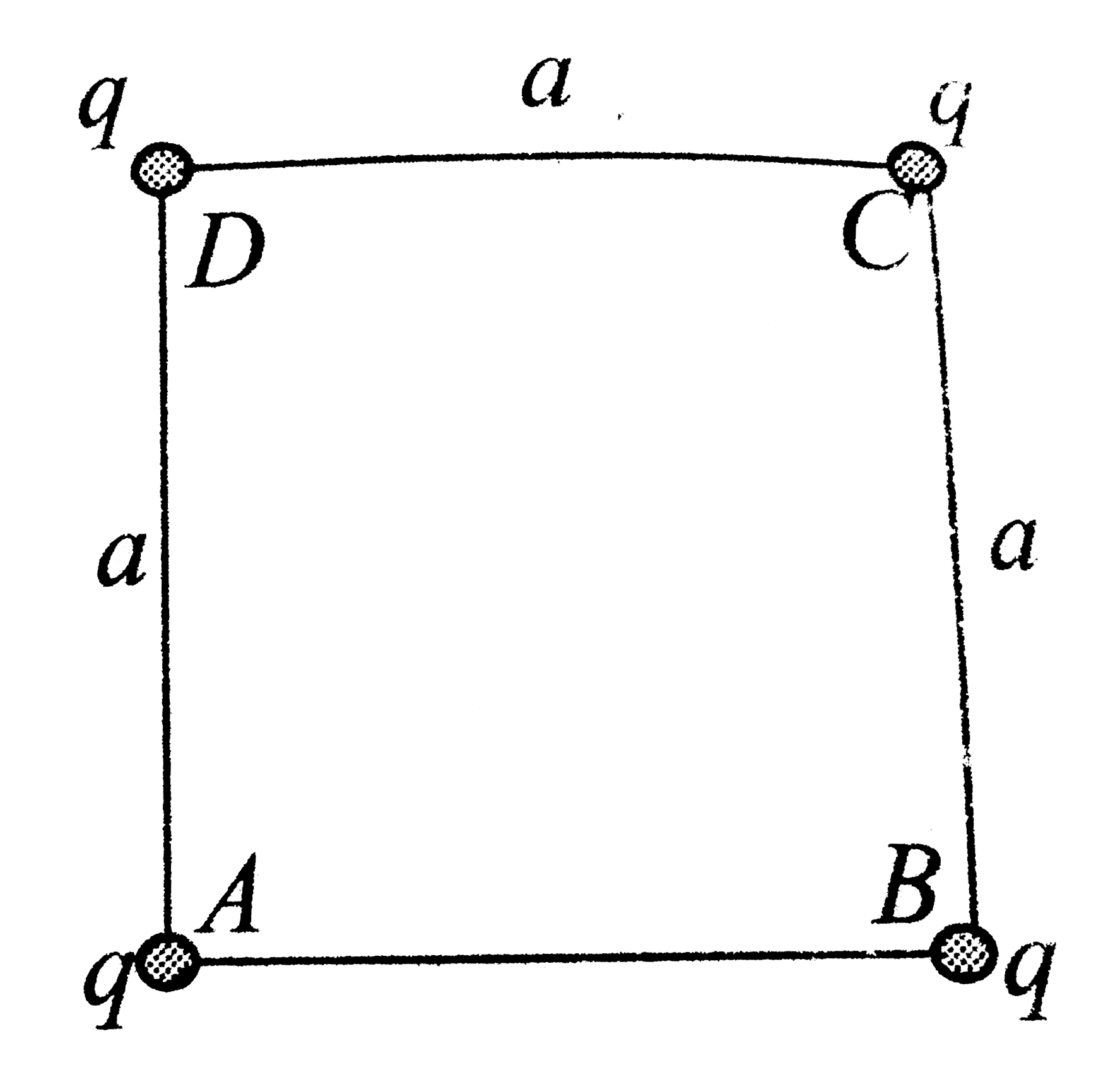 .
.
View SolutionSix equal point charges q each are placed at six corners of a hexago of side a. Find out potential energy of charge system
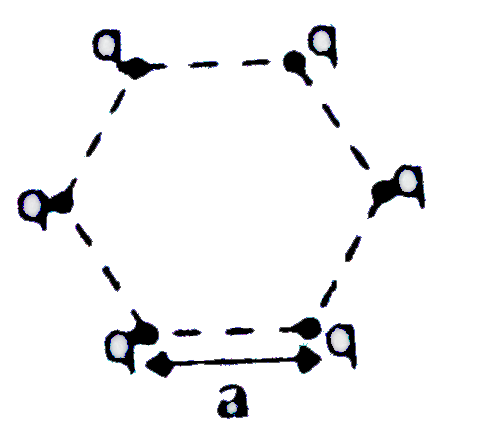
View SolutionFour identical charges each .q. are placed at four corners of a square of side .a.. Find the charge to be placed at the centre of the square so that the system of charges is in equilibrium
View SolutionFour small point charges (each of equal magnitude q) are placed at four corners of a regular tetrahedron of side a. find out potential energy of charge system
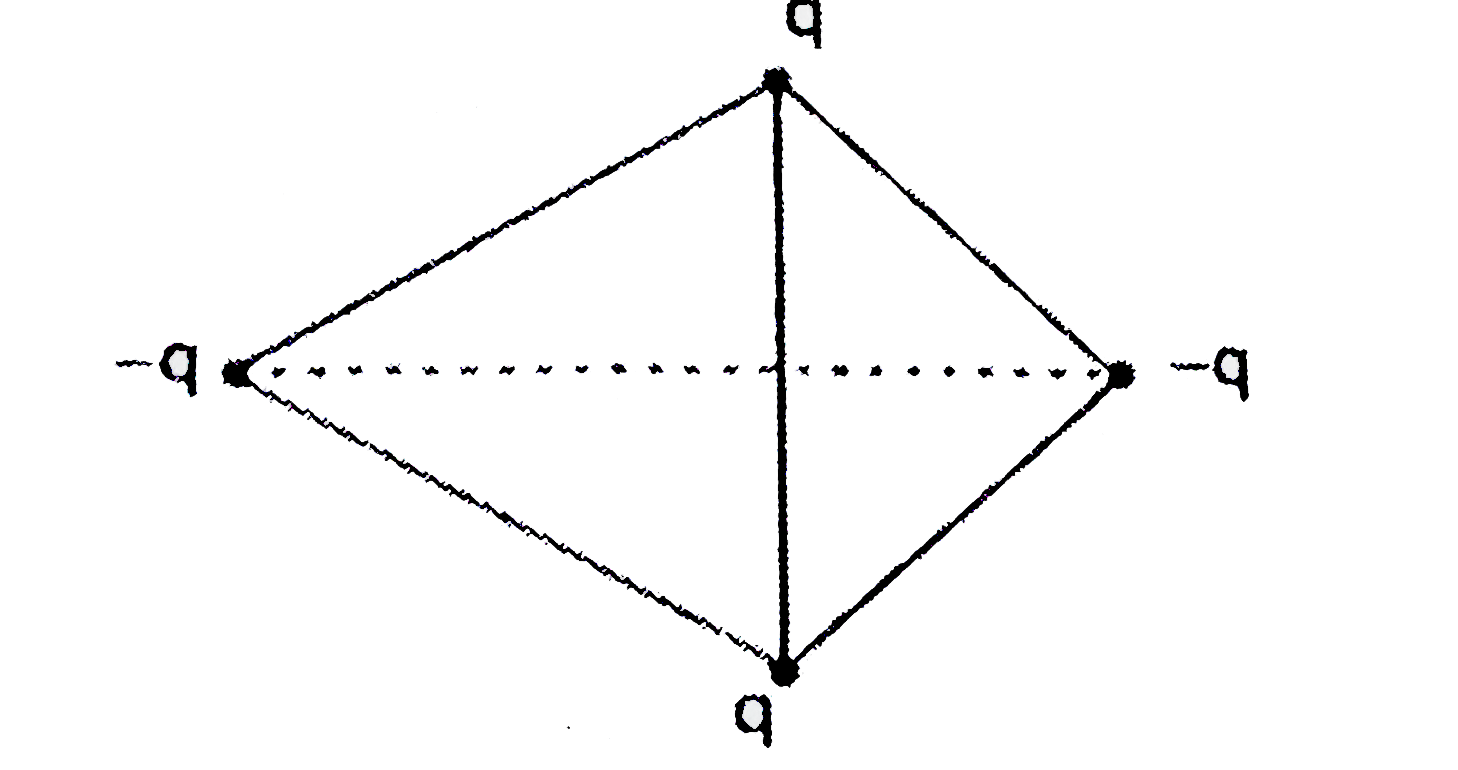
View SolutionFour point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.
View SolutionA point charge Q is placed at the corner of a square of side a. Find the flux through the square.
View SolutionA charge Q is placed at each corner of a cube of side a. The potential at the centre of the cube is
View SolutionFour identical positive point charges Q are fixed at the four corners of a square of side length l. Another charged particle of mass m and charge +q is projected towards centre of square from a large distance along the line perpendicular to plane of square. The minimum value of initial velocity v0 (in m/s) required to cross the square is ?
(m=1gm,l=4√2m,Q=1μc,q=0.5μc)

View SolutionIf identical charges (−q) are placed at each corner of a cube of side b, then electric potential energy of charge (+q) which is placed at centre of the cube will be
View SolutionFour identical point charges are placed at the corners of a square, A fifth point charge placed at the center of the square experiences zero net force . Is this a stable equilirium for the fifth charge? Explain.
View Solution
