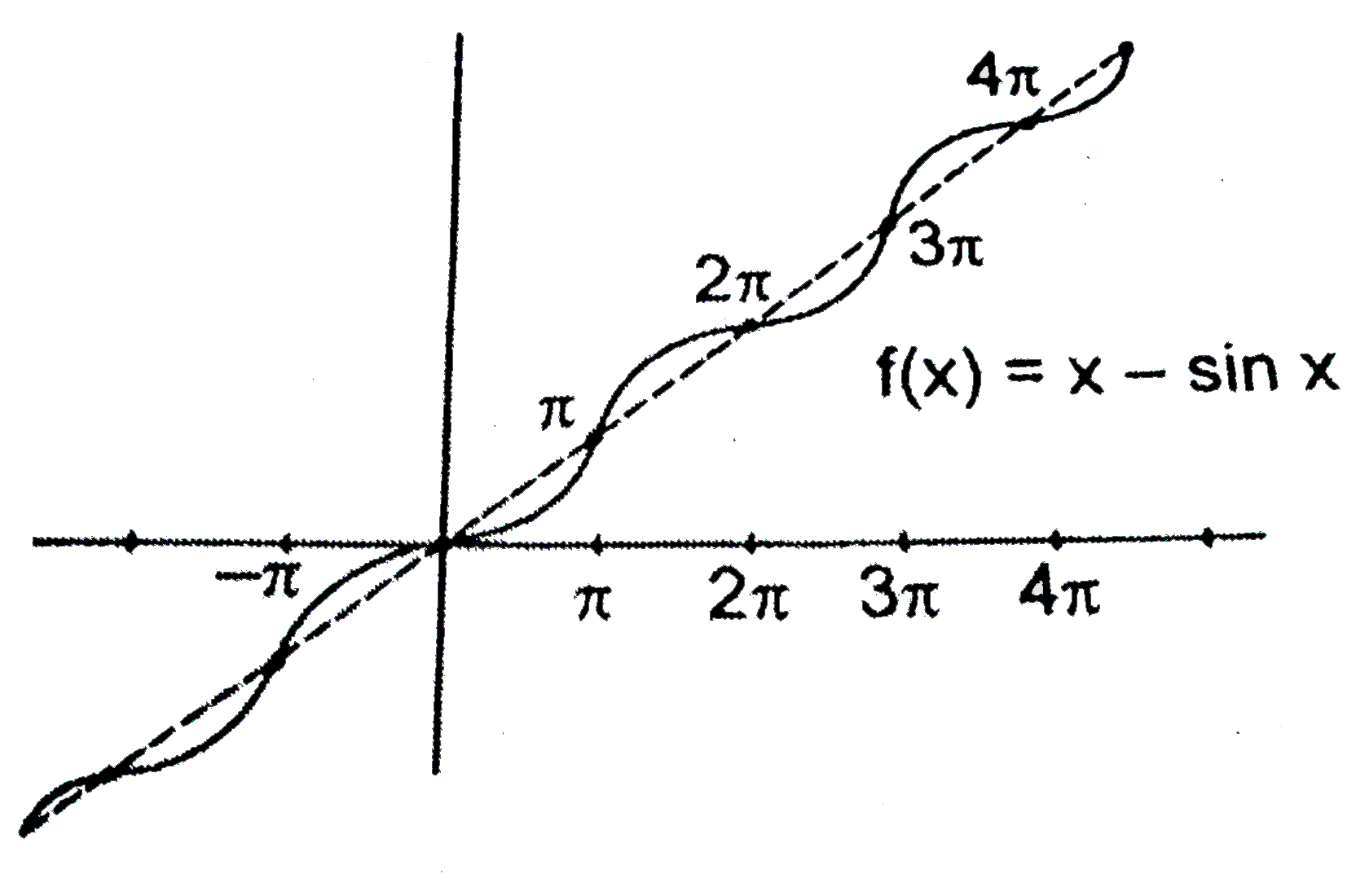
Let f(x)=x- sinx. Find the intervals of monotonicity.
f'(x)=1−cosx
Now f'(x) >0 every where except at x=0,±2π±4π etc. But all these points are discrete (countble) and do not form an interval. Hence we can conclude that f(x) is stricitly increasing in R. In fact we can also see it graphically.
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Self Practice Problems
36 Videos
- APPLICATION OF DERIVATIVESBOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise -1A
5 Videos
- COMBINATORICSBOOK - RESONANCE ENGLISHCHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)
5 Videos
Similar Questions
Let f (x)=x3. Find the intervals of monotonicity.
View SolutionFind the intervals of monotonicity of the function y=2x2−log|x|,x≠0
View SolutionLet g(x)=f(x)+f(1−x) and f''(x)>0∀x∈(0,1). Find the intervals of increase and decrease of g(x).
View SolutionLet f:[−π/2,π/2]→[−1,1] where f(x)=sinx. Find whether f(x) is one-one or not.
View SolutionLet f(x) =x - tan−1x. Prove that f(x) is monotonically increasing for x∈R
View SolutionLet f(x)=(x−3)(x+2)(x+5)(x+1)(x−7). Find the intervals were f(x) is positive or negative .
View SolutionLet f(x) =x3−3x+2. Examine the monotonicity of function at points x=0.1,2
View Solutionf(x)=sinx+cosx+3. find the range of f(x).
View SolutionLet f(x)=2x2x2+5x+2, find the interval for which f(x)>0.
View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x) = sinx + cos x in the interval [0,π/2].
View Solution
