Given that:
ΔG∘F(CuO)=−30.4Kcal/mole
ΔG∘f(Cu2O)=−34.98Kcal/mole T=298K
Now on the basis of above data which of the following predications will be most appropriate under the standard conditons and reversible reaction.
Finely divided form fof CuO Kept in excess O2 would be completely converted to Cu2O
Finely divided form of Cu2O kept in excess O2 would be Completely converted to CuO
Finely divided form of CuO kept in excess O2 would be converted to a mixture of CuO and Cu2O (having more of CuO)
Finely divided form of CuO kept in excess O2 would be converted to a mixture of CuO and Cu2O (having more of Cu2O)
The correct Answer is:B
To solve the problem, we need to analyze the given Gibbs free energy values for the reactions involving CuO and Cu2O. We will calculate the Gibbs free energy change for the reaction and then determine the equilibrium constant (K) to make predictions about the reaction's favorability.
1. Identify the Reaction:
The reaction we are considering is:
Cu2O (s)+O2(g)→2CuO (s)
2. Write the Gibbs Free Energy Change Equation:
The Gibbs free energy change (ΔG∘) for the reaction can be calculated using the standard Gibbs free energies of formation (ΔG∘f):
ΔG∘=ΔG∘f(products)−ΔG∘f(reactants)
3. Substitute the Given Values:
From the problem, we have:
- ΔG∘f(CuO)=−30.4kcal/mol
- ΔG∘f(Cu2O)=−34.98kcal/mol
Therefore, substituting these values into the equation:
ΔG∘=(2×(−30.4))−(−34.98)
ΔG∘=−60.8+34.98=−25.82kcal/mol
4. Convert to Joules:
To convert kcal to Joules (1 kcal = 4184 J):
ΔG∘=−25.82kcal/mol×4184J/kcal=−107,000J/mol≈−1.07×105J/mol
5. Calculate the Equilibrium Constant (K):
Using the relationship between Gibbs free energy and the equilibrium constant:
ΔG∘=−RTlnK
Rearranging gives:
K=e−ΔG∘/RT
Where R=8.314J/(mol K) and T=298K:
K=e1.07×105/(8.314×298)
K=e42.6≈1019
6. Conclusion:
Since K is a very large number (approximately 1019), this indicates that the reaction favors the formation of products (2 CuO) almost completely from Cu2O and O2 under standard conditions.
Final Answer:
The most appropriate prediction under standard conditions and reversible reaction is that Cu2O will almost completely convert to 2CuO.
The reaction we are considering is:
Cu2O (s)+O2(g)→2CuO (s)
The Gibbs free energy change (ΔG∘) for the reaction can be calculated using the standard Gibbs free energies of formation (ΔG∘f):
ΔG∘=ΔG∘f(products)−ΔG∘f(reactants)
From the problem, we have:
- ΔG∘f(CuO)=−30.4kcal/mol
- ΔG∘f(Cu2O)=−34.98kcal/mol
ΔG∘=(2×(−30.4))−(−34.98)
ΔG∘=−60.8+34.98=−25.82kcal/mol
To convert kcal to Joules (1 kcal = 4184 J):
ΔG∘=−25.82kcal/mol×4184J/kcal=−107,000J/mol≈−1.07×105J/mol
Using the relationship between Gibbs free energy and the equilibrium constant:
ΔG∘=−RTlnK
Rearranging gives:
K=e−ΔG∘/RT
Where R=8.314J/(mol K) and T=298K:
K=e1.07×105/(8.314×298)
K=e42.6≈1019
Since K is a very large number (approximately 1019), this indicates that the reaction favors the formation of products (2 CuO) almost completely from Cu2O and O2 under standard conditions.
The most appropriate prediction under standard conditions and reversible reaction is that Cu2O will almost completely convert to 2CuO.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - exercise-3 part-2 Advanced level Solutions
27 Videos
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - exercise-3 part-III Advanced level Solutions (STAGE-I)
6 Videos
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - exercise-3 Part:(I)
23 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - CHEMISTRY
50 Videos
Similar Questions
For the reaction: N2O4(g)⇔2NO2(g)
(i) In a mixture of 5molNO2 and 5 mol N2O4 and pressure of 20 bar. Calculate the value of ΔG for the reaction. Given ΔG∘f(NO2)=50 KJ/mol, ΔG∘f((N2O4)=100 KJ/mol and T=298 K. (ii) Predict the direction in which the reaction will shift, in order to attain equilibrium
[Given at T=298K,2.303RT=5.7KJ/mol.]
View SolutionFor the reaction: N2O4(g)⇔2NO2(g)
(i) In a mixture of 5molNO2 and 5 mol N2O4 and pressure of 20 bar. Calculate the value of ΔG for the reaction. Given ΔG∘f(NO2)=50 KJ/mol, ΔG∘f((N2O4)=100 KJ/mol and T=298 K. (ii) Predict the direction in which the reaction will shift, in order to attain equilibrium
[Given at T=298K,2.303RT=5.7KJ/mol.]
View SolutionThe heat of formation of C2H5OH(l) is −66kcal/mole. The heat of combustion of CH3OCH3(g) is -348 kcal/mole. ΔHf for H2O and CO2 are -68 kcal/mole respectively. Then, the ΔH for the isomerisation reaction C2H5OH(l)→CH3OCH3(g),and ΔE for the same are at T=25∘C
View SolutionStandard Gibb's energy of reaction (ΔrG∘) at a certain temperature can be computed ΔrG∘=ΔrH∘−T.ΔrS∘ and the change in the value of ΔrH∘ and ΔrS∘ for a reaction with temperature can be computed as follows :
ΔrH∘T2−ΔrH∘T1=ΔrC∘p(T2−T1)
ΔrS∘T2−ΔrS∘T1=ΔrC∘pln.(T2T1)
ΔrG∘=ΔrH∘−T.ΔrS∘
and by ΔrG∘=−RT lnKeq.
Consider the following reaction : CO(g)+2H2(g)⇔CH3OH(g)
Given : ΔfH∘(CH3OH,g)=−201 kJ/mol, ΔfH∘(CO,g)=−114 kJ/mol
S∘(CH3OH,g)=240 J/K-mol, S∘(H2,g)=29 JK−1 mol−1
S∘(CO,g)=198 J/mol-K, C∘p,m(H2)=28.8 J/mol-K
C∘p,m(CO)=29.4 J/mol-K, C∘p,m(CH3OH)=44 J/mol-K
and ln(320300)=0.06, all data at 300 K
ΔrS∘ at 300 K for the reaction is :
View SolutionStandard Gibb's energy of reaction (ΔrG∘) at a certain temperature can be computed ΔrG∘=ΔrH∘−T.ΔrS∘ and the change in the value of ΔrH∘ and ΔrS∘ for a reaction with temperature can be computed as follows :
ΔrH∘T2−ΔrH∘T1=ΔrC∘p(T2−T1)
ΔrS∘T2−ΔrS∘T1=ΔrC∘pln.(T2T1)
ΔrG∘=ΔrH∘−T.ΔrS∘
and by ΔrG∘=−RT lnKeq.
Consider the following reaction : CO(g)+2H2(g)⇔CH3OH(g)
Given : ΔfH∘(CH3OH,g)=−201 kJ/mol, ΔfH∘(CO,g)=−114 kJ/mol
S∘(CH3OH,g)=240 J/K-mol, S∘(H2,g)=29 JK−1 mol−1
S∘(CO,g)=198 J/mol-K, C∘p,m(H2)=28.8 J/mol-K
C∘p,m(CO)=29.4 J/mol-K, C∘p,m(CH3OH)=44 J/mol-K
and ln(320300)=0.06, all data at 300 K
ΔrH∘ at 300 K for the reaction is :
View SolutionStandard Gibb's energy of reaction (ΔrG∘) at a certain temperature can be computed ΔrG∘=ΔrH∘−T.ΔrS∘ and the change in the value of ΔrH∘ and ΔrS∘ for a reaction with temperature can be computed as follows :
ΔrH∘T2−ΔrH∘T1=ΔrC∘p(T2−T1)
ΔrS∘T2−ΔrS∘T1=ΔrC∘pln.(T2T1)
ΔrG∘=ΔrH∘−T.ΔrS∘
and by ΔrG∘=−RT lnKeq.
Consider the following reaction : CO(g)+2H2(g)⇔CH3OH(g)
Given : ΔfH∘(CH3OH,g)=−201 kJ/mol, ΔfH∘(CO,g)=−114 kJ/mol
S∘(CH3OH,g)=240 J/K-mol, S∘(H2,g)=29 JK−1 mol−1
S∘(CO,g)=198 J/mol-K, C∘p,m(H2)=28.8 J/mol-K
C∘p,m(CO)=29.4 J/mol-K, C∘p,m(CH3OH)=44 J/mol-K
and ln(320300)=0.06, all data at 300 K
ΔrS∘ at 320 K is :
View SolutionStandard Gibb's energy of reaction (ΔrG∘) at a certain temperature can be computed ΔrG∘=ΔrH∘−T.ΔrS∘ and the change in the value of ΔrH∘ and ΔrS∘ for a reaction with temperature can be computed as follows :
ΔrH∘T2−ΔrH∘T1=ΔrC∘p(T2−T1)
ΔrS∘T2−ΔrS∘T1=ΔrC∘pln.(T2T1)
ΔrG∘=ΔrH∘−T.ΔrS∘
and by ΔrG∘=−RT lnKeq.
Consider the following reaction : CO(g)+2H2(g)⇔CH3OH(g)
Given : ΔfH∘(CH3OH,g)=−201 kJ/mol, ΔfH∘(CO,g)=−114 kJ/mol
S∘(CH3OH,g)=240 J/K-mol, S∘(H2,g)=29 JK−1 mol−1
S∘(CO,g)=198 J/mol-K, C∘p,m(H2)=28.8 J/mol-K
C∘p,m(CO)=29.4 J/mol-K, C∘p,m(CH3OH)=44 J/mol-K
and ln(320300)=0.06, all data at 300 K
ΔrH∘ at 320 K is :
View SolutionA reaction is spontaneous if free energy change ΔG , for the reaction is negative . The question arises, how we can explain , the spontaneous of reversible reaction taking the example of dissociation equilibrium N2O4⇔2NO2(g) the variation of free energy with the fraction of N2O4 dissociated under standard conditions is shown in the figure below.
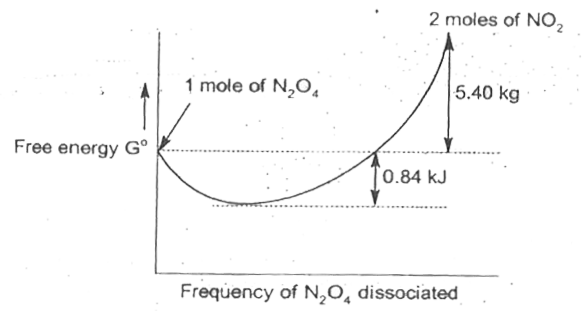
When 2 moles of NO2 change into equilibrium mixture the value of ΔG∘ is
View SolutionA reaction is spontaneous if free energy change ΔG for the reaction is negative . The question arises, how we can explain , the spontaneous reversible reaction. Taking the example of dissociation equilibrium N2O4⇔2NO2(g) the variation of free energy with the fraction of N2O4 dissociated under standard conditions is shown in the figure below.
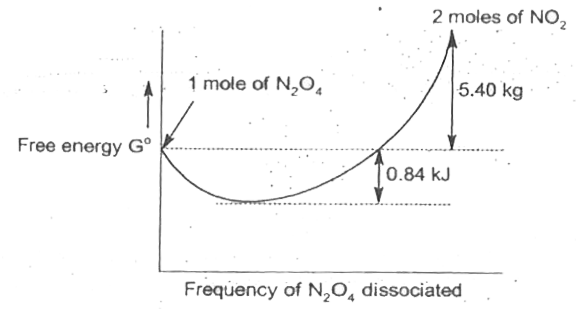
When 1 mole of N2O4 changes into the equilibrium mixture the value of ΔG∘ is
View SolutionΔfHΘ per mole of NH3(g).NO(g), and H2O(l) are −11.04+21.60 and −68.32kcal, respectively. Calculate the standard heat of reaction at constant pressure and at a constant volume for the reaction:
4NH3(g)+5O2(g)→4NO(g)+6H2O(l)
View Solution
