x1=5sin(ωt+30∘)
x2=10cos(ωt)
Find amplitude of resultant SHM.
x1=5sin(ωt+30∘)
x2=10sin(ωt+π2)
A=√52+102+2×5×10cos60∘
=√25+100+50=√175=5√7
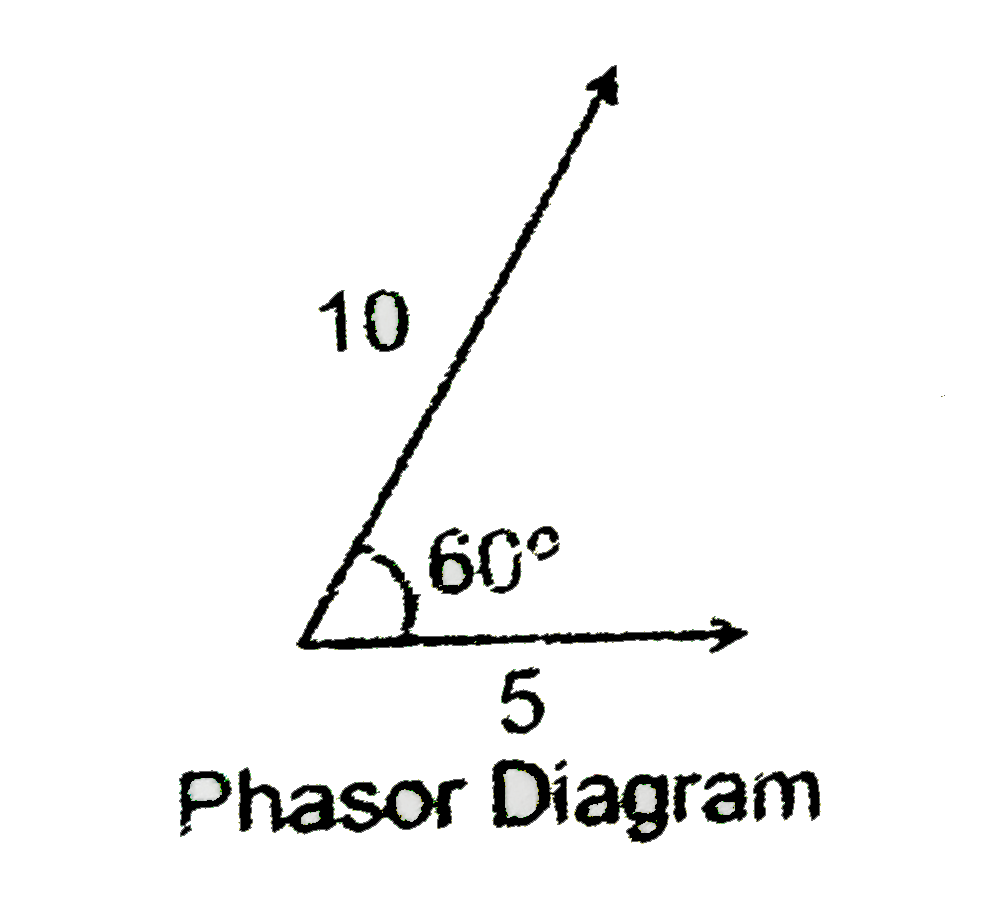
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Solved Miscellaneous Problems
9 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Board Level Exercise
24 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
x1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
Find amplitude of resultant SHM.
View Solutionx1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
Find amplitude of resultant SHM.
View Solutionx1=3sinωt , x2=4cosωt. Find (i) amplitude of resultant SHM, (ii) equation of the resultant SHM.
View Solutionx1=3sinωt⇒x2=4cosωt. Find (i) amplitude of resultant SHm, (ii) equation of the resultant SHm.
View Solutionx1=3sinωt,x2=4cosωt
Find (i) amplitude of resultant SHM, (ii) equation of the resultant SHM.
View SolutionA particle is subjected to SHM as given by equations x1=A1sinωt and x2=A2sin(ωt+π/3).The maximum acceleration and amplitude of the resultant motion are it amax and A,respectively , then
View SolutionTwo waves are given as y1=3Acos(ωt−kx) and y2=Acos(3ωt−3kx) . Amplitude of resultant wave will be ____
View SolutionThe displacement of two identical particles executing SHM are represented by equations x1=4sin(10t+π6)&x2=5cos(ωt) For what value of ∙, energy of both the particles is same.
View SolutionIf a waveform has the equation y1=A1sin(ωt−kx) & y2=A2cos(ωt−kx) , find the equation of the resulting wave on superposition.
View SolutionA particle is subjected to two simple harmonic motions, one along the X-axis and the other on a line making an angle of 45∘ with the X-axis. The two motions are given by
x=x0sinωt and s=s0sinωt.
find the amplitude of the resultant motion.
View Solution
