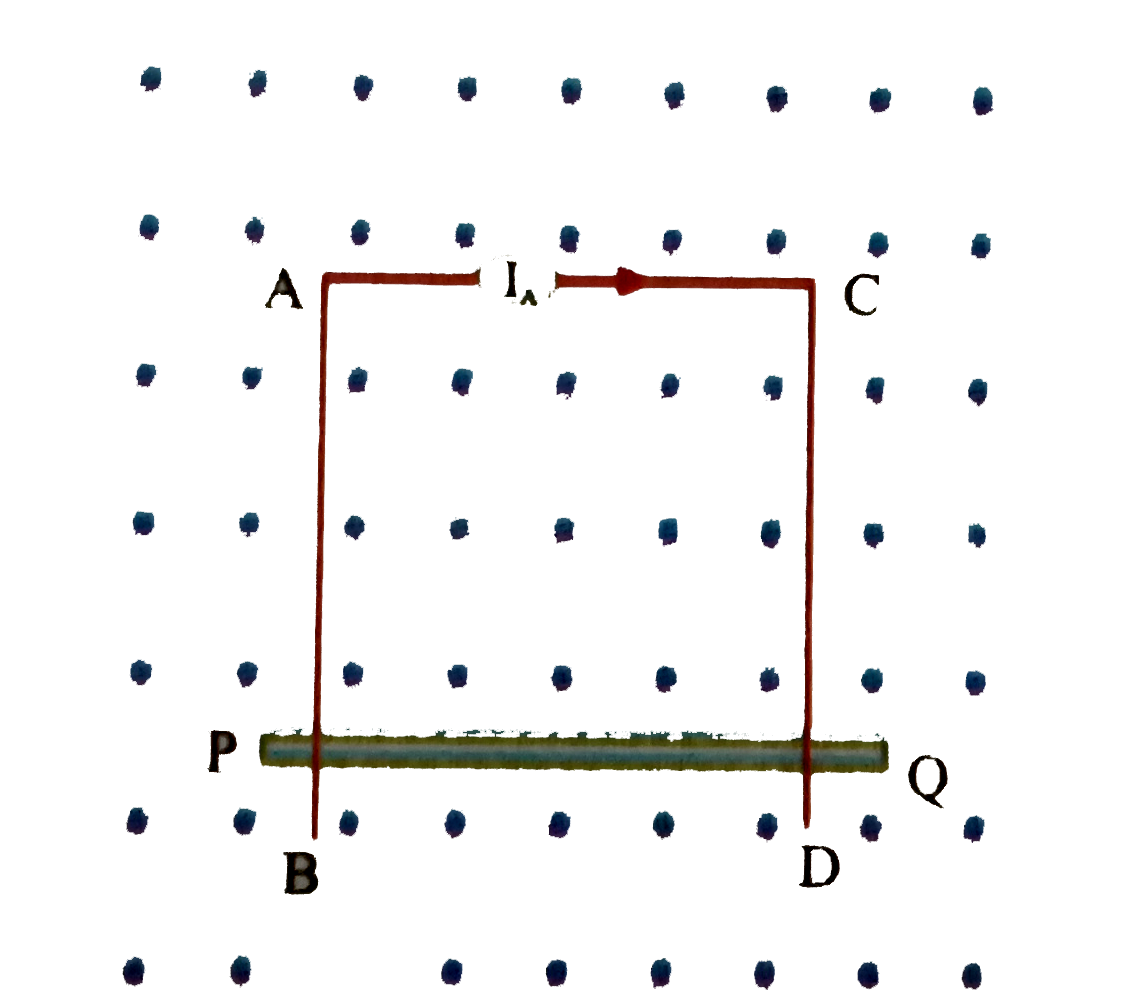
AB and CD are fixed conducting smooth rails plaed in a vertical plane and joined by a constant current source at tits upper end PQ is a conducting rod which is freee to slide on the rails. A horizontal uniform magnetic field exiets in space as shown. If the rod PQ is released from rest then,

The rod PQ may move downward with constant acceleration
The rod PQ may move upward with constant acceleration
The rod will move downward with decreasing acceleration and finally acquire a constant speed
either A and B
The correct Answer is:D
It the magnitude of lA is very large such that force due to magnetic field on PQ exceeds its weight then it will move upwards otherwise it will move downwards.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 1
14 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 2
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1
63 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
Similar Questions
AB and CD are fixed conducting smooth rails placed in a vertical plane and joined by a constant current source at its upper end. PQ is a conducting rod which is free to slide on the rails. A horizontal uniform magnetic field exists in space as shown in figure. If the rod PQ is released from rest then,
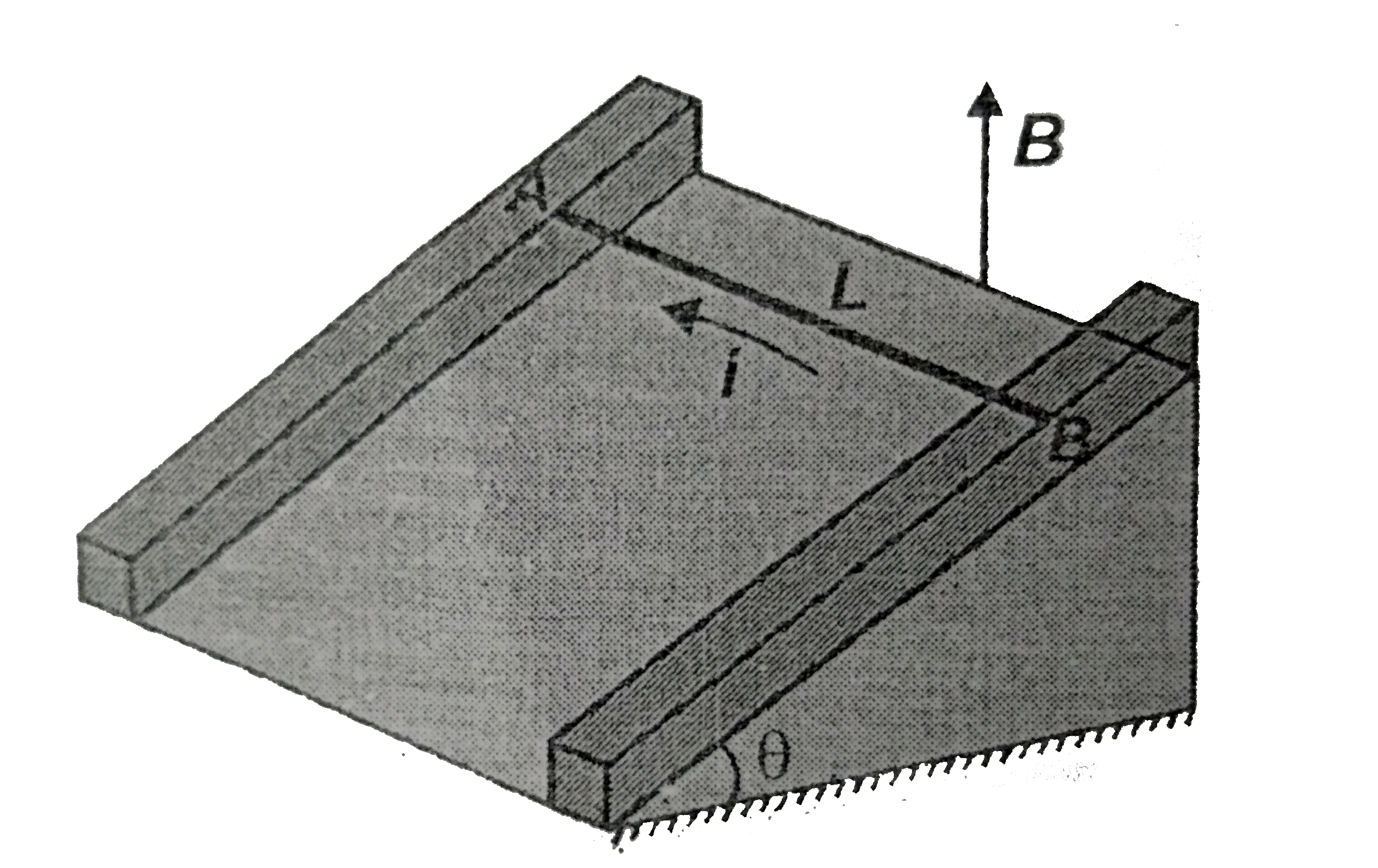
View SolutionOn an inclined plane, two conducting rails are fixed along the line of greatest slope. A conducting rod AB is placed on the radils so that it is horizontal. A vertically upward uniform magnetic field is present in the region. A current i flows through AB from B to A. The mass of AB is m and the coefficient of friction between the rod and rails is μ. Find the minimum and maximum value of B, so that the rod can stay in equilibrium. Assume that μ<tanθ
View SolutionTwo long parallel horizontal rails a, a distance d aprt and each having a risistance λ per unit length are joing at one end by a resistance R. A perfectly conduction rod MN of mass m is free to slide along the rails without friction (see figure). There is a uniform magnetic field of induction B normal to the plane of the paper and directed into the paper. A variable force F is applied to the rod MN such that, as the rod moves a constant current flows through R.
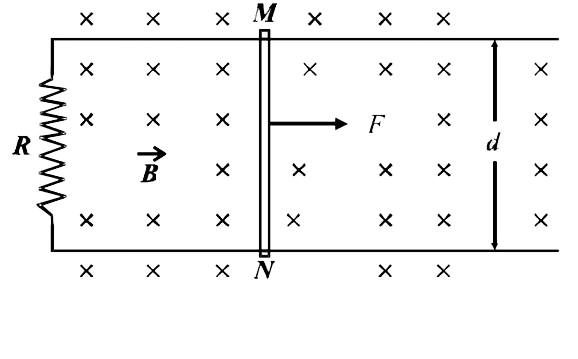
(i) Find the velocity of the rod and the applied force F as function of the distance x of the rod from R.
(ii) What fraction of the work done per second by F is converted into heat?
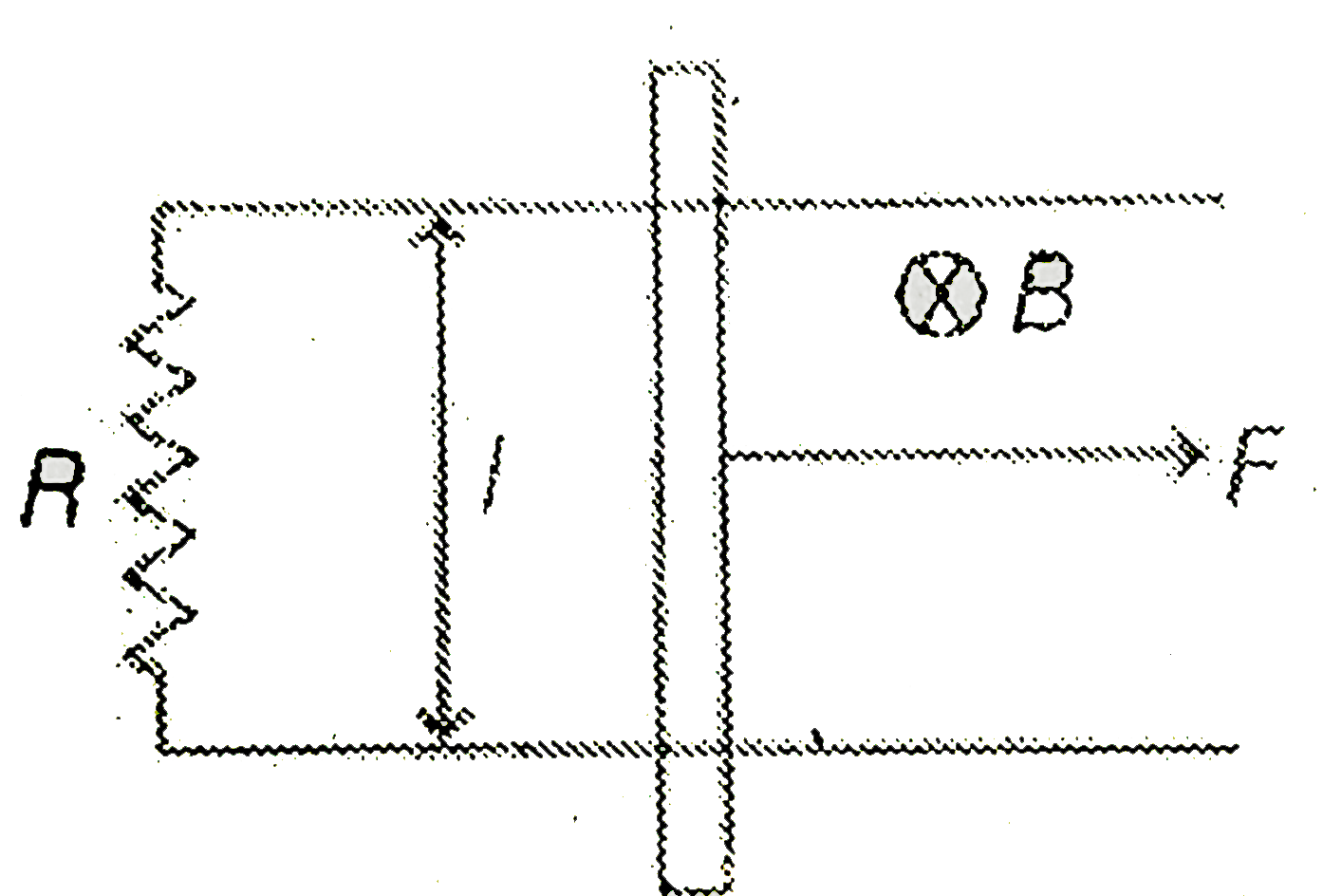
View SolutionA constant force is being applied on a road of length 'l' kept at rest on two parallel conducting rails connected at ends by resistance R in uniform magnitic field B shown.
View SolutionStatement I: A resistance R is connected between the two ends of the parallel smooth conducting rails. A conducting rod lies on these fixed horizontal rails and a uniform constant magnetic field B exists perpendicular to the plane of the rails as shown in Fig. if the rod is given a velocity υ and released as shown in Fig. 3.188, it will stop after some time. the total work done by magnetic field negative.

Statement II: If force acts opposite to direction of velocity its work done is negative.
View SolutionA vertical ring of radius r and resistance on R falls vertically. It is in contact with two vertical rails which are joined at the top. The rails are without friction and resistance. There is a horizontal uniform, magnetic field of magnitude B perpendicular to the plane of the ring and the rails. When the speed of the ring is v , the current in the section PQ is
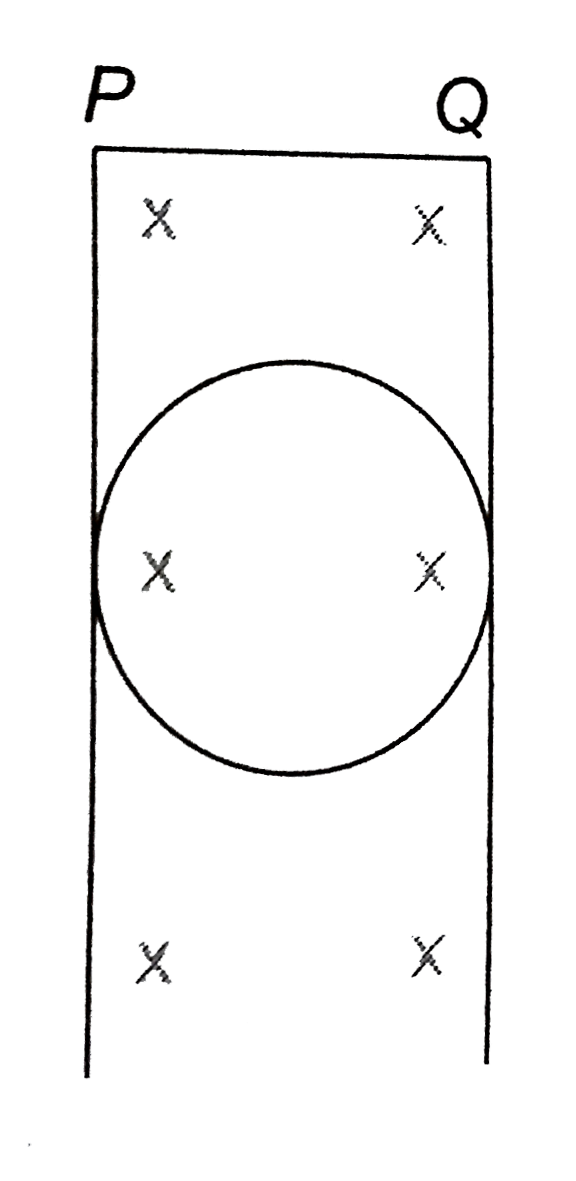
View SolutionA vertical ring of radius r and resistance on R falls vertically. It is in contact with two vertical rails which are joined at the top. The rails are without friction and resistance. There is a horizontal uniform, magnetic field of magnitude B perpendicular to the plane of the ring and the rails. When the speed of the ring is v , the current in the section PQ is

View SolutionA conductor bar with mass m and length L slides over horizontal rails that are connected to a voltage source. The voltage source maintains a constant current I in the rails and bar, and constant, uniform, vertical magnetic field →B fills the region between the rails (as shown in Fig.)
If the bar has mass m, find the distance d that the bar must move along the rails from rest to attain speed v.

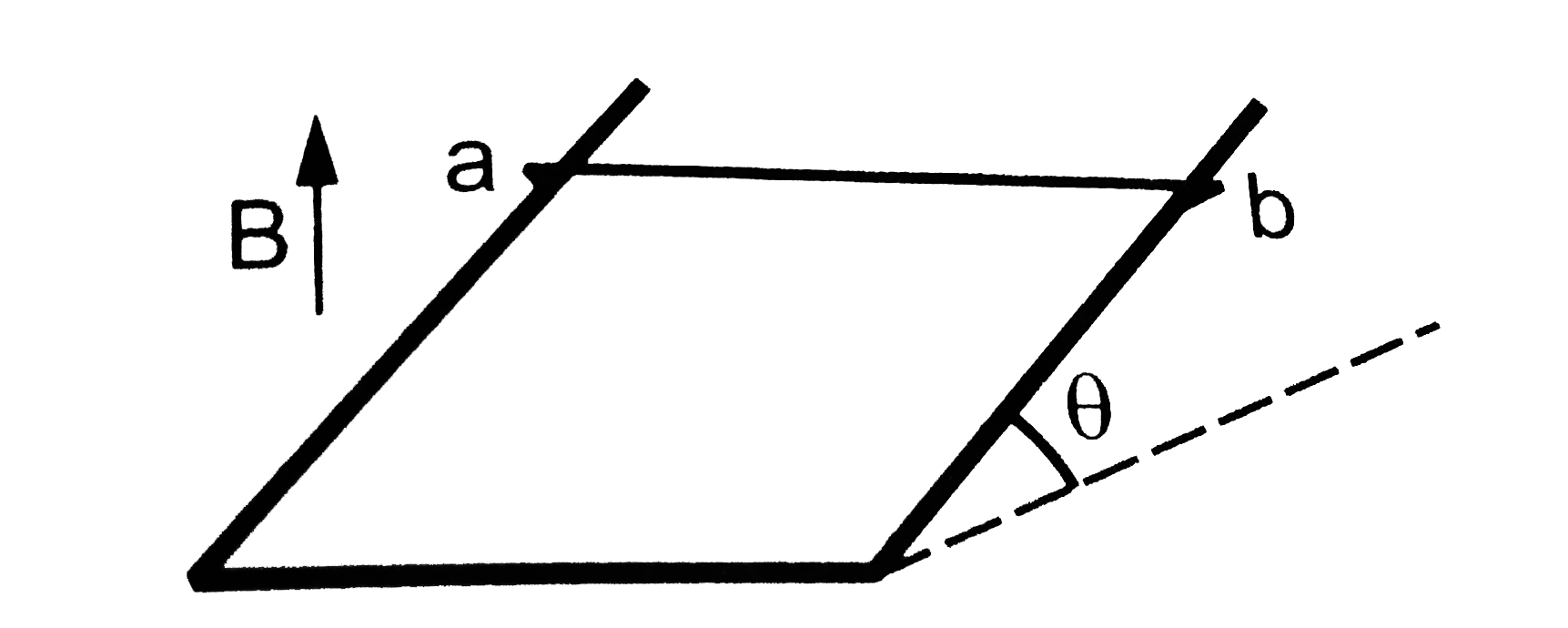
View SolutionA wire ab of length l, mass m and resistance R slided on a smooth, thick pair of metallic rails joined at the bottom as shown in . The plane of the the rails makes an angle θ with the horizontal. A vertical magnetic field B exists in the ragion. if the wire slides on the rails at a constant speed v, show that B=√mgRsinθvl2cosθ.
View SolutionIn the figure shown a uniform conducing rod of mass m and length l is suspended invertical plane by two conducing springs of spring constant k each. Upper end of springs are connected to each other by a capacitor of capacitance C. A uniform horizontal magnetic field (B0) perpendicular to plane of springs in space initially rod is in equillibrium. If the rod is pulled down and released, it performs SHM. (Assume resistance of springs and rod are negligible)

Find the period of oscillation of rod.
View Solution
