A uniform solid sphere of mass M and radius R is rotating with respect to its diameter, with a constant angular velocity ω in free space (i.e., there is no one to exert any force on sphere). Consider an hemispherical part of the sphere (such that axis of rotation lies in the place dividing the sphere in two hemisphere). Net force on this hemisphere due to another hemisphere is nMω2R16. Here n is an integer. Find n
The correct Answer is:3
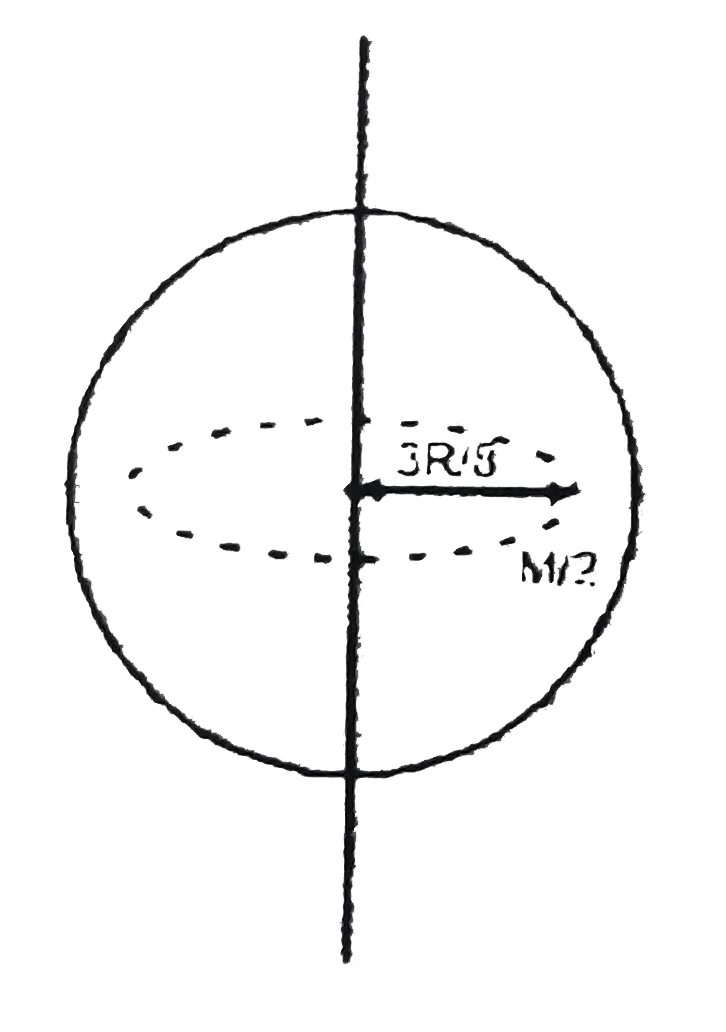
F=M2ω2(3R8)
F=3Mω2R16
Similar Questions
A solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View SolutionA ring and a solid sphere of same mass and radius are rotating with the same angular velocity about their diameteric axes then :-
View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View SolutionA ring of radius 'r' and mass per unit length 'm' rotates with an angular velocity 'ω' in free space then tension will be :
View SolutionA uniformly charged solid sphere a mass M, radius R having charge Q is rotated about its diameter with frequency f0. The magnetic moment of the sphere is
View SolutionA uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
View SolutionA solid sphere of mass 2 kg and radius 1 m is free to rotate about an axis passing through its centre. Find a constant tangential force F required to the sphere with ω = 10 rad/s in 2 s.
View SolutionSolid uniform conductiong sphere of mass 'm' and charge Q, rotates about its axis of symmetry with constant angular velocity 'ω' then the ratio of magnetic moment to the moment of inertia of the sphere is xQω6m then x is :(Neglect induced charges due to centrifugal force)
View SolutionFind the ratio of the total surface area of a sphere and a hemisphere of same radius.
View SolutionA solid sphere is rotating with a constant angular velocity about an axis touching the surface. Its angular momentum will be:
View Solution
