For an ideal solution, if a graph is plotted between 1PT and yA (mole fraction of A in vapour phase) where p0A>p0B then
intercept of the graph =1p0B
slope of the graph =(1p0A+1p0B)
slope of the graph (1p0B−1p0B)
the graph is linear
The correct Answer is:A, C, D
To solve the problem, we need to analyze the relationship between the total pressure PT and the mole fraction of component A in the vapor phase yA for an ideal solution. We will derive the equation and identify the characteristics of the graph plotted between 1PT and yA.
Step 1: Understand the relationship for an ideal solution
For an ideal solution, the total vapor pressure PT is given by Raoult's Law:
PT=P0A⋅xA+P0B⋅xB
where:
- P0A and P0B are the vapor pressures of pure components A and B, respectively.
- xA and xB are the mole fractions of components A and B in the liquid phase.
Step 2: Express xA in terms of yA
Since xA+xB=1, we can express xB as:
xB=1−xA
Now, substituting xB in the equation for PT:
PT=P0A⋅xA+P0B⋅(1−xA)=P0A⋅xA+P0B−P0B⋅xA
This simplifies to:
PT=(P0A−P0B)⋅xA+P0B
Step 3: Relate yA and PT
The mole fraction of A in the vapor phase yA is given by:
yA=PAPT
where PA=P0A⋅xA (from Raoult's Law).
Step 4: Substitute PA in terms of yA
From the expression for PT, we can express PA:
PA=P0A⋅xA
Substituting this into the equation for yA:
yA=P0A⋅xAPT
Step 5: Rearranging the equation
Now, we can express 1PT:
1PT=1P0A⋅xA+P0B⋅(1−xA)
This leads to the equation:
1PT=1P0B+1P0A−P0B⋅yA
This is a linear equation of the form y=mx+c, where:
- y=1PT
- x=yA
- The slope m=1P0A−P0B
- The intercept c=1P0B
Step 6: Analyze the graph
From the derived equation, we can conclude:
1. The intercept of the graph is 1P0B.
2. The slope of the graph is 1P0A−P0B.
3. The graph is linear.
Conclusion
Based on the analysis:
- The first option (intercept is 1P0B) is correct.
- The second option (slope is 1P0A+P0B) is incorrect.
- The third option (slope is 1P0A−P0B) is correct.
- The fourth option (the graph is linear) is correct.
Thus, the correct options are 1, 3, and 4.
For an ideal solution, the total vapor pressure PT is given by Raoult's Law:
PT=P0A⋅xA+P0B⋅xB
where:
- P0A and P0B are the vapor pressures of pure components A and B, respectively.
- xA and xB are the mole fractions of components A and B in the liquid phase.
Since xA+xB=1, we can express xB as:
xB=1−xA
Now, substituting xB in the equation for PT:
PT=P0A⋅xA+P0B⋅(1−xA)=P0A⋅xA+P0B−P0B⋅xA
This simplifies to:
PT=(P0A−P0B)⋅xA+P0B
The mole fraction of A in the vapor phase yA is given by:
yA=PAPT
where PA=P0A⋅xA (from Raoult's Law).
From the expression for PT, we can express PA:
PA=P0A⋅xA
Substituting this into the equation for yA:
yA=P0A⋅xAPT
Now, we can express 1PT:
1PT=1P0A⋅xA+P0B⋅(1−xA)
This leads to the equation:
1PT=1P0B+1P0A−P0B⋅yA
This is a linear equation of the form y=mx+c, where:
- y=1PT
- x=yA
- The slope m=1P0A−P0B
- The intercept c=1P0B
From the derived equation, we can conclude:
1. The intercept of the graph is 1P0B.
2. The slope of the graph is 1P0A−P0B.
3. The graph is linear.
Based on the analysis:
- The first option (intercept is 1P0B) is correct.
- The second option (slope is 1P0A+P0B) is incorrect.
- The third option (slope is 1P0A−P0B) is correct.
- The fourth option (the graph is linear) is correct.
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PT-01
Explore 30 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:Pt-02
Explore 30 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - III CHEMISTRY
Explore 20 Videos
- SURFACE CHEMISTRYBook:RESONANCE ENGLISHChapter:SURFACE CHEMISTRYExercise:Section - 5
Explore 1 Video
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:CHEMISTRY
Explore 50 Videos
Similar Questions
For a ideal liquid solution with P∘A>P∘B, which relation betweenXA ((mole fraction of A in liquid phase) and YA(mole fraction of A in vapour phase) is correct ?
View SolutionFor an ideal binary liquid solution with p∘A>p∘B, which is a relation between XA (mole fraction of A in liquid phase) and YA (mole fraction of A in vapour phase) is correct, XBandYB are mole fractions of B in liquid and vapour phase respectively?
View SolutionFor an ideal binary liquid solutions with P∘A>P∘B, which relation between χA (mole fraction of A in liquid phase) and YA (mole fraction of A in vapour phase) is correct :
View SolutionPA=(235y−125xy)mm of HgPA is partial pressure of A,x is mole fraction of B in liquid phase in the mixture of two liquids A and B and y is the mole fraction of A in vapour phase, then P∘B in mm of Hg is:
View SolutionXA and XB are the mole fraction of A and B respectively in liquid phase yA and yB are the mole fraction of A and B respective in vapour phase. Find out the slope of straight line if a graph is plotted 1yA along Y-axis against 1xA along X-axis gives straight line [p∘A and p∘B are vapour pressure of pure components A and B].
View SolutionIn the graph plotted between vapour pressure (V.P.) and temperature (T),
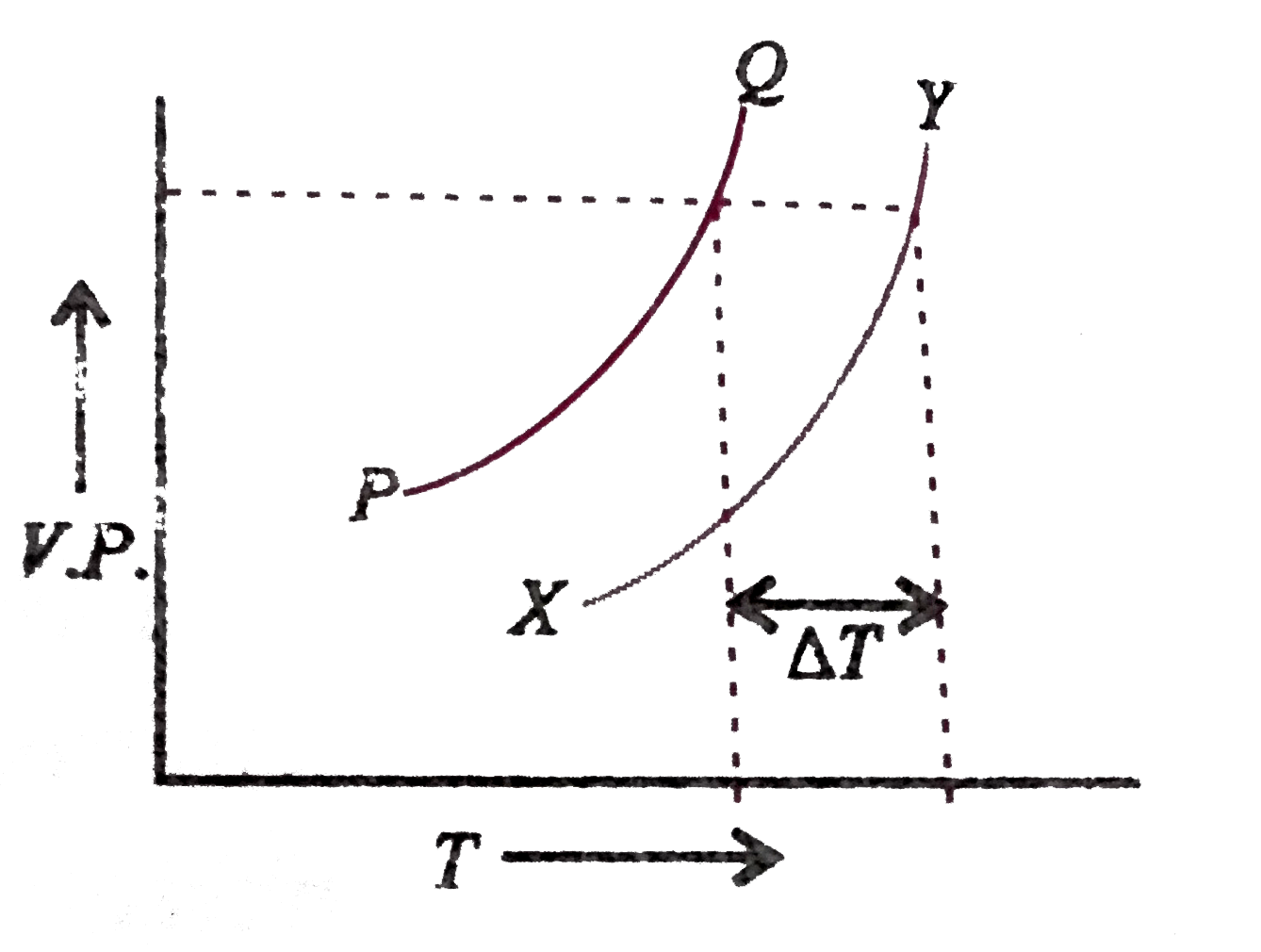
View SolutionMixture of volatile components A and B has total pressure ( in Torr ) p=265−130xA, where XA is mole fraction of A in mixture . Hence P∘A+P∘B= ( in T o r r).
View SolutionThe composition of vapour over a binary ideal solution is determined by the composition of the liquid. If xA and yA are the mole fractions of A in the liquid and vapour, respectively find the value of xA for which (yA−xA) has maximum. What is the value of the pressure at this composition?
View SolutionFor an binary mixture of A and B with p0A<p0B:
xA= mole fraction of A in solution
xB= mole fraction of B in solution
yA= mole fraction of A in vapour phase
yB= mole fraction of B in vapour phase solution
View SolutionTwo liquid A and B have vapour pressure in the ratio P∘A:P∘B=1.3 at a certain temperature.Assume A and B from an ideal solution and the ratio of mole fractions of A to B in the vapour phase is 4 : 3, then the mole fraction of B in the solution at the same tempreature is :
(a)15
(b)23
(c)45
(d)14
View Solution

