Graph show three waves that are separately send along a string that is stretched under a certain tension along x−axis. If ω1.ω2 and ω3 are their angular frequencies respectively then :
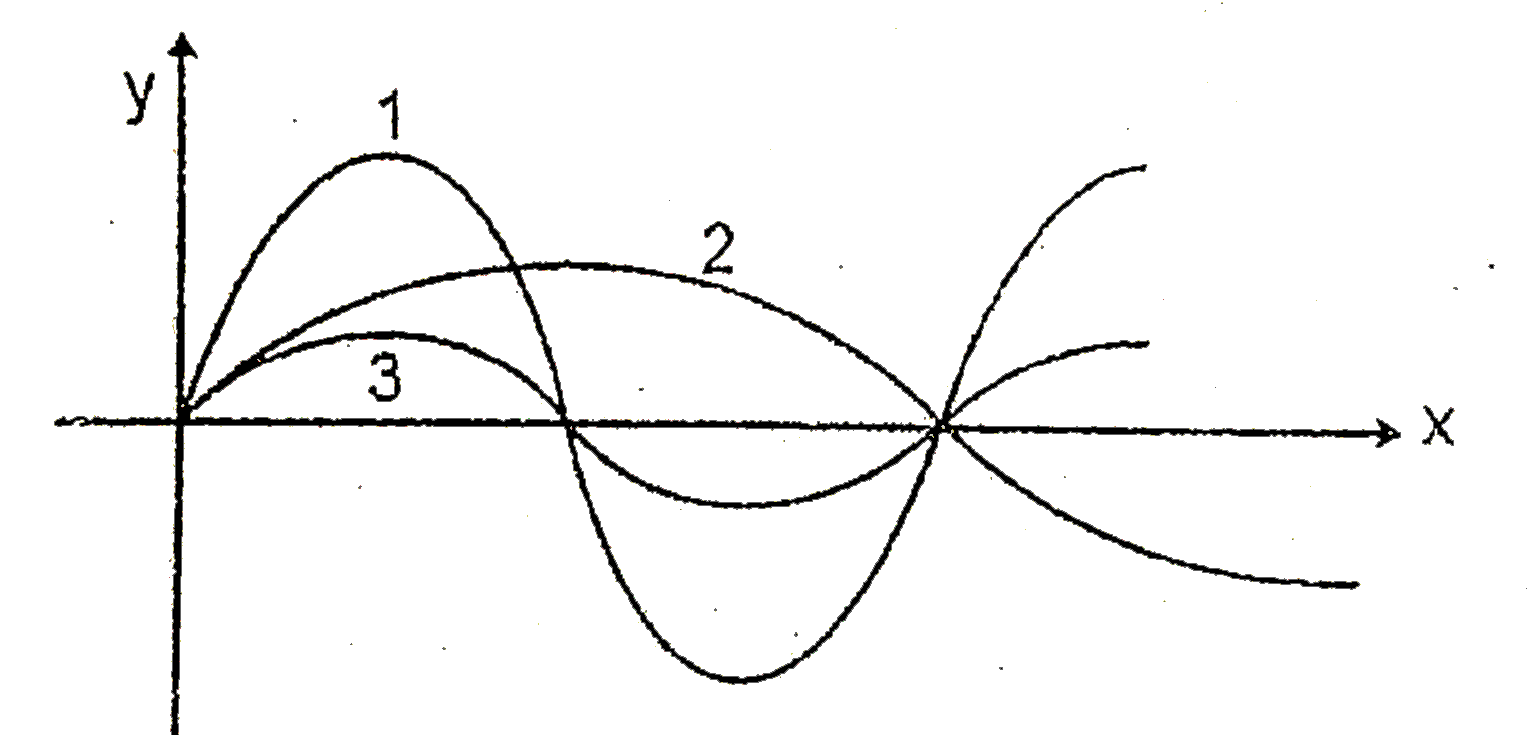
ω1=ω3>ω2
ω1>ω2>ω3
ω2>ω1=ω3
ω1=ω2=ω3
The correct Answer is:A
(A) As v=√Tμ is same for all, wave with maximum wavelength will have minimum angular frequency (by v=nλ). Also as λ1=λ2 thus ω1=ω2 hence (A)
Topper's Solved these Questions
Similar Questions
Graph shows three waves that are separately sent along a string that is stretched under a certain tension along x-axis. If ω1,ω2andω3 are their angular frequencies, respectively, then:

View SolutionGraph shows three waves that are separately sent along a string that is stretched under a certain tension along x-axis. If ω1,ω2andω3 are their angular frequencies, respectively, then:

View Solution
Knowledge Check
The stationary wave y = 2a sinkx cosωt in a stretched string is the result of superposition of y1=asin(kx−ωt) and
Ay2=acos(kx+ωt)By2=asin(kx+ωt)Cy2=acos(kx−ωt)Dy2=asin(kx−ωt)
Calculate the velocity of a transverse wave along a string of length 2m and mass 0.06kg under a tension of 500N.
View SolutionShow that the angle made by the string with the vertical in a conical pendulum is given by cosθ=gLω2 , where L is the string and ω is the angular speed.
View SolutionA block of weight W is supported by three strings as shown in figure. Which of the following relations is true for tension in the string ? (Here, T1,T2 and T3 are the tension in the strings A,B and C respectively)

View SolutionTwo strings of same material are stretched to the same tension . If their radii are in the ratio 1:2 , then respective wave velocities in them will be in ratio
View SolutionTwo discs of moments of inertia I1andI2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω1andω2 are brought into contact face to face with their axes of rotation coincident . What is the angular speed of the two-disc system ?
View SolutionTwo radio stations broadcast their programmes at the same amplitude A, and at slightly different frequencies ω1andω2 respectively , where ω2−ω1=103Hz. A detector receives the signals from the two stations simultaneously . It can emit signals only of intensity ≥2A2.
(i). Find the time intervals between successive maxima of the intensity of the signal received by the detector .
ii. Find the time for which the detector remains idle in each cycle of the intensity of the signal .
View SolutionTwo radio stations broadcast their programmes at the same amplitude A and at slightly different frequencies ω1 and ω2 respectively, where ω1−ω2=103Hz. A detector receives the signals from the two stations simultaneously, it can only detect signals of intensity ≥2A2.
(i) Find the time interval between successive maxima of the intensity of the signal received by the detector.
(ii) Find the time for which the detector remains idle in each cycle of the intensity of the signal.
View Solution
