Three particles A,B and C move in a circle in anticlockwise direction with speeds 1−1min,2.5ms−1 and 2ms−1 respectively. The initial positions of A,B and C are shown in fig. The ratio of distance travelled by B and C by the instant A,B and C meet for the first time is
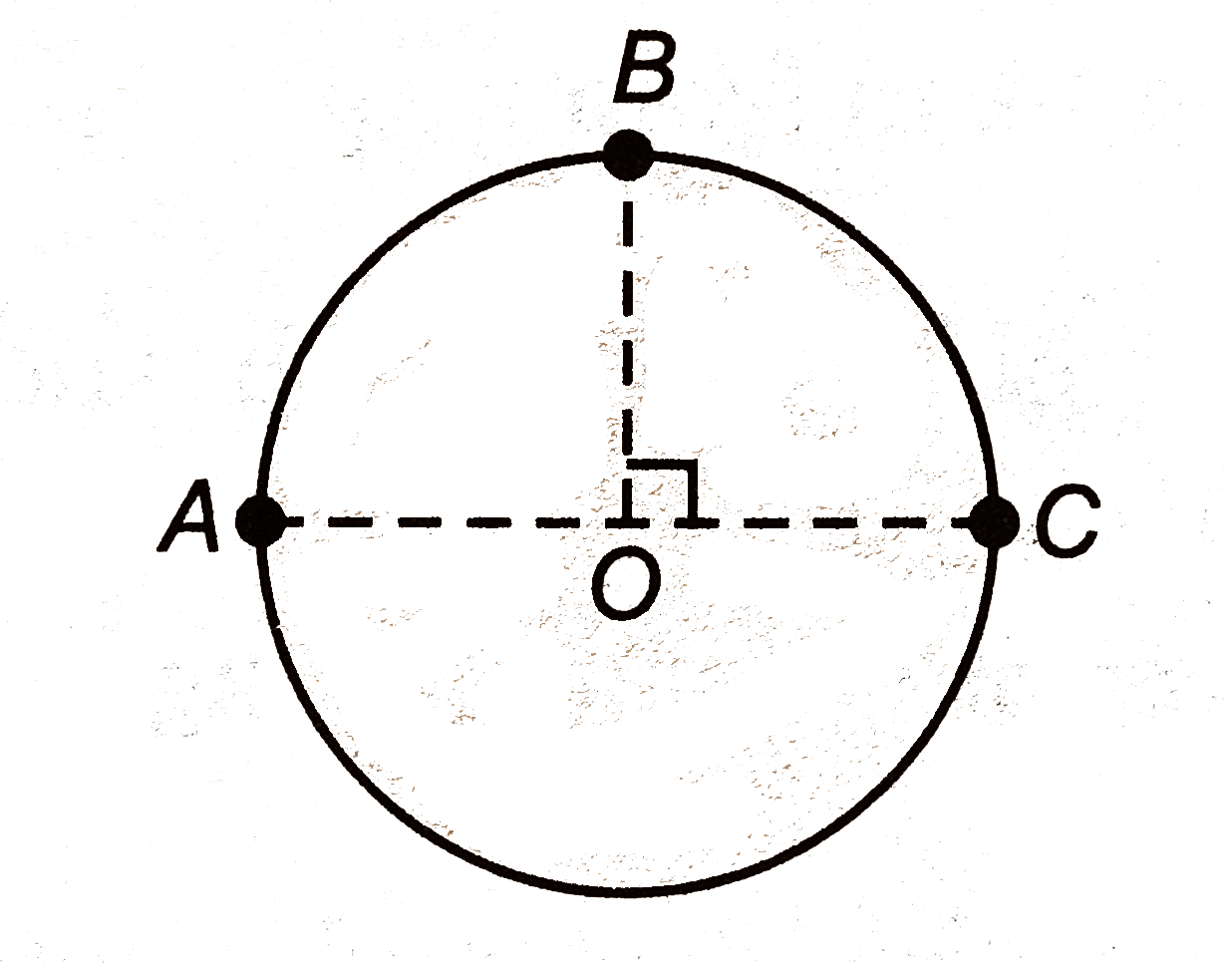
3:2
5:4
3:5
3:7
The correct Answer is:B
The ratio of distance travelled by B andC in same duration of time t is =vB:vC=5:4
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 42
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 43
11 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 40
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Three particles A, B and C move in a circle of radius r=1πm, in anti-clockwise direaction with speed 1ms−1,2.5ms−1 and 2ms−1 respectively. The initial position of A, B and C are as shown in figure.
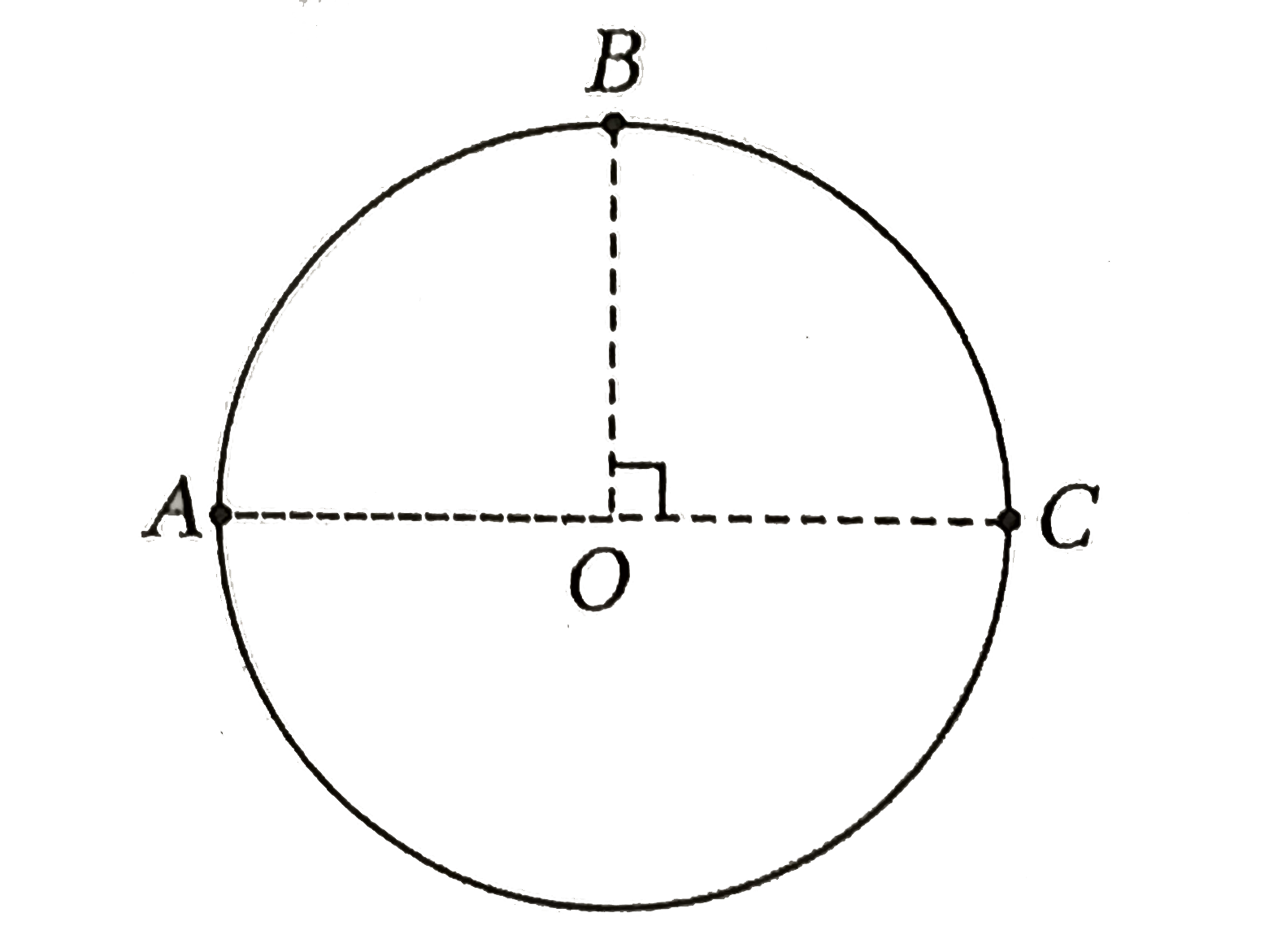
The ratio of distance travelled by B and C by the instant A, B and C meet for the first time is
View SolutionThree particles A,B and C move in a circle in anticlockwise direction with speeds 1−1min,2.5ms−1 and 2ms−1 respectively. The initial positions of A,B and C shown in figure . the ratio of distance travelled by A ,B and C by the instant they meet for the first time is
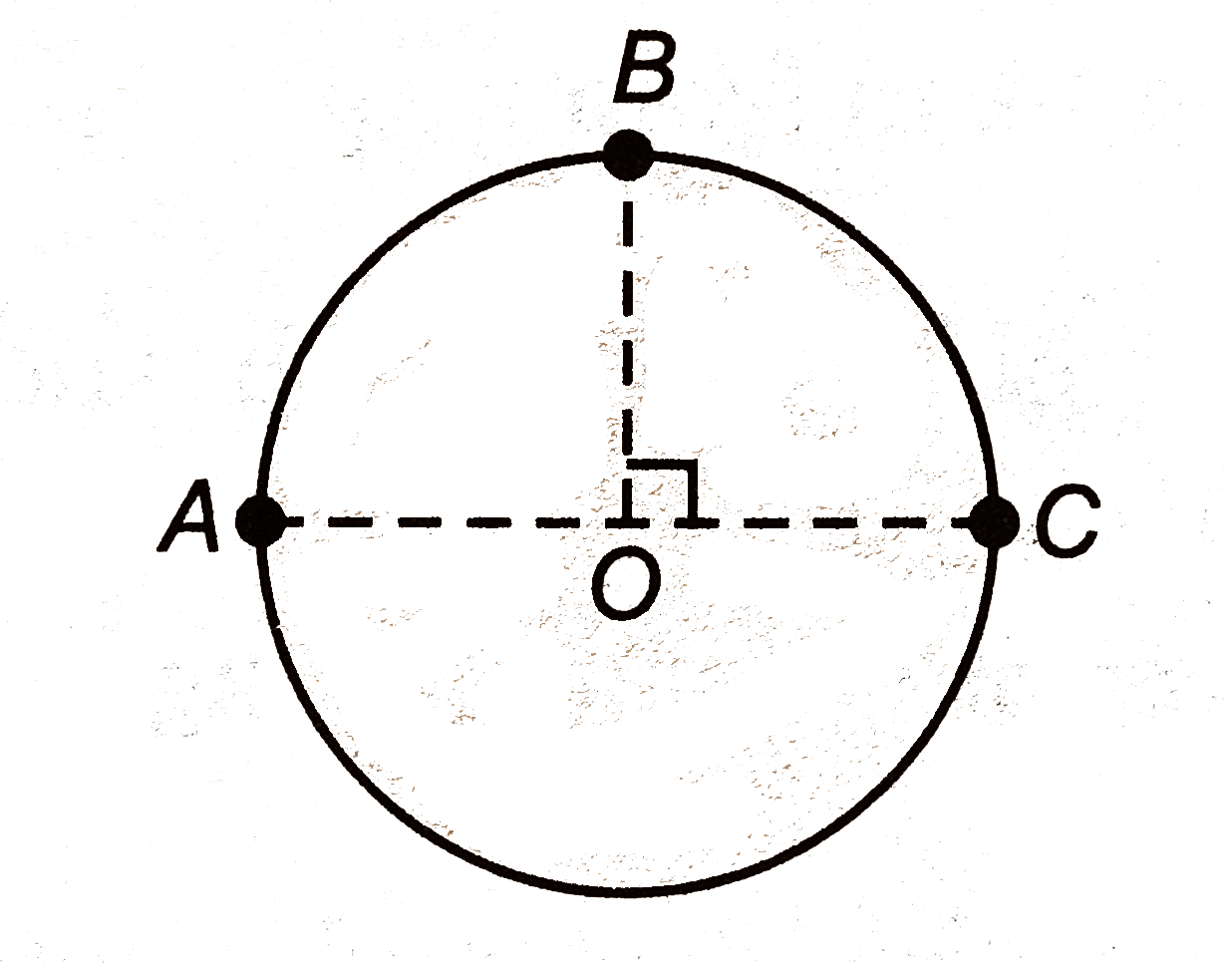
View SolutionBuses A and B are moving in the same direction with speed 20ms−1 and 15ms−1 respectively. Find the relative velcoity of A w.r.t. B and relative velocity of B w.r.t. A.
View SolutionThree particles of masses 1kg,2kg and 3kg are situated at the corners of an equilateral triangle move at speed 6ms−1,3ms−1 and 2ms−1 respectively. Each particle maintains a direction towards the particles at the next corners symmetrically. Find velocity of CM of the system at this instant

View SolutionTwo paricles A and B start at the origin O and travel in opposite directions along the circular path at constant speeds vA=0.7ms−1 and vB=1.0ms−1, respectively.
Determine the time when they collide and the magnitude of the acceleration of B just before this happens.

View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
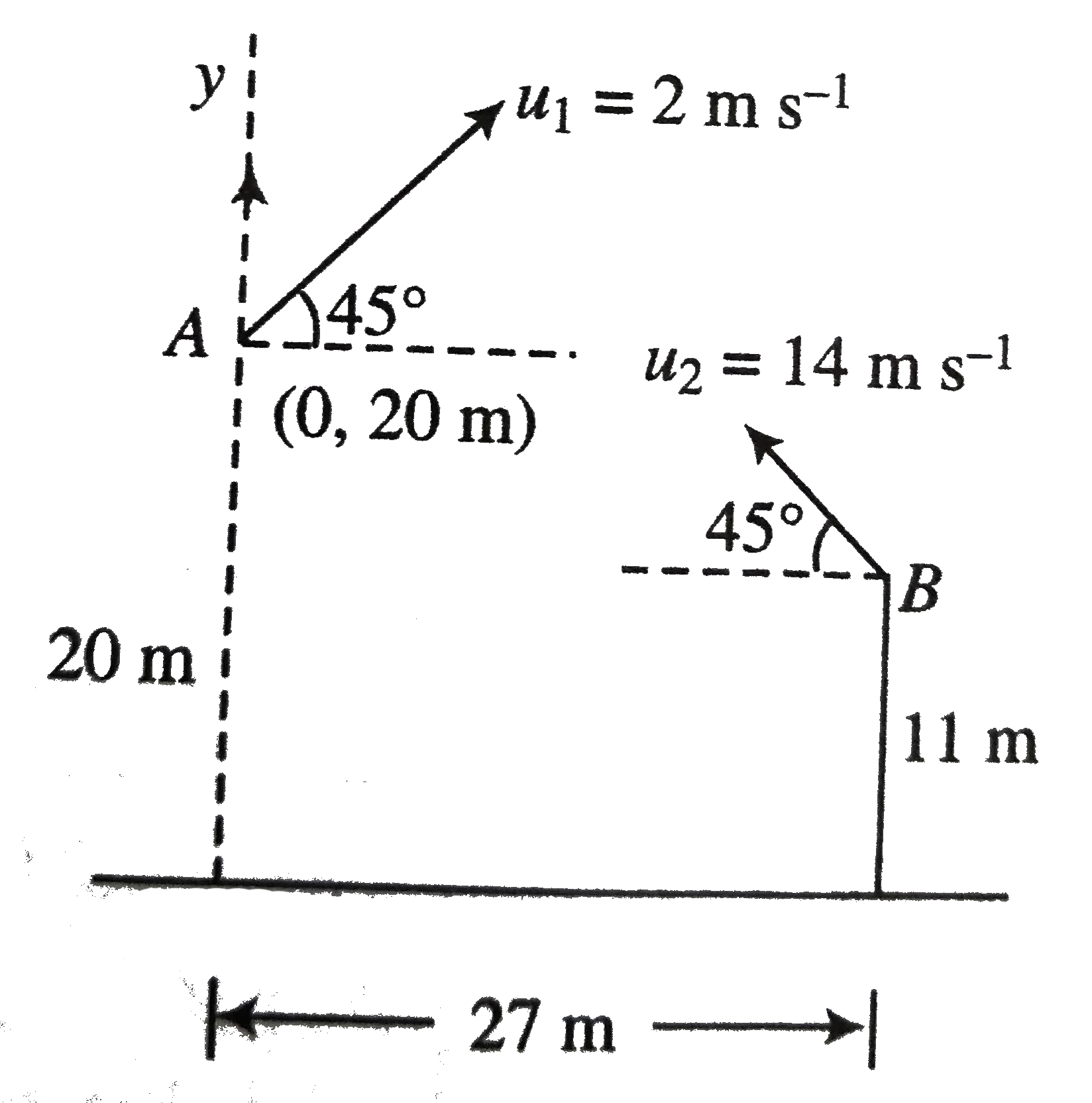
The relative velocity of B as seen from A in
View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
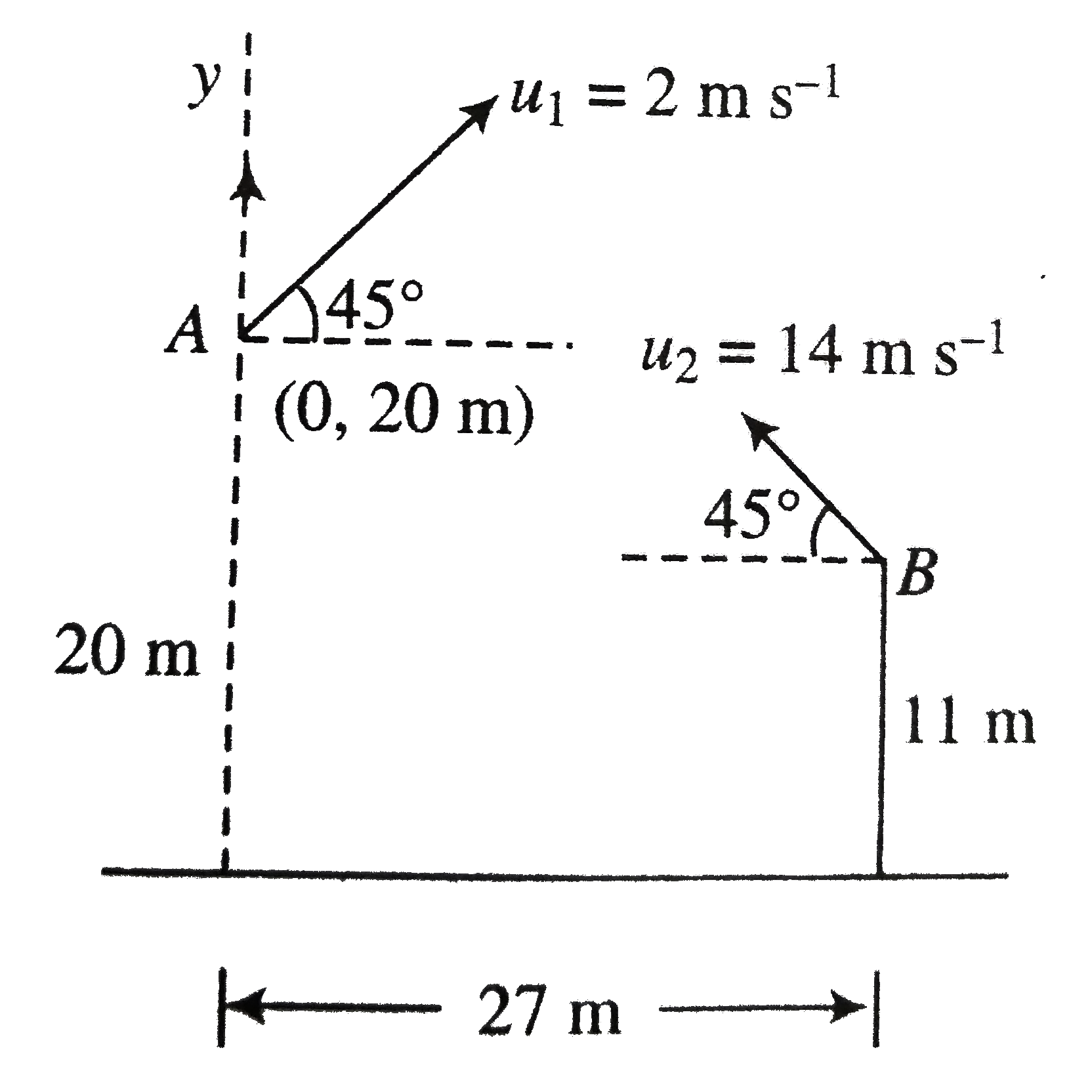
Minimum separation between A and B is
View SolutionThe velocities of A and B shown in fig. Find the speed (in ms−1) of block C. (Assume that the pulleys and string are ideal).

View SolutionTwo particles are moving in different circles in same plane with different angular velocities as shown in figure. At t = 0, initial positions of particles A and B are shown by dots on the respective circles. Initial distance between particles is 1m. Particle A move anticlockwise in the first circle whereas B moves clockwise in the second circle. Angle described (rotated) by A and B in time 't' are θA=(π2t) and θB=(πt) respectively. here θ is in radian and t is in second. Radius of each circle is shown in diagram.
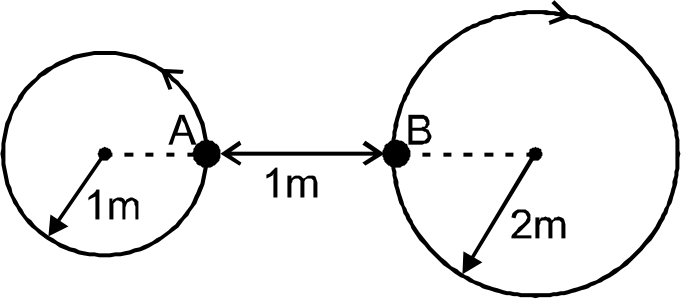
At time t=2 second, the angular velocity of the particle A with respect to the particle B is
View SolutionIf a and b are position vector of two points A,B and C divides AB in ratio 2:1, then position vector of C is
View Solution
