If Q=4v3+3v2, then the value of 'v' such that,there exist maxima of 'Q'-
0
−12
12
none
The correct Answer is:B
To find the value of v such that there exists a maximum of Q, we follow these steps:
1. Define the function: We have Q=4v3+3v2.
2. Differentiate Q: To find the critical points, we need to differentiate Q with respect to v.
dQdv=ddv(4v3+3v2)=12v2+6v
3. Set the derivative to zero: We set the first derivative equal to zero to find the critical points.
12v2+6v=0
4. Factor the equation: We can factor out 6v from the equation.
6v(2v+1)=0
5. Solve for v: Setting each factor equal to zero gives us:
6v=0⇒v=0
2v+1=0⇒v=−12
6. Determine the nature of the critical points: To check whether these points are maxima or minima, we need to find the second derivative of Q.
d2Qdv2=ddv(12v2+6v)=24v+6
7. Evaluate the second derivative at the critical points:
- For v=0:
d2Qdv2∣∣∣v=0=24(0)+6=6(which is >0, indicating a minima)
- For v=−12:
d2Qdv2∣∣∣v=−12=24(−12)+6=−12+6=−6(which is <0, indicating a maxima)
8. Conclusion: The value of v such that there exists a maximum of Q is:
v=−12
dQdv=ddv(4v3+3v2)=12v2+6v
12v2+6v=0
6v(2v+1)=0
6v=0⇒v=0
2v+1=0⇒v=−12
d2Qdv2=ddv(12v2+6v)=24v+6
- For v=0:
d2Qdv2∣∣∣v=0=24(0)+6=6(which is >0, indicating a minima)
- For v=−12:
d2Qdv2∣∣∣v=−12=24(−12)+6=−12+6=−6(which is <0, indicating a maxima)
v=−12
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 2 PHYSICS
1 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP NO. 5 Physics
6 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
An inverted L shaped conductor PRQ is made by joining two perpendicular conducting rods, each of length 1.5 L, at end R. This structure is moving in x-y plane containing variable magnetic field →B=−3xˆe(k) with a velocity vˆe(i)+vˆj. If potential of P is Vp and that of Q is VQ, then value of VP−V(Q) at the instant when P is at origin as shown in Fig. Will be

View SolutionIf the rms value of the voltage of the waveform shown below is √pqV , then what is the value of (p+q) ? (p and q are the smallest positive integers.)
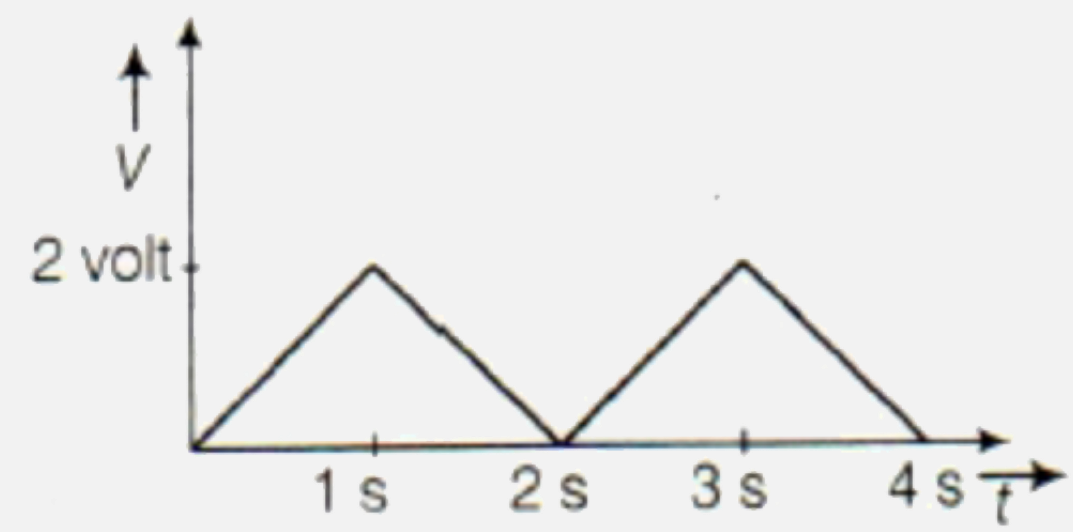
View Solution
Knowledge Check
A point moves with a uniform acceleration and v1,v2,v3 denote the average velociies in the three succellive intervals of time t1 ,t2 and t3. Find the ratio of ( v1 - v2) and ( v2 - v3).
At1−t2t2−t3Bt1−t3t2+t3Ct1+t2t2−t3Dt1+t2t2+t320u3v6(2)−15u2v10u4v+30u3v3
Which of the following is the reduced form of the expression above?A5uv40u7v4B2v−1u+2uv2C4uv−32u2+2uv2D2uv−3uv2u2+6
Given points P(2,3),Q(4,−2),andR(α,0) (i) Find the value of (ii)α(iii) (iv) if (v)(vi)PR+rQ(vii) (viii) is minimum (ix) Find the value of (x)α(xi) (xii) if (xiii)(ξv)|(xv)PR−RQ|(xvi) (xvii) is maximum
View SolutionConsider the following two statements:
P : If 7 is an odd number, then 7 is divisible by 2.
Q : If 7 is a prime number, then 7 is an odd number.
If V1 is the truth value of the contrapositive of P and V2 is the truth value of contrapositive of Q then the ordered pair (V1,V2) equals:
View SolutionIn the figure shown, the reading of voltmeters are V1=40V,V2=40V and V3=10V. Find
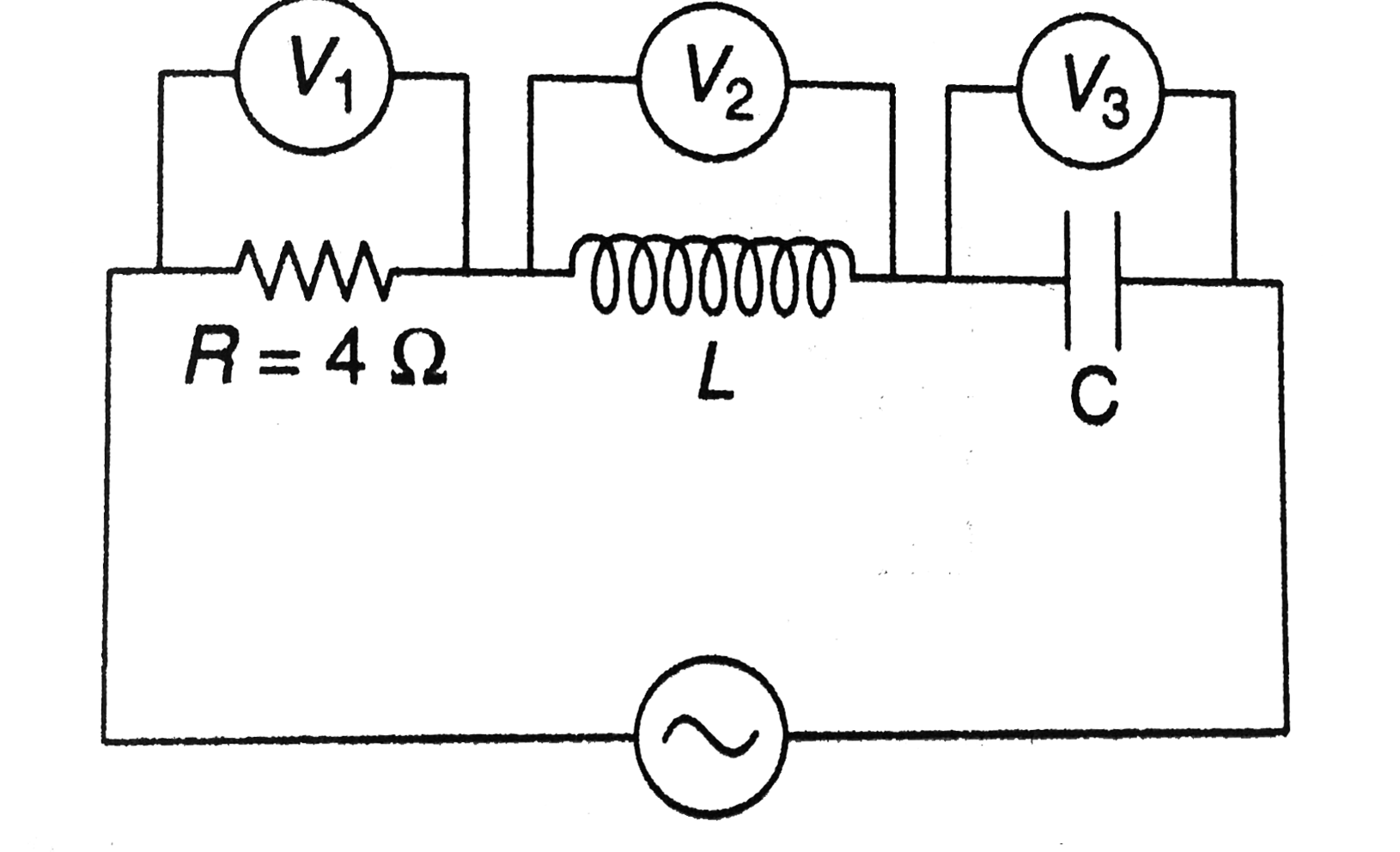
(a) the peak value of current
(b) the peak value of emf
(c) the value of L and C.
View SolutionLet →V1=ˆi+aˆj+ˆk,→V2=ˆj+aˆk and →V3=aˆi+ˆk,∀a>0. If [→V1→V2→V3] is minimum, then the value of a is
View SolutionIf p=9,v=3, then find p is terms of v from the equation dpdv=v+1v2
View SolutionIf the height and radius of a cone of volume V are doubled, then the volume of the cone, is (a) 3 V (b) 4 V (c) 6 V (d) 8 V
View Solution
