
A cylindrical diathemic chamber fitted with movable, massless & frictionless piston. Initially piston was at rest by the stop pin P as shown in figure. Compartment (A) is filled with 60g He gas & compartment (B) is filled with 96gofO2 gas ast 27∘C . Assume ideal behaviour of gas, then calculate ratio L1L2 , if stop pin is suddenly removed ? \
2
4
5
6
The correct Answer is:C

At equilibrium, FHe=FO2
nHeRTVHe×A=nO2RT×AVO2
nHeL1=nO2L2
∴L1L2=nHenO2=60/496/32=153=5
Similar Questions
In the figure, a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulated material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. The lower compartment of the container is filled with 2 moles of an ideal monoatomic gas at 700K and the upper compartment is filled with 2 moles of an ideal diatomic gas at 400K. The heat capacities per mole of an ideal monoatomic gas are CV=32R,CP=52R, and those for an ideal diatomic gas are CV=52R,CP=72R,

Consider the partition to be rigidly fixed so that it does not move. When equilibrium is achieved, the final temperature of the gasses will be
View SolutionIn the figure, a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulated material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. The lower compartment of the container is filled with 2 moles of an ideal monoatomic gas at 700K and the upper compartment is filled with 2 moles of an ideal diatomic gas at 400K. The heat capacities per mole of an ideal monoatomic gas are CV=32R,CP=52R, and those for an ideal diatomic gas are CV=52R,CP=72R,

Consider the partition to be rigidly fixed so that it does not move. When equilibrium is achieved, the final temperature of the gasses will be
View Solution
Knowledge Check
A monatomic ideal gas, initially at temperature T1 is enclosed in a cylinder fitted with a frictionless pistion. The gas is allowed to expand adiabatically to a temperature T2. By releasing the piston suddenly. IF L1 and L2 are th lengths of the gas column before and after expansion respectively, then T1/T2 is given by
A(L1/L2)2/3B(L1/L2)C(L2/L1)D(L2/L1)
A mixture of ethane (C2H6) and ethene (C2H4) occupies 40L at 1.00atm and at 400K. The mixture reacts completely with 130g of O2 to produce CO2 and H2O. Assuming ideal gas behaviour, calculate the mole fractions of C2H4 and C2H6 in the mixture.
View SolutionA mixture of ethane (C2H6) and ethene (C2H4) occupies 40L at 1.00atm and at 400K. The mixture reacts completely with 130g of O2 to produce CO2 and H2O. Assuming ideal gas behaviour, calculate the mole fractions of C2H4 and C2H6 in the mixture.
View SolutionA diatomic gas is enclosed in a vessel fitted with massless movable piston. Area of cross section of vessel is 1m2. Initial height of the piston is 1m (see the figure). The initial temperature of the gas is 300K. The temperature of the gas is increased to 400K, keeping pressure constant, calculate the new height of the piston. The piston is brought to its initial position with no heat exchange. Calculate the final temperature of the gas. You can leave answer in fraction.
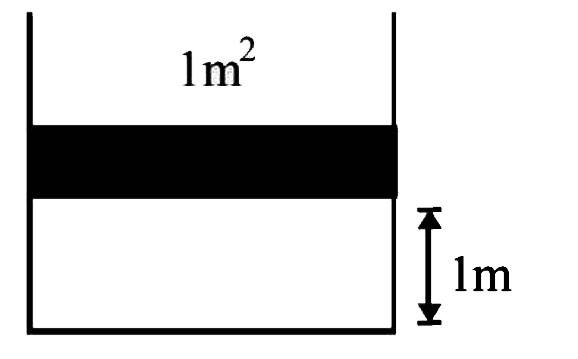
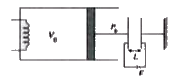
View SolutionAn ideal gas is enclosed in a cylinder fitted with a frictionless piston. The piston is connected with a light rod to one plate of capacitor whose other plate is fixed as shown. Initially volume of the gas inside the cylinder is V0 Atmospheric pressure is P0 separation between the plates is L, area of the piston as well as of the capacitor plates is A and emf of battery is ε . A heater supplies heat to the gas so that pressure of the gas is given as P=P0−nε0ε2L2 when piston is displaced by a distance L2 . Find value of n.
View SolutionA gas is enclosed in a cylindrical can fitted with a piston. The walls of the can and the piston are adiabatic. The initial pressure , volume and temperature of the gas are 100kPa,400cm3 and 300K respectively. The ratio of the specific heat capacities of the gas is (CpCv=1.5) Find the pressure and the temperature of the gas if it is (a) suddenly compressed (b) slowly compressed to 100cm3.
View SolutionFigure shows an adiabatic cylindrical tube of volume (V0) divided in two parts by a frictionless adiabatic separator . Initially, the separator is kept in the middle, an ideal gas at pressure (P1) and the temperatures (T1) is injected into the left part and the another ideal gas at pressures (P2) and temperature (T2) is injected into the right part. (CpCv=γ) is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find
(a) the volumes of the parts,
(b) the heat given to the gas in the left part and
(c) the final common pressure of the gases.

View SolutionWhen 2g of a gas A is introduced into an evacuated flask kept at 25∘C, the pressure is found to be one atmosphere. If 3 g of another gas B are then added to the same flask, the total pressure becomes 1.5 atm. Assuming ideal gas behaviour, calculate the ratio of molecular weights MA:MB.
View Solution
