A body is thrown vertically upwards with an initial velocity u. Write an expression for the maximum height attained by the body.
To derive the expression for the maximum height attained by a body thrown vertically upwards with an initial velocity u, we can follow these steps:
Step 1: Understand the motion
When the body is thrown upwards, it will rise until it reaches a maximum height where its velocity becomes zero. At this point, the body will start to fall back down.
Step 2: Identify the variables
- Initial velocity, u (upwards)
- Final velocity at maximum height, v=0 (the body stops momentarily)
- Acceleration due to gravity, g (acting downwards, hence it will be negative when considering the upward motion)
- Maximum height attained, h
Step 3: Use the kinematic equation
We can use the following kinematic equation that relates initial velocity, final velocity, acceleration, and displacement (height in this case):
v2=u2+2as
Where:
- v is the final velocity (0 m/s at maximum height)
- u is the initial velocity
- a is the acceleration (which will be −g when moving upwards)
- s is the displacement (which is the maximum height h)
Step 4: Substitute the known values
Substituting the known values into the equation:
02=u2+2(−g)h
This simplifies to:
0=u2−2gh
Step 5: Rearrange the equation
Rearranging the equation to solve for h:
2gh=u2
h=u22g
Conclusion
The expression for the maximum height h attained by the body when thrown vertically upwards with an initial velocity u is:
h=u22g
When the body is thrown upwards, it will rise until it reaches a maximum height where its velocity becomes zero. At this point, the body will start to fall back down.
- Initial velocity, u (upwards)
- Final velocity at maximum height, v=0 (the body stops momentarily)
- Acceleration due to gravity, g (acting downwards, hence it will be negative when considering the upward motion)
- Maximum height attained, h
We can use the following kinematic equation that relates initial velocity, final velocity, acceleration, and displacement (height in this case):
v2=u2+2as
Where:
- v is the final velocity (0 m/s at maximum height)
- u is the initial velocity
- a is the acceleration (which will be −g when moving upwards)
- s is the displacement (which is the maximum height h)
Substituting the known values into the equation:
02=u2+2(−g)h
This simplifies to:
0=u2−2gh
Rearranging the equation to solve for h:
2gh=u2
h=u22g
The expression for the maximum height h attained by the body when thrown vertically upwards with an initial velocity u is:
h=u22g
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - 3(E) (Multiple choice type)
5 Videos
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - 3(E) (Numericals)
31 Videos
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - 3(D) (Numerical)
3 Videos
- ICSE ANNUAL EXAMINATION -2020BOOK - ICSECHAPTER - ICSE ANNUAL EXAMINATION -2020EXERCISE - SECTION-II
45 Videos
- LIGHTBOOK - ICSECHAPTER - LIGHTEXERCISE - TOPIC 2 Spherical Mirrors (4 Marks Questions )
9 Videos
Similar Questions
Two bodies are thrown vertically upwards with their initial velocity in the ratio 2:3. Then the ratio of the maximum height attained by them is
View SolutionA body is thrown vertically upwards with initial velocity 'u' reaches maximum height in 6 seconds. The ratio of distances travelled by the body in the first second and seventh second is
View Solution
Knowledge Check
A stone is thrown vertically upwards with an initial velocity u form the top of a tower, recahes the ground with a velocity 3u. The height of the tower is
A3u2gB4u2gC6u2gD9u2g
A body A is thrown vertically upwards with such a velocity that it reaches a maximum height of h. Simultaneously, another body B is dropped from height h. It strikes the ground and does not rebound. The velocity of A relative to B versus time graph is best represented by (upward direction is positive).
View SolutionA body of mass m1 projected vertically upwards with an initial velocity 'u' reaches a maximum height 'h'. Another body of mass m2 is projected along an inclined plane making an angle 30∘ with the horizontal and with speed 'u'. The maximum distance travelled along the incline is
View SolutionA ball is thrown vertically upward with a velocity of 20 m/s. Calculate the maximum height attain by the ball.
View SolutionA rocket is projected vertically upwards and its time velocity graph is shown in the figure-1.115. The maximum height attained by the rocket is :
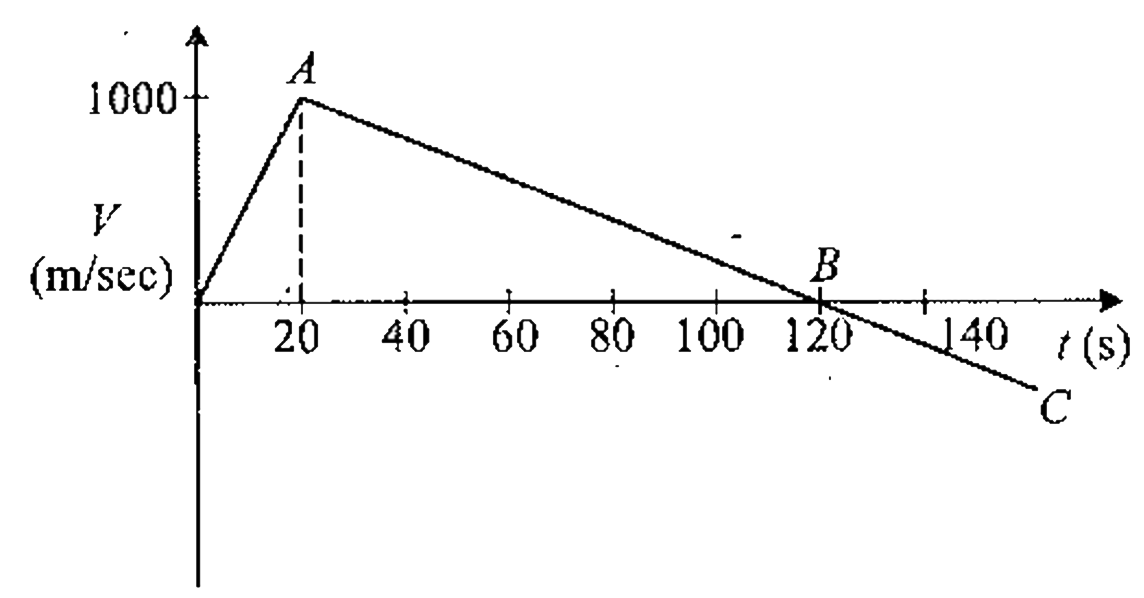
View SolutionA particle is thrown vertically upwards. If its velocity is half of the maximum height is 20m/s, then maximum height attained by it is
View SolutionA body is thrown vertically upwards which graph represents variation of velocity w.r.t time
View SolutionA body is thrown vertically up with certain velocity. If h is the maximum height reached by it, its position when its velocity reduces to 1/3 of its velocity of projection is at
View Solution
