For the combination of resistors shown in Fig. find the equivalent resistance between the points
C and D

Between the points C and D: The resistors R2,R3 and R4 are in series. They can be replaced by an equivalent resistance Rs, where
Rs=R2+R3+R4=3+3+3=9Ω.
The resistance R5(=3Ω)andRs(=9Ω) are in parallel between the points C and D as shown in Fig.

If the equivalent resistance between C and D in Fig. is Rp, then
1Rp=13+19or1Rp=3+19=49
orRp=94=2.25Ω
Thus the equivalent resistance between C and D is 2.25 Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(A)
43 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(A) ( MULTIPLE CHOICE TYPE)
2 Videos
- CALORIMETRYBOOK - ICSECHAPTER - CALORIMETRYEXERCISE - EXERCISE-11(B) (NUMERICALS)
15 Videos
- ELECTRO-MAGNETISM BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10 (C) NUMERICALS
1 Videos
Similar Questions
For the combination of resistors shown in Fig. find the equivalent resistance between the points
A and B

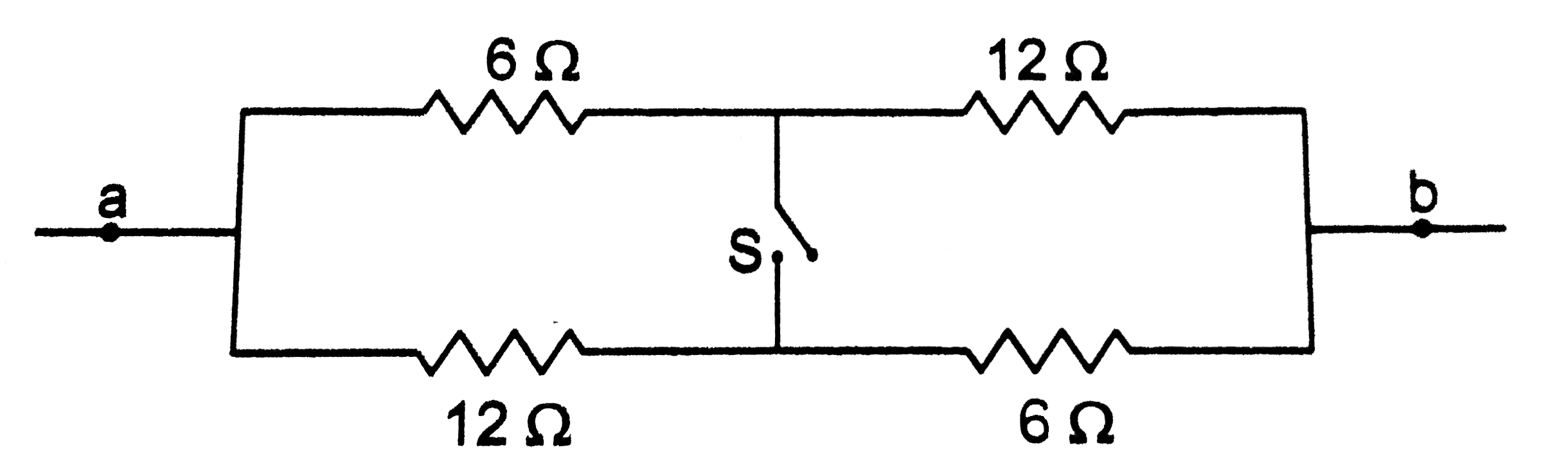
View SolutionFind the equivalent resistance between the point a and b .
View SolutionFind the equivalent resistance between points A and B

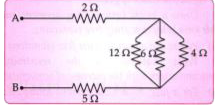
View SolutionFind the equivalent resistance between points A and B.
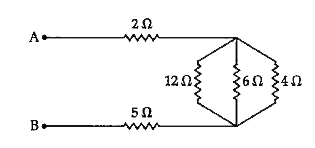
View SolutionFind the equivalent resistance between points A and B.
View SolutionFind the the equivalent resistance between points A and B.

View SolutionFind equivalent resistance between A and D
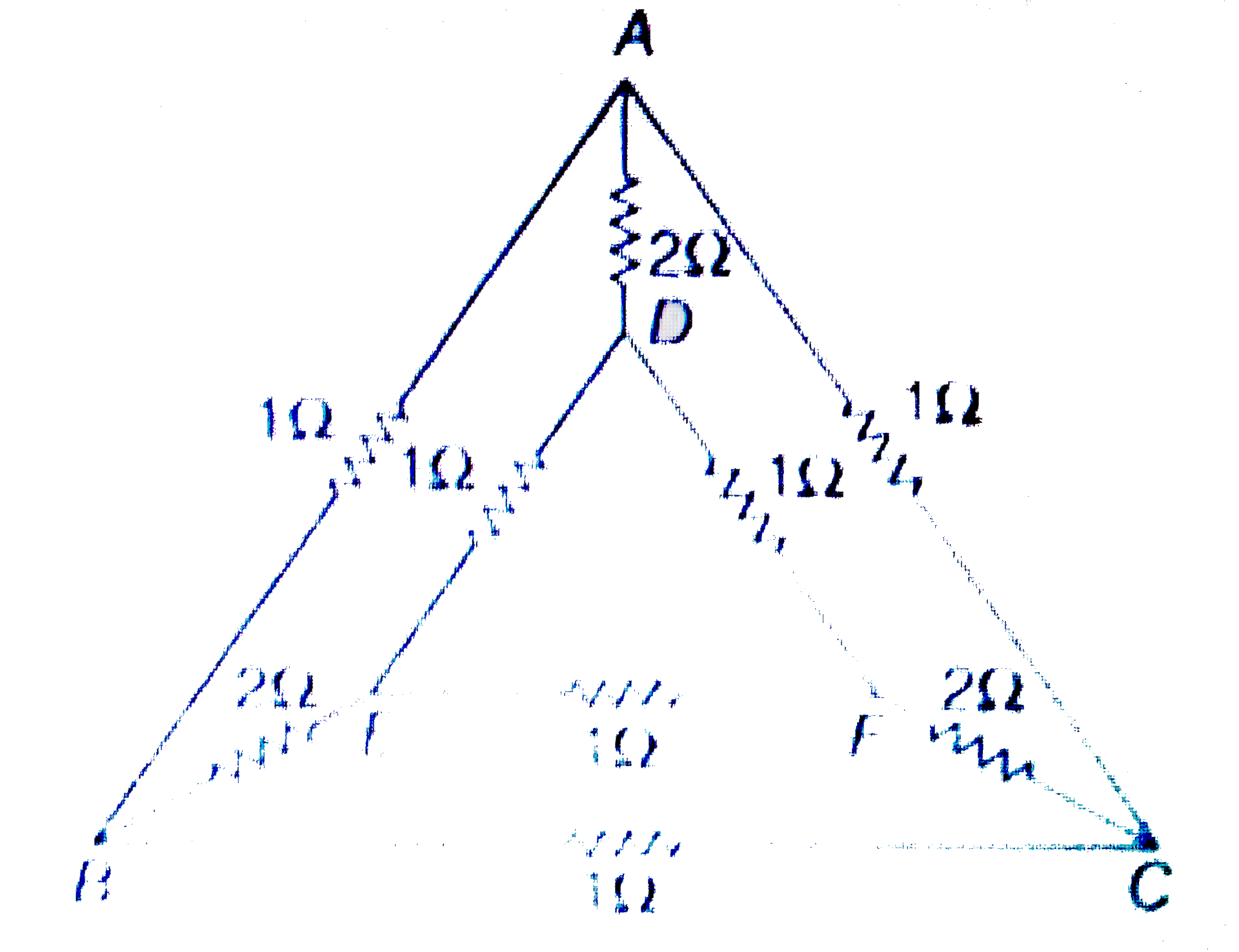
View SolutionIn the network shown in Fig., calculate the equivalent resistance between the points
A and C.
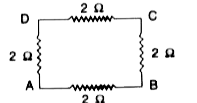
View SolutionIn the network shown in Fig., calculate the equivalent resistance between the points
A and B,
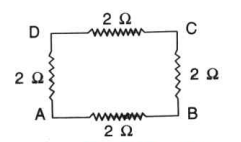
View SolutionIn the circuit shown in Fig. (b) calculate the equivalent resistance between the points A and B.
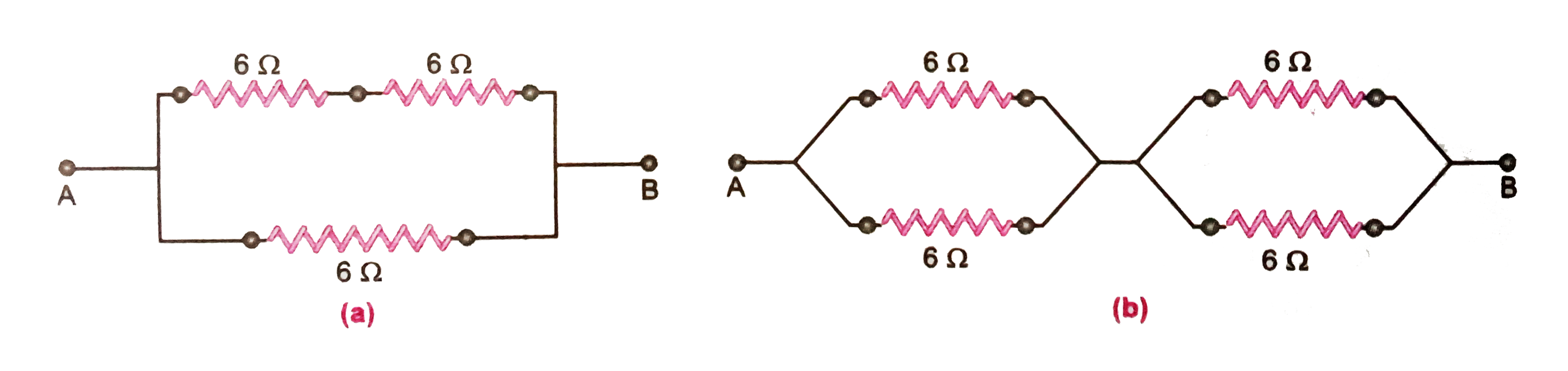
View Solution
