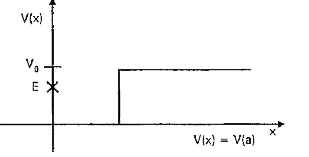
Given in Fig. are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any in which the particle cannot be found for the given energy. Also , indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant
 Solution in Telugu
Solution in Telugu
We know that total energy E = P.E + K.E (or) K.E = E - P.E and K.E can never by negative . The object cannot exist in the region where its E.E would become negative
(i) For x<a, P.E (v0)>E
∴K.E becomes negative. Hence the object cannot exist in the region x>a
(ii) For x<aandx>b,P.E(v0)>E
∴ K.E becomes negative. Hence the object cannot be present in the region x>aandx>b
(iii) Object cannot exist in any region because P.E(v0)>E in every region
(iv) On the same basis, the object cannot exist in the region −b/2<x<−a/2anda/2<x<b/2
Similar Questions
चित्र में कुछ एकविमीय स्थितिज ऊर्जा - फलनों के उदाहरण दिए गए हैं । कण की कुल ऊर्जा कोटि - अक्ष पर क्रॉस द्वारा निर्देशित की गई है । प्रत्येक स्थिति में, कोई ऐसे क्षेत्र बताइए, यदि कोई हैं तो, जिनमें दी गई ऊर्जा के लिए, कण को नहीं पाया जा सकता । इसके अतिरिक्त, कण की कुल न्यूनतम ऊर्जा भी निर्देशित कीजिए । कुछ ऐसे भौतिक संदर्भो के विषय में सोचिए जिनके लिए ये स्थितिज ऊर्जा आकृतियाँ प्रासंगिक हों ।
(c)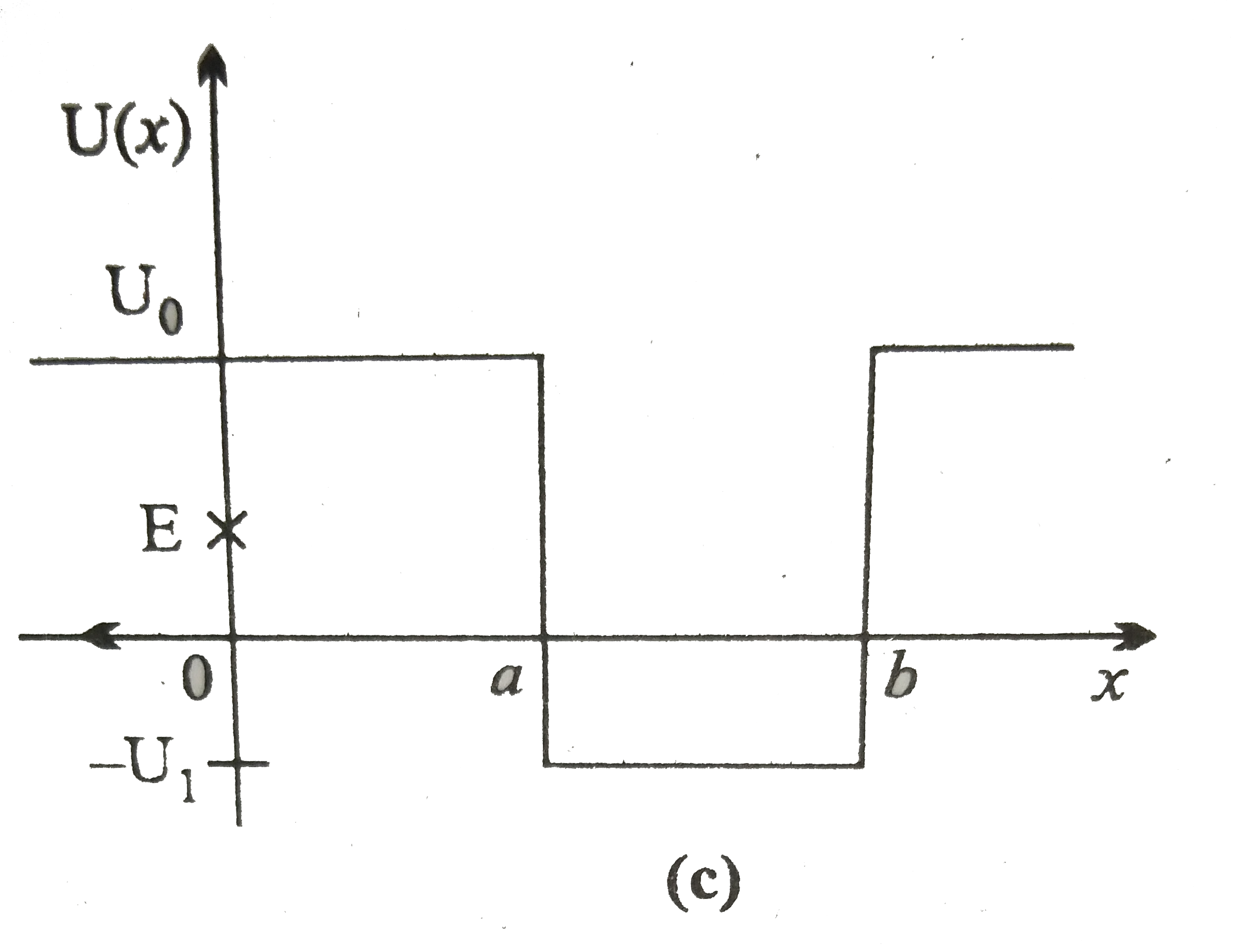
View Solutionचित्र में कुछ एकविमीय स्थितिज ऊर्जा - फलनों के उदाहरण दिए गए हैं । कण की कुल ऊर्जा कोटि - अक्ष पर क्रॉस द्वारा निर्देशित की गई है । प्रत्येक स्थिति में, कोई ऐसे क्षेत्र बताइए, यदि कोई हैं तो, जिनमें दी गई ऊर्जा के लिए, कण को नहीं पाया जा सकता । इसके अतिरिक्त, कण की कुल न्यूनतम ऊर्जा भी निर्देशित कीजिए । कुछ ऐसे भौतिक संदर्भो के विषय में सोचिए जिनके लिए ये स्थितिज ऊर्जा आकृतियाँ प्रासंगिक हों ।
(d)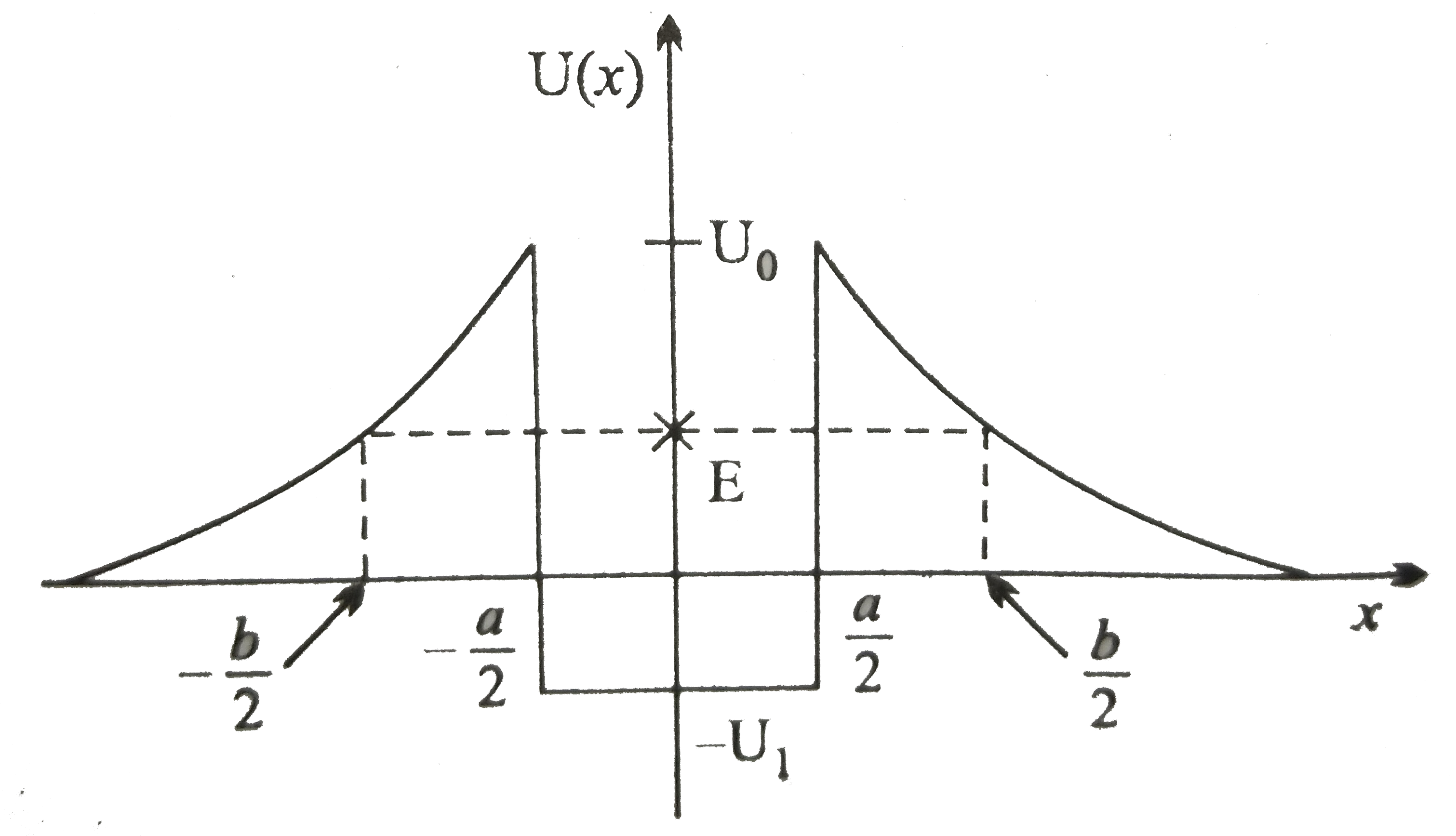
View Solutionएक कण सरल आवर्त गति कर रहा है। किस स्थिति में
स्थितिज ऊर्जा कुल ऊर्जा की एक चौथाई होगी ?
View SolutionConsider a one - dimensional motion a a particle with total energy E . There are four regions A,B,C and D in which the relation between potential energy V , kinetic energy (K) and total energy E is as given ahead :
State with reason in each case whether a particle can be found in the given region or not .
View SolutionGiven in Fig. are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
View SolutionGiven in Fig. 6.11 are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
View SolutionGiven in Fig. 6.11 are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
View Solutionसरल आवृत गति करते हुए किसी कण की कुल ऊर्जा (x = विस्थापन) है तो उस कण की कुल ऊर्जा होगी।
View Solution
