A vector is not changed if
Frame of reference is translated
Vector is translated parallel to itself
Vector is rotated
Both (A) and (B)
The correct Answer is:D
To determine when a vector is not changed, we need to analyze the conditions provided in the question. A vector is defined by both its magnitude and direction. Therefore, for a vector to remain unchanged, both of these properties must remain constant.
1. Understanding the Vector:
A vector has both magnitude (length) and direction. For a vector to remain unchanged, both these aspects must not vary.
2. Analyzing Option 1: Frame of Reference is Translated:
- When we translate the frame of reference, we are essentially moving the entire coordinate system without altering the vector itself.
- The direction and magnitude of the vector remain the same because we are just shifting our perspective.
- Conclusion: The vector does not change in this case.
3. Analyzing Option 2: Vector is Translated Parallel to Itself:
- Translating a vector parallel to itself means moving it without changing its direction.
- For example, if we move the vector up or down while keeping it parallel, its magnitude and direction remain unchanged.
- Conclusion: The vector does not change in this case either.
4. Analyzing Option 3: Vector is Rotated:
- Rotating a vector means changing its direction while keeping its magnitude the same.
- If we rotate the vector, it points in a new direction, which means it has changed.
- Conclusion: The vector does change in this case.
5. Final Evaluation:
- From the analysis, we find that options 1 and 2 do not change the vector, while option 3 does change it.
- Therefore, the correct answer is that both options 1 and 2 are correct, leading us to option 4, which states that both A and B are correct.
Final Answer:
The vector is not changed if:
- A) The frame of reference is translated.
- B) The vector is translated parallel to itself.
- Therefore, the correct option is 4) Both A and B are correct.
A vector has both magnitude (length) and direction. For a vector to remain unchanged, both these aspects must not vary.
- When we translate the frame of reference, we are essentially moving the entire coordinate system without altering the vector itself.
- The direction and magnitude of the vector remain the same because we are just shifting our perspective.
- Conclusion: The vector does not change in this case.
- Translating a vector parallel to itself means moving it without changing its direction.
- For example, if we move the vector up or down while keeping it parallel, its magnitude and direction remain unchanged.
- Conclusion: The vector does not change in this case either.
- Rotating a vector means changing its direction while keeping its magnitude the same.
- If we rotate the vector, it points in a new direction, which means it has changed.
- Conclusion: The vector does change in this case.
- From the analysis, we find that options 1 and 2 do not change the vector, while option 3 does change it.
- Therefore, the correct answer is that both options 1 and 2 are correct, leading us to option 4, which states that both A and B are correct.
The vector is not changed if:
- A) The frame of reference is translated.
- B) The vector is translated parallel to itself.
- Therefore, the correct option is 4) Both A and B are correct.
Topper's Solved these Questions
Similar Questions
(A): The direction of velocity vector remains unchanged though the coordinate system is changed
(R) : The direction of real vector is independent of coordinate system
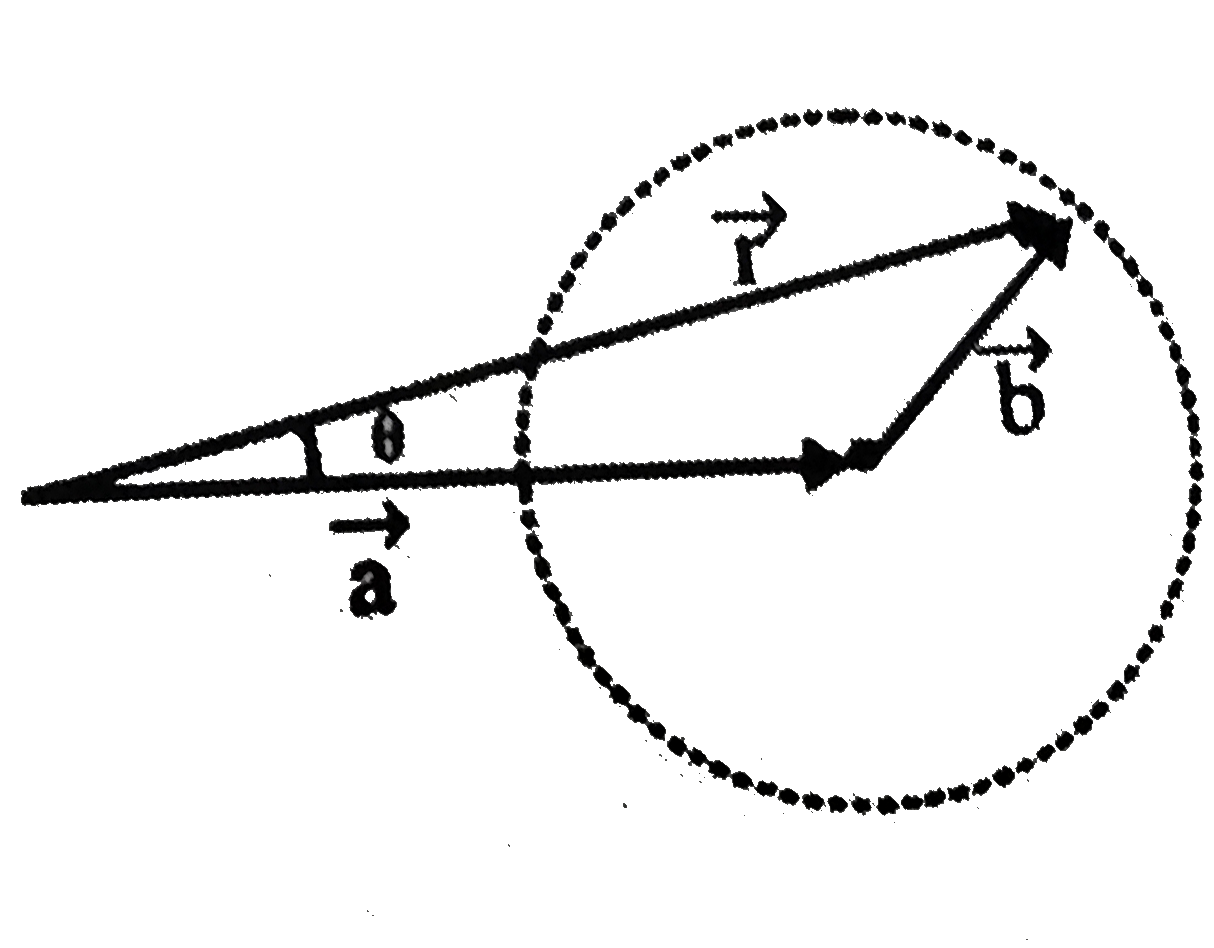
View SolutionKeeping one vector constant, if direction of other to be added in the first vector is changed continuously, tip of the resultant vector describes a circles, In the following figure vector →a is kept constant. When vector →b addede to →a changes its direction, the tip of the resultant vector →r=→a+→b describes circles of radius b with its centre at the tip of vector →a. Maximum angle between vector →a and the resultant →r=→a+→b is
View Solution
Knowledge Check
An impulse is supplied to a moving object with the force at an angle of 120∘ with respect to velocity vector. The angle between the impulse vector and the change in momentum vector is
A120∘B0∘C60∘D240∘
Asserion: Magnitude of the resultant of two vectors may be less than the magnitude of either vector.
Reason: The resultant of two vectors is obtained by means of law of parallelogram of Vectors.
View SolutionA vector may change when we :
View SolutionA vector may change when we :
View SolutionAssertion : Acceleration of a moving particle can change its direction without any change in direction of velocity.
Reason : If the direction of change in velocity vector changes, the direction of acceleration vector also changes.
View SolutionAssertion : Acceleration of a moving particle can change its direction without any change in direction of velocity.
Reason : If the direction of change in velocity vector changes, the direction of acceleration vector also changes.
View SolutionA vector →a is turned without a change in its length through a small angle dθ. Find the value of |Δ→a|
View SolutionA vector →a is turned without a change in its length through a small angle dθ. Find the value of |Δ→a|
View Solution
