Two pistons of a hydraulic machine have diameters of 30.0 cm and 2.5 cm. What is the force exerted on the larger piston when 40 kg wt. is placed on the smaller piston? If the smaller piston moves in through 6 cm, how much does the other piston move out ?
To solve the problem, we will follow these steps:
Step 1: Calculate the Force on the Larger Piston
Given:
- Diameter of the larger piston, D1=30.0cm
- Diameter of the smaller piston, D2=2.5cm
- Weight on the smaller piston, F1=40kg
First, we need to convert the weight into Newtons (since 1kg weight = 9.81N):
F1=40kg×9.81m/s2=392.4N
Using Pascal's law, we know:
F1A1=F2A2
Where A1 and A2 are the areas of the larger and smaller pistons, respectively.
The area of a circle is given by:
A=π4D2
So,
A1=π4D21=π4(30cm)2=π4(900)=225πcm2
A2=π4D22=π4(2.5cm)2=π4(6.25)=1.5625πcm2
Now, substituting A1 and A2 into Pascal's law:
F2=F1⋅A2A1=392.4⋅1.5625π225π
The π cancels out:
F2=392.4⋅1.5625225
Calculating this gives:
F2=392.4⋅0.006944≈2.73N
Step 2: Calculate the Distance Moved by the Larger Piston
Given that the smaller piston moves down by x2=6cm, we need to find x1 (the distance the larger piston moves up).
Using the principle of conservation of volume in an incompressible fluid:
A1x1=A2x2
Rearranging gives:
x1=A2A1x2
Substituting the areas:
x1=1.5625π225π⋅6
The π cancels out again:
x1=1.5625225⋅6
Calculating this gives:
x1=0.042cm or 0.42mm
Final Answers:
1. The force exerted on the larger piston is approximately 2.73N.
2. The distance the larger piston moves out is approximately 0.042cm or 0.42mm.
Given:
- Diameter of the larger piston, D1=30.0cm
- Diameter of the smaller piston, D2=2.5cm
- Weight on the smaller piston, F1=40kg
F1=40kg×9.81m/s2=392.4N
F1A1=F2A2
Where A1 and A2 are the areas of the larger and smaller pistons, respectively.
A=π4D2
So,
A1=π4D21=π4(30cm)2=π4(900)=225πcm2
A2=π4D22=π4(2.5cm)2=π4(6.25)=1.5625πcm2
F2=F1⋅A2A1=392.4⋅1.5625π225π
The π cancels out:
F2=392.4⋅1.5625225
Calculating this gives:
F2=392.4⋅0.006944≈2.73N
Given that the smaller piston moves down by x2=6cm, we need to find x1 (the distance the larger piston moves up).
A1x1=A2x2
Rearranging gives:
x1=A2A1x2
x1=1.5625π225π⋅6
The π cancels out again:
x1=1.5625225⋅6
Calculating this gives:
x1=0.042cm or 0.42mm
1. The force exerted on the larger piston is approximately 2.73N.
2. The distance the larger piston moves out is approximately 0.042cm or 0.42mm.
Similar Questions
Two pistons of a hydraulic machine have diameters of 30.0 cm and 2.5 cm. What is the force exerted on the larger piston when 40 kg wt. is placed on the smaller piston? If the smaller piston moves in through 6 cm, how much does the other piston move out ?
View SolutionTwo syringes of different cross-sections (without needles) filled with water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston and larger piston are 1.0cm and 3.0 cm respectively.
(a) Find the force on the larger piston when a force of 10N is applied to the smaller piston.
(b) The smaller piston is paused in through 6.0 cm, much does the larger piston move out?
View Solution
Knowledge Check
In the previous question if the smaller piston is pushed in through 6cm, how much does the longer piston move out?
A23 cmB32 cmC13 cmD12 cmTwo syringes of different cross-section (without needle filled with water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston an larger piston are 1cm and 3cm respectively. If a force of 10N is applied to the smaller piston then the force exerted on the larger piston is
A30NB60 NC90 ND100 N
In an arrangement similar to a hydraulic lift, the diameters of smaller and larger pistons are 1.0 cm and 3.0 cm respectively. What is the force exerted on the larger piston when a force of 10 N is applied to the smaller piston?
View SolutionThe areas of pistons in a hydraulic machine are 5cm2 and 625cm2. What force on the smaller piston will support a load of 1250 N on the larger piston ? State any assumption which you make in your calculation.
View SolutionThe pressure exerted on the smaller and the larger piston of a hydraulic machine is 15 Pa Calculate the force exerted by it on the larger piston, if the area of cross section of the larger piston is 4m2.
View SolutionA force of 50 kgf is applied to the smaller piston of a hydraulic machine. Neglecting friction, find the force exerted on the large piston, if the diameters of the pistons are 5 cm and 25 cm respectively.
View SolutionFigure shown a hydraulic press with the larger piston if diameter 35 cm at a height of 1.5 cm at a height of 1.5 m relative to the smaller piston of diameter 10cm. The mass on the smaller piston is 20 kg. What is the force exerted on the load by the larger piston? The density of oil in the press is 750kh/m3 . (Take g=9.8m/s2)
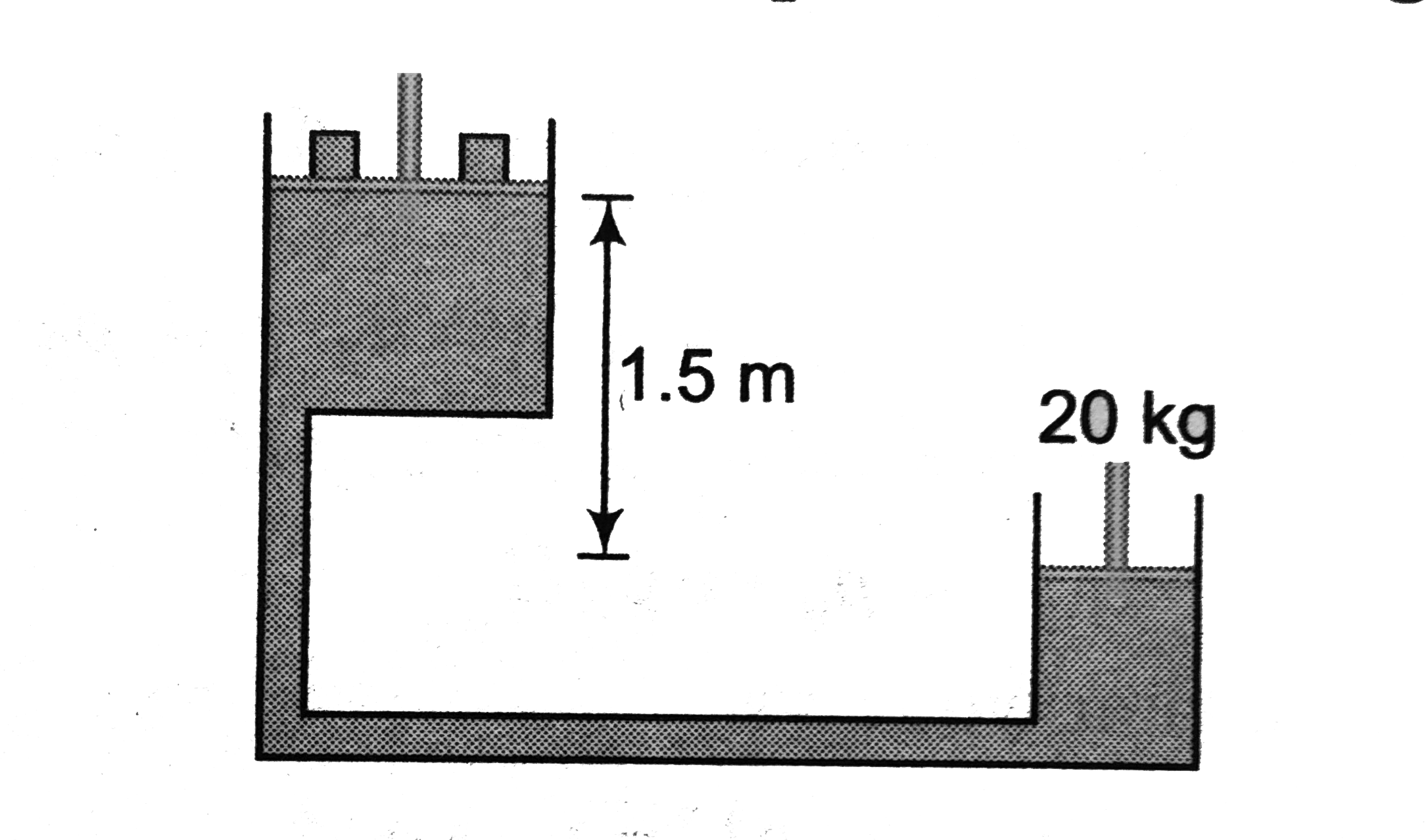 .
.
View SolutionFigure shown a hydraulic press with the larger piston if diameter 35 cm at a height of 1.5 m relative to the smaller piston of diameter 10cm. The mass on the smaller piston is 20 kg. What is the force exerted on the load by the larger piston? The density of oil in the press is 750kh/m3 . (Take g=9.8m/s2)
 .
.
View Solution
