We know that the slopes of two parallel lines are equal. If two lines having the same slope pass through a common point, then they will coincide. Hence, If A, B and C are three points in the XY-plane, then they will lie on a line i.e. three points are collinear if and only if slope of AB=slope of BC.

Let (a,0),B(0,b)andC(x,y) be the given collinear points, then,
Slope of Ab= Slope of BC
⇒b−00−a=y−bx−0
⇒−ba=y−bx
−bx=ay−ab
⇒bx+=ay−ab
⇒xa+yb=1.
Hence Proved.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - TRY YOURSELF23videos
STRAIGHT LINES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ASSIGNMENT (SECTION A) (OBJECTIVE TYPE QUESTIONS) (ONLY ONE ANSWER)50videos
STRAIGHT LINES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STATISTICSEXERCISE - Section-C Assertion-Reason15videos
STATISTICS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - J10videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
If the figure, what is the slope of line passing through the two points?
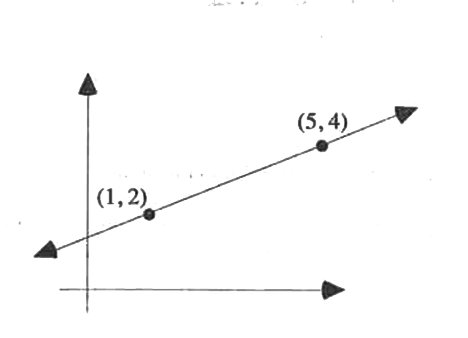 A1/4B1C1/2D3/2
A1/4B1C1/2D3/2 - Question 2 - Select One
What is the slope of the line containing the points (-2,7) and (3, -3) ?
A0.04B14C0D−2
Find the slope of a line perpendicular to the line which passes through each pair of the following points (-k, h) and (b, -f)
View SolutionFind the slope of a line parallel to the which passes through each pair of the following points:
(0, 0) and (5, 6)View SolutionFind the slope of a line perpendicular to the line which passes through each pair of the following points:
(0, 8) and (-5, 2)View SolutionFind the slope of a line perpendicular to the line which passes through each pair of the following points: (1, -11) and (5, 2)
View SolutionWrite the negatin of each of the statement :
Two lines are parallel if and only if they have the same slope.View SolutionShow that the three points (5, 1), (1, -1) and (11, 4) lie on a straight line. Further find
the slope of the line.View Solution
