A ray of light travelling in air in inciden tat grazing angle (inciden angle =90∘) on a long rectangular slab of a tranparent medium of thicknesst=1.0m . The point of incidence is the origin A(0,0). The medium has a variable of refraction n(y) given by
n(y)=[ky3/2+1]1/2
wherek=1.0(m)−3/2
The refractive index of air is 1.0.
a. Obtain a relation between the slop of the trajectory of the ray at point B(x,y) in the medium and the incident angle at the point.
b. Obtain an equation for the trajectory y(x) of the ray in the medium.
c. Determing the coordinates (x1,y1) of point P, where the ray intersects the upper surface of the slab-air boundary.
d. Indicate the path of the ray subsequently.
![A ray of light travelling in air in inciden tat grazing angle (inciden angle =90^@) on a long rectangular slab of a tranparent medium of thicknesst=1.0m . The point of incidence is the origin A(0,0) . The medium has a variable of refraction n(y) given by n(y)=[ky^(3//2)+1]^(1//2) wherek=1.0(m)^(-3//2) The refractive index of air is 1.0. a. Obtain a relation between the slop of the trajectory of the ray at point B(x,y) in the medium and the incident angle at the point. b. Obtain an equation for the trajectory y(x) of the ray in the medium. c. Determing the coordinates (x(1),y(1) ) of point P, where the ray intersects the upper surface of the slab-air boundary. d. Indicate the path of the ray subsequently.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V04_C01_S01_117_Q01.png)
m=y34 (b) 4y14=x (c) (4, 1)
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - EXAMPLE
75 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - EXERCISE
45 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assignment (Section - I) Subjective Type Questions
6 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment SECTION - D (Assertion & reason type Question)
10 Videos
Similar Questions
A ray of light travelling in air is incident at grazing angle (incident angle=90∘) on a long rectangular slab of a transparent medium of thickness t=1.0 (see figure). The point of incidence is the origin A(O,O) .The medium has a variable index of refraction n(y) given by :n(y)=[ky3/2+1]1/2 ,where k=1.0m−3/2.the refractive index of air is 1.0<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/NG_PHY_RO_C01_E01_029_Q01.pngwh=80%mx-autosty≤=background:white;><br>(i)Obta∈arelationbetweentheslopeofthetrajec→ryoftherayatap∮B(x,y)∈themediumandthe∈cnt∠attˆp∮<br>(ii)obta∈anequationforthetrajec→ryy(x)oftheray∈themedium.<br>(ii)Determinethec∞rd∈ates(x_(1),y_(1))ofthep∮P.where the ray the ray intersects upper surface of the slab -air boundary.
Indicate the path of the ray subsequently.
View SolutionA light ray enters from medium A to medium B as shown in the figure. The refractive index of medium B relative to A will be
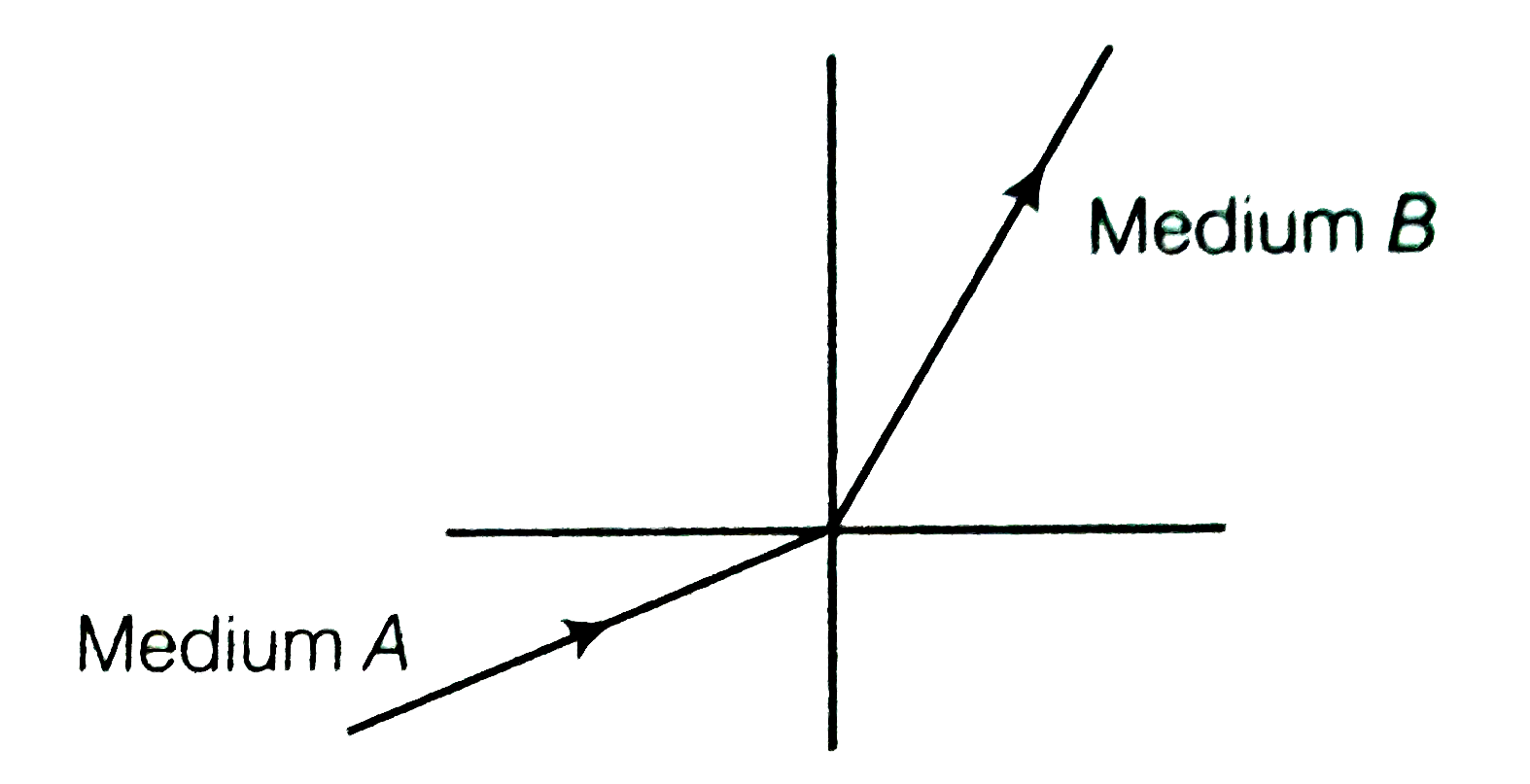
View SolutionA ray of ordinary light is travelling in air. It is incident on air glass pair at a polarising angle of 56∘. Find the angle of refraction in glass.
View SolutionA ray of light travelling in air strikes the surface of glass at angle of 450. The angle of refraction in the glass will be :
View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√(1+y) . If the thickness of the slab is d=2m, determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionA ray of light is incident perpendicularly on a glass slab. The angle of incidence is 900.
View SolutionA ray of light travelling in air is inciden at angle of inciden 30∘ on one surface of slab in which refractive index varies with y. The light travels along the curve y=4x2 ( y and x are in meter) in the slab. Find out the refractive index of the slab at y=1/2m in the slab.

View SolutionA ray of light travelling in air is incident at grazing incidence on a slab with variable refractive index, n (y)=[ky3/2+1]1/2 where k=1m−3/2 and follows path as shown in the figure. What is the total deviation produced by slab when the ray comes out.

View SolutionLight travelling in air falls at an incidence angle of 2∘ on one rafracting surface of a prism of refractive index 1.5 and angle of refraction 4∘. The medium on the other side is water (n=4/3) . Find the deviation produced by the prism.
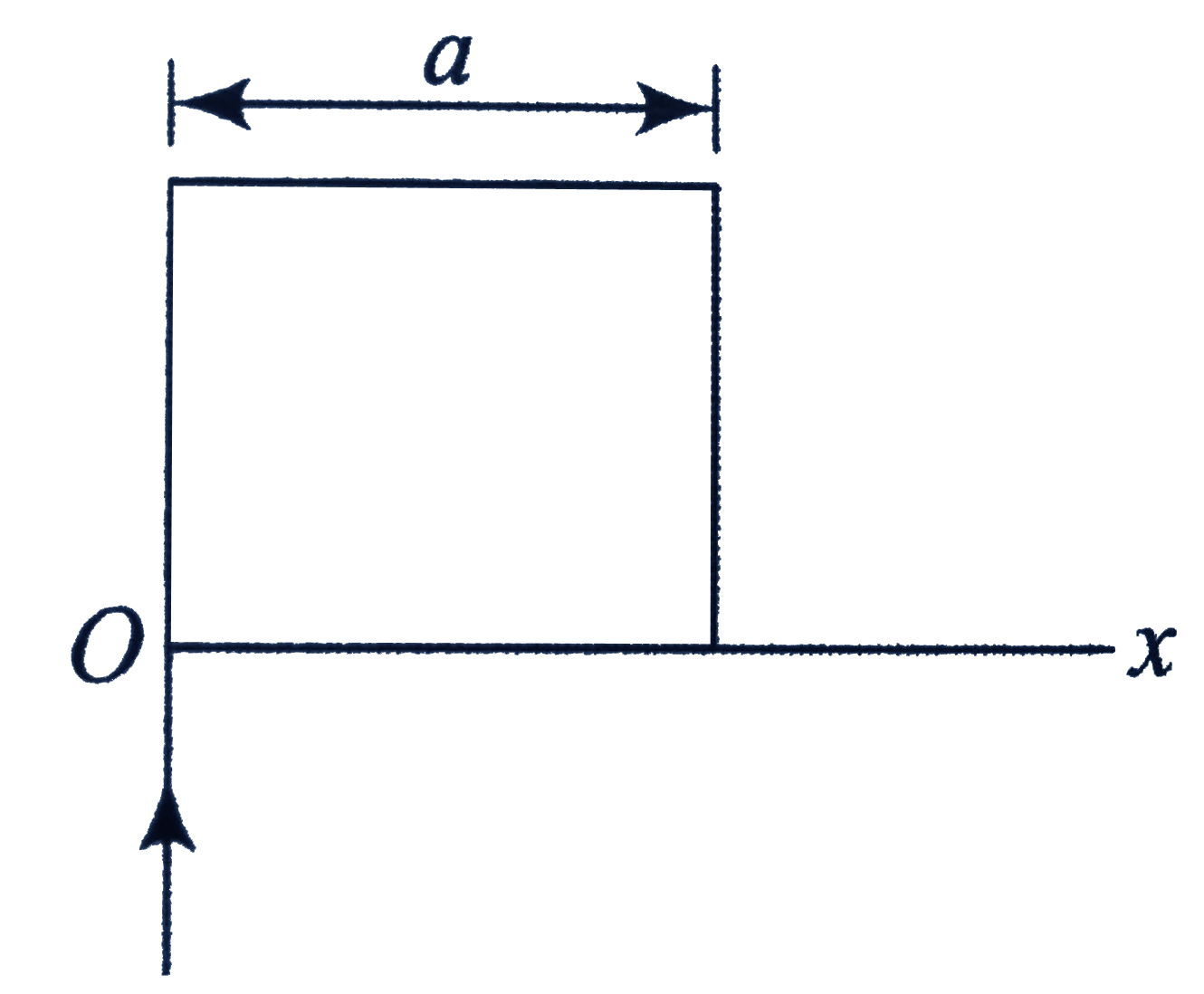
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
View Solution
