A spherical planet far out in space has a mass M0 and diameter D0. A particle of mass m falling freely near the surface of this planet will experience an accelertion due to gravity which is equal to
To find the acceleration due to gravity experienced by a particle of mass m falling freely near the surface of a spherical planet with mass M0 and diameter D0, we can follow these steps:
Step 1: Identify the relevant formula for gravitational force
The gravitational force F acting on the particle of mass m due to the planet can be expressed using Newton's law of gravitation:
F=GM0mR2
where G is the universal gravitational constant, M0 is the mass of the planet, m is the mass of the particle, and R is the radius of the planet.
Step 2: Relate the diameter to the radius
Given that the diameter of the planet is D0, we can find the radius R as:
R=D02
Step 3: Substitute the radius into the gravitational force formula
Substituting R=D02 into the gravitational force equation, we have:
F=GM0m(D02)2
This simplifies to:
F=GM0mD204=4GM0mD20
Step 4: Calculate the acceleration due to gravity
The acceleration due to gravity g at the surface of the planet is defined as the force per unit mass of the particle:
g=Fm
Substituting the expression for F we derived:
g=4GM0mD20m
The mass m cancels out:
g=4GM0D20
Final Result
Thus, the acceleration due to gravity near the surface of the planet is:
g=4GM0D20
The gravitational force F acting on the particle of mass m due to the planet can be expressed using Newton's law of gravitation:
F=GM0mR2
where G is the universal gravitational constant, M0 is the mass of the planet, m is the mass of the particle, and R is the radius of the planet.
Given that the diameter of the planet is D0, we can find the radius R as:
R=D02
Substituting R=D02 into the gravitational force equation, we have:
F=GM0m(D02)2
This simplifies to:
F=GM0mD204=4GM0mD20
The acceleration due to gravity g at the surface of the planet is defined as the force per unit mass of the particle:
g=Fm
Substituting the expression for F we derived:
g=4GM0mD20m
The mass m cancels out:
g=4GM0D20
Thus, the acceleration due to gravity near the surface of the planet is:
g=4GM0D20
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - Try Yourself
33 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -A (Objective Type Questions (one option is correct))
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
A spherical planet far out in space has mass 2M and radius a. A particle of mass m is falling freely near its surface. What will be the acceleration of that particle ?
View SolutionA planet has twice the mass of earth and of identical size. What will be the height above the surface of the planet where its acceleration due to gravity reduces by 36% of its value on its surface ?
View SolutionA thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then
View SolutionThe mass of a planet is twice the mass of earth and diameter of the planet is thrie the diameter of the earth, then the acceleration due to gravity on the planet's surface is
View SolutionA particle of mass M is at a distance a from surface of a thin spherical shell of equal mass and having radius a.
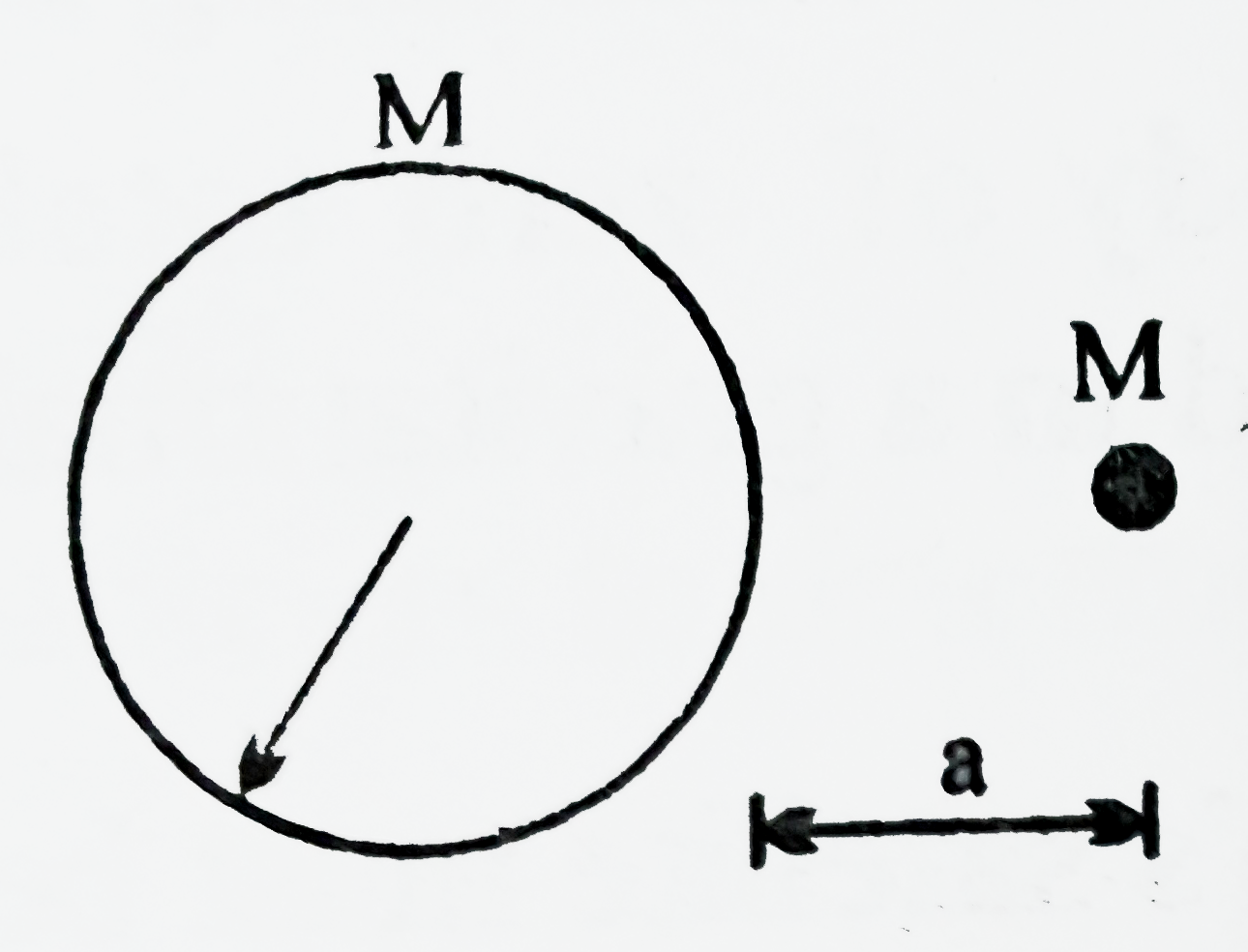
View SolutionA particle of mass M is at a distance a from surface of a thin spherical shell of equal mass and having radius a.
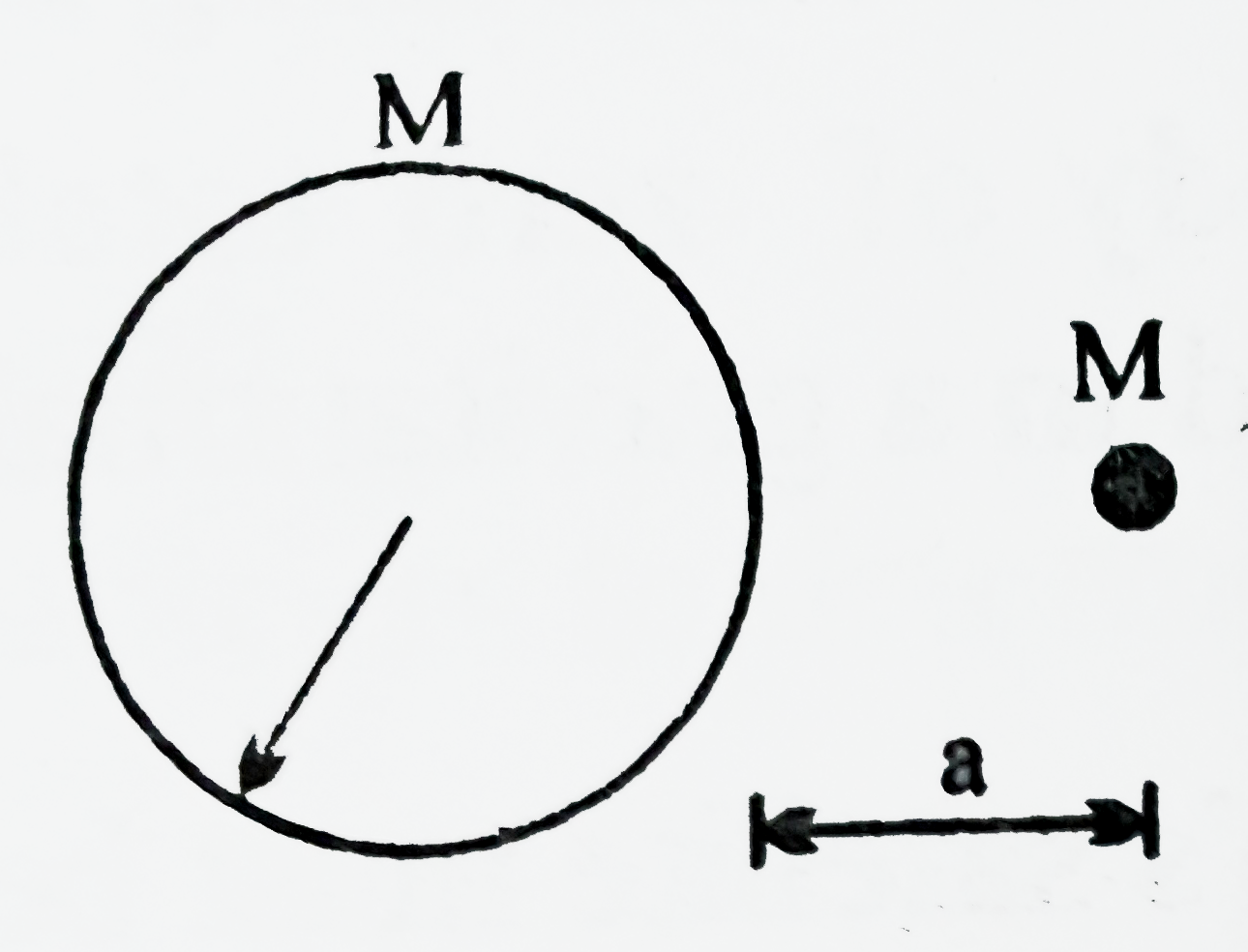
View SolutionThe mass and diameter of a planet have twice the value of the corresponding parameters of earth. Acceleration due to gravity on the surface of the planet is
View Solution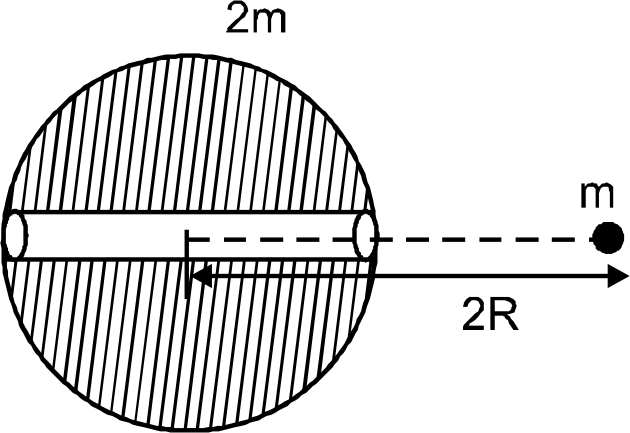
A solid spherical planet of mass 2m and radius 'R' has a very small tunnel along its diameter. A small cosmic particle of mass m is at a distance 2R from the centre of the planet as shown. Both are initially at rest, and due to gravitational attraction, both start moving toward each other. After some time, the cosmic particle passes through the centre of the planet. (Assume the planet and the cosmic particle are isolated from other planets)
View SolutionA planet has mass equal to mass of the earth but radius one fourth of radius of the earth . Then escape velocity at the surface of this planet will be
View SolutionIf a planet consists of a satellite whose mass and radius were both half that of the earh, then acceleration due to gravity at its surface would be
View Solution
