A cell of e.m.f. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F. isSolution in Bengali
1n
1n+1
nn+1
n+1n
The correct Answer is:C
Step by step video, text & image solution for A cell of e.m.f. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F. is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The e.m.f and internal resistance of two cells are varepsilon_(1),varepsilon_(2) and r_(1) and r_(1) respectively,are connected in series with an external resistance R . Derive an expression for equivalent e.m.f and internal resistance.
View SolutionTwo cells with same e.m.f. 'E' and different internal resistances r andr, are connected in series to an external resistance 'R'. The value of R so that the p.d. across the first cell be zero is
View SolutionSeven identical cells each of e.m.f. E and internal resistance r are connected as shown . The potential difference between A and B is
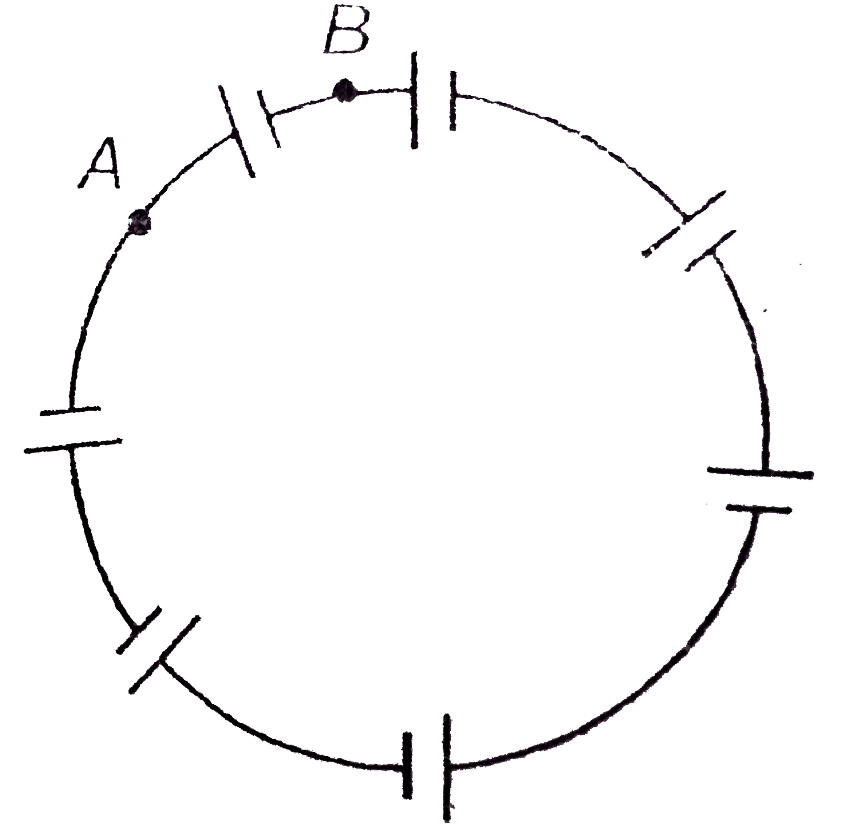
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View SolutionA cell of emf E is connected across a resistance R. The potential difference between the terminals of the cell is found to be V. The internal resistance of the cell must be -
View SolutionA cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View SolutionA cell of e.m.f . 2 V and internal resistance 0.1Ω is connected to a 3.9Ω external resistance . What will be the potential difference across the terminal of the cell ?
View SolutionTwo cells, of e.m.f. 2E and E, and internal resistance 2 r and r respectivley are connected in parallel. Obtain the expression for the equivalent e.m.f and the internal resistance of the combination?
View Solution
