
Two blocks A (1 kg) and B (2 kg) are connected by a string passing over a smooth pulley as shown in the figure. B rests on rough horizontal surface and A rest on B. The coefficient of friction between A and B is the same as that between B and the horizontal surface. The minimum horizontal force F required to move A to the left is 25 N. The coefficient of friction is:
0.67
0.5
0.4
0.25
The correct Answer is:B
Let f1 be the magnitude of limiting frictional force between the blocks and f2 be the magnitude of limiting frictional forcfe between the blocks and horizontal surface. The free body diagrams for both the blocks is as shown . Applying Newton's second low to both the blocks
F−f1−T=mAa (1)
F−f1−f2=mBa (2)
For F to just pull the blocks, acceleration of blocks a=0.
Therefore from equation (1) and (2) ,
F=2f1+f2 or 25=μ(2×1×10+2×10) solving we get μ=0.5
Similar Questions
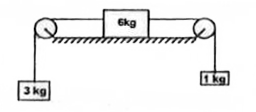
Three blocks of masses 3 kg, 6 kg and 1 kg are connected by a string passing over two smooth pulleys attached at the two ends of the horizontal surface. If the co-efficient of friction between the block and the surface is 0.6, the frictional force acting on the block of mass 6 kg is
View SolutionTwo blocks A & B are connected by a light inextensible string passing over a fixed smooth pulley as shown in the figure. The coefficient of friction between the block A and the horizontal table is μ=0.2. If the block A is just to slip, find the ratio of the masses of the blocks.
View SolutionA block A of mass 2kg rests on another block B of mass 8kg which rests on a horizontal floor. The coefficient of friction between A and B is 0.2 while that between B and floor is 0.5.When a horizontal floor F of 25N is applied on the block B the force of friction between A and B is
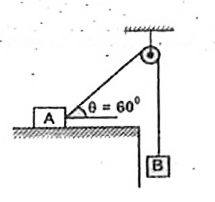
View SolutionTwo blocks A and B of respective masses 6 kg and 4 kg are connected with a string passing over a light friction less pulley as shown in the figure . The coefficient of friction between the block A and horizontal surface is 0.4 . Then the minimum mass of block C which should be placed over A to prevent it from moving is :
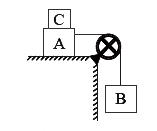
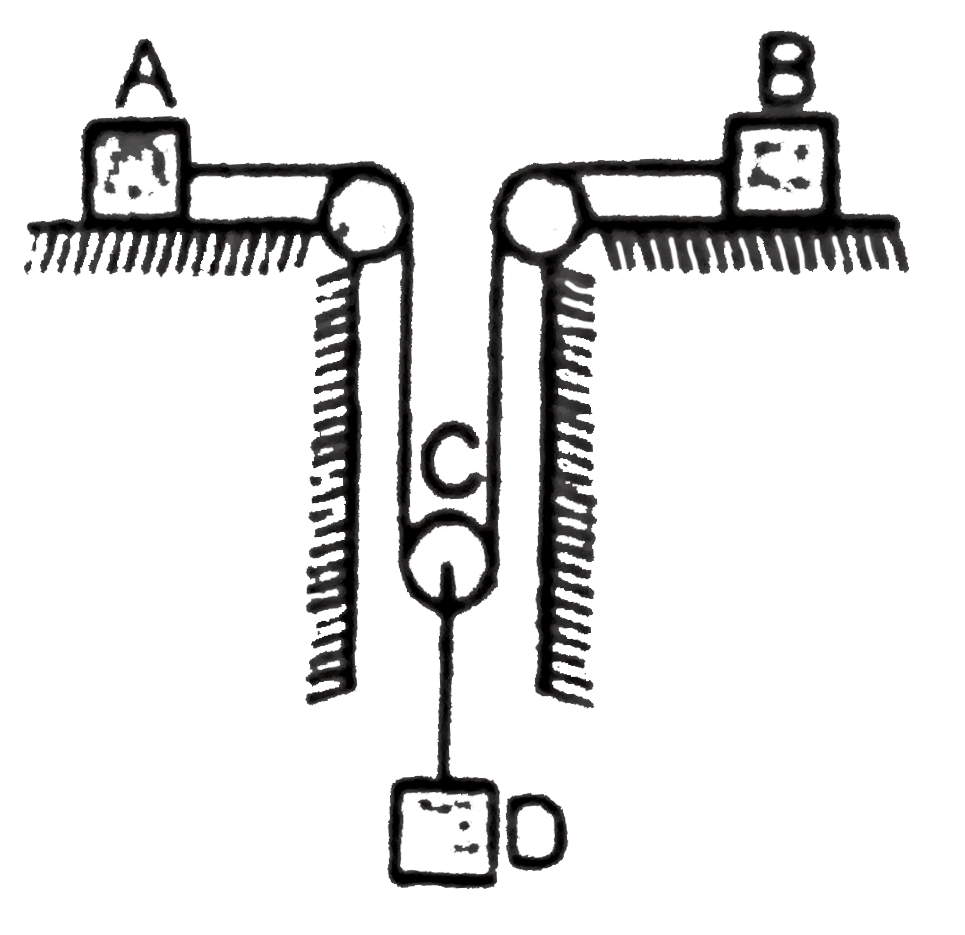
View SolutionBlocks A and B mass 5 kg and 3kg are connected by a light inextensible string passing under a smooth light pulley C which carries a particle D of mass 4 kg. A and B rest on a horizontal rough surfaces as shown in the diagram. The coefficient of friction is same for both A and B and is just sufficient to prevent A but not B, from moving. Find the coefficient of friction.
View SolutionBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then

Acceleration of upper block is
View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.
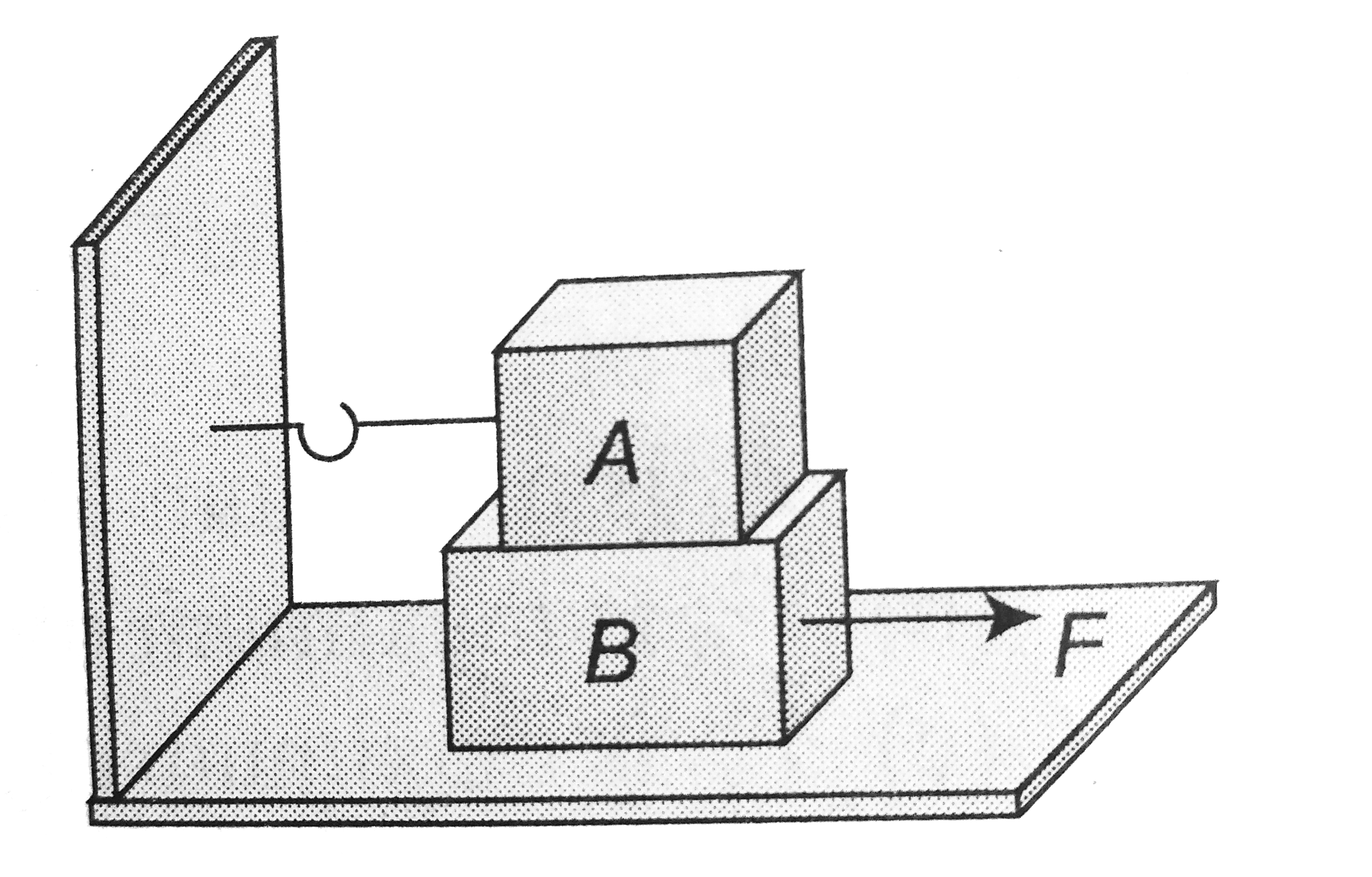
View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.

View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.

View SolutionTwo block A and B of masses 6kg and 3kg rest on a smooth horizontal surface as shown in figure If coefficient of friction between A and Bb is 0.4 the maximum horizontal force which can make them move without separation is

View Solution
