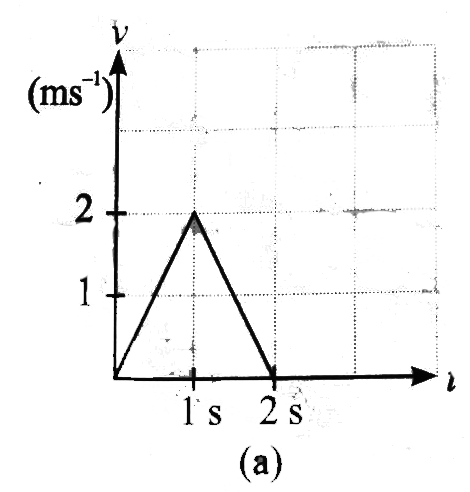

Figure shows (vx,t) and (vy,t) diagram for a body of unit mass. Find the force as a function of time.
Cosider figure (a)
vx=2t for 0<t<1s
=2(2−t) for 1<t<2s
=0 for t<2s
From figure (b)vy=t for 0<t<1s
=1 for t>1s
Fx=max=mdvxdt
=1×2=2N for 0<t<1s
=1(−2)=−2N for 1s<t<2s
=0 for t>2s
Fy=may=mdvydt
=1×1=1N for 0<t<1s
=0 for t>1s
Hence, F=Fxˆii+Fyˆj
=(2ˆi+ˆj)N for 0<t<1s
=−2ˆiN for 1s<t<2s
=0 for t>2s
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Multiple correct Answer Type
54 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type
22 Videos
Similar Questions
Knowledge Check
Figure shows (x,t) (y,t) diagram of a particle moving in 2-dimensions.
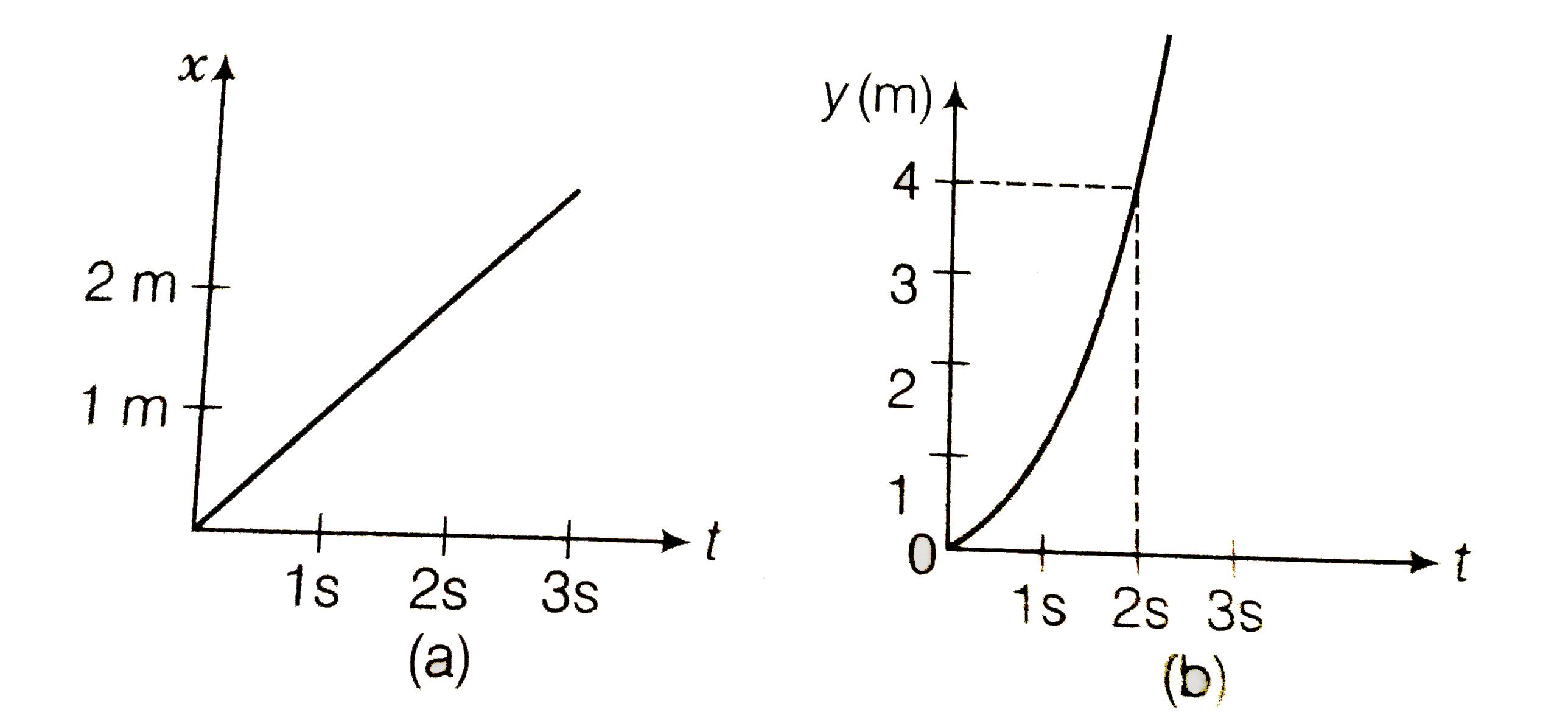
If the particle has a mass of 500 g , find the force (direction and magnitude) acting on the particle .A1N along y-axisB1N along x-axisC0.5N along x-axisD0.5N along y-axis
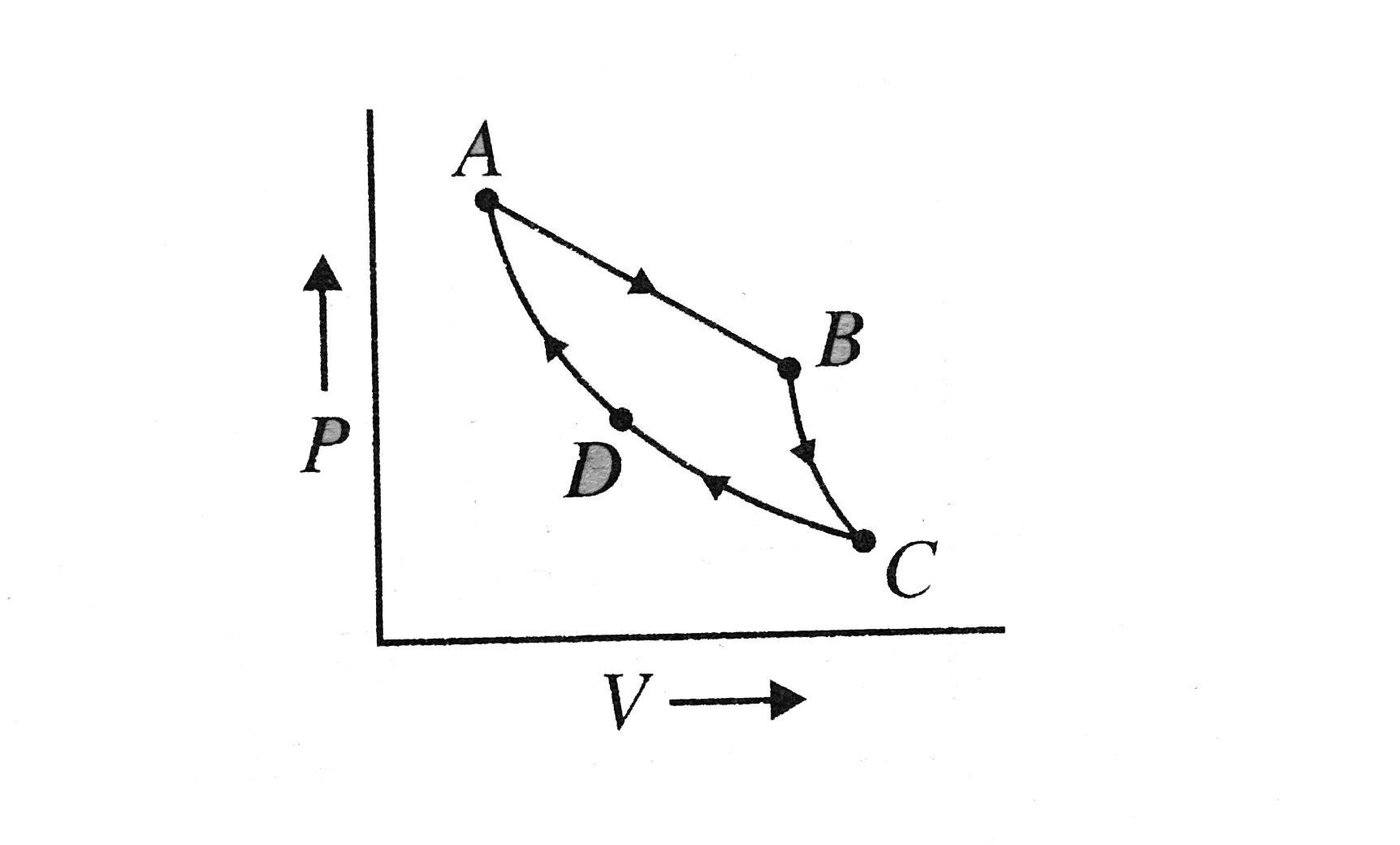
Figure. Shows the P−V diagram for a Carnot cycle. In this diagram
View SolutionWork done in time t on a body of mass m which is accelerated from rest to a speed v in time t1 as a function of time t is given by
View SolutionThe graph in figure shows the velocity v versus time t for a body. Which of the graphs shown in figure represents the correesponding acceleration versus time graphs ?
View SolutionA body of mass m is acceleratad uniformaly from rest to a speed v in a time T . The instanseous power delivered to the body as a function of time is given by
View Solution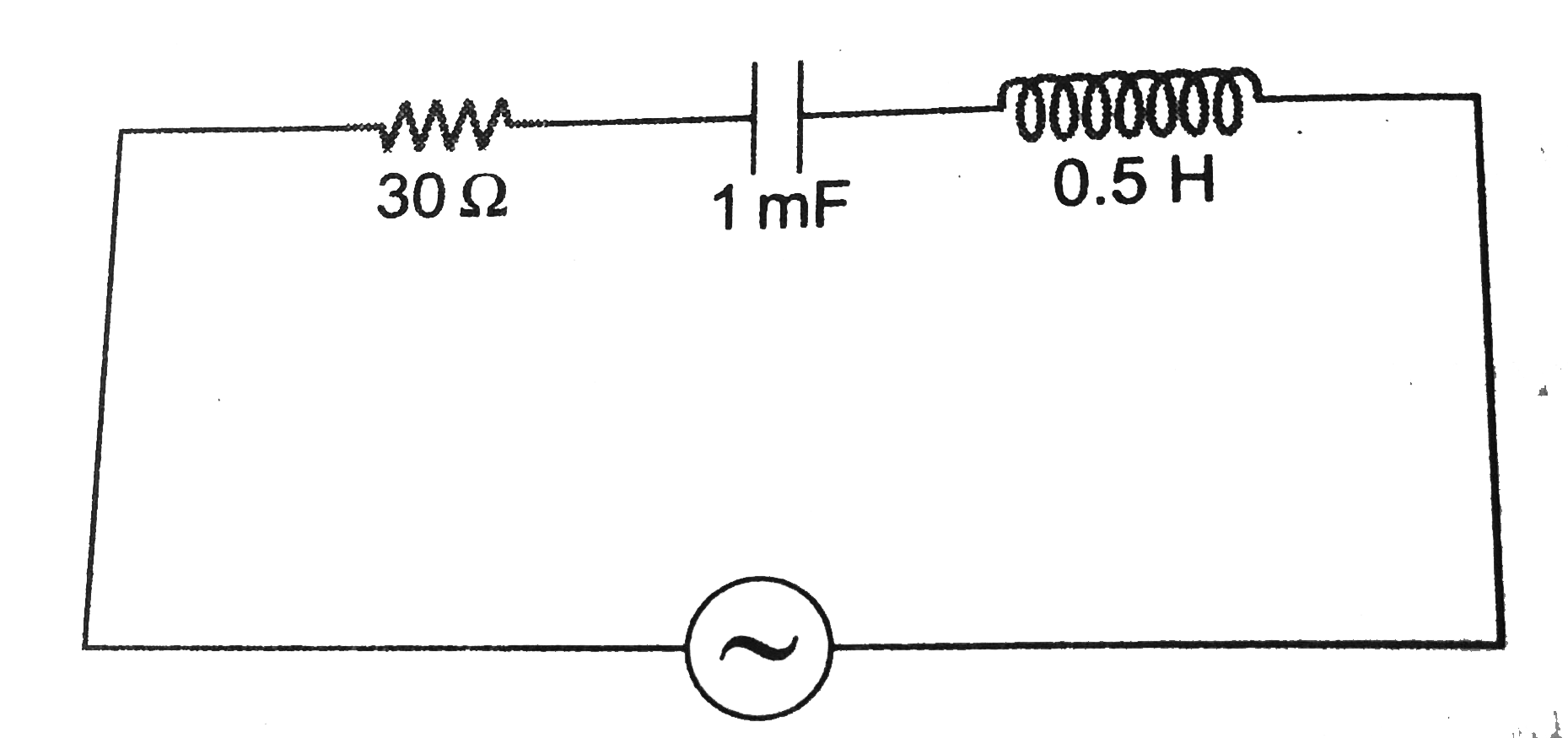
In the diagram shown in figure, V function is given. Find other four functions of time I,VC,VR and VL. Also, find power consumed in the circuit, V is given in volts and ω in rad/s.
View SolutionA body of mass m, accelerates uniformly from rest to V1 in time t1. The instantaneous power delivered to the body as a function of time t is.
View SolutionThe motion of a body is given by the equation dvdt=4−2v, where v is the speed in m/s and t in second. If the body was at rest at t = 0, then find
(i) The magnitude of initial acceleration
(ii) Speed of body as a function of time
View Solution