A simple harmonic plane wave propagatees along x-axis in a medium. The displacement of the particle as a function of time is shown in figure, for x=0(curve 1) and x=7 (curve 2)
The two particle are with a span of onewavelength.
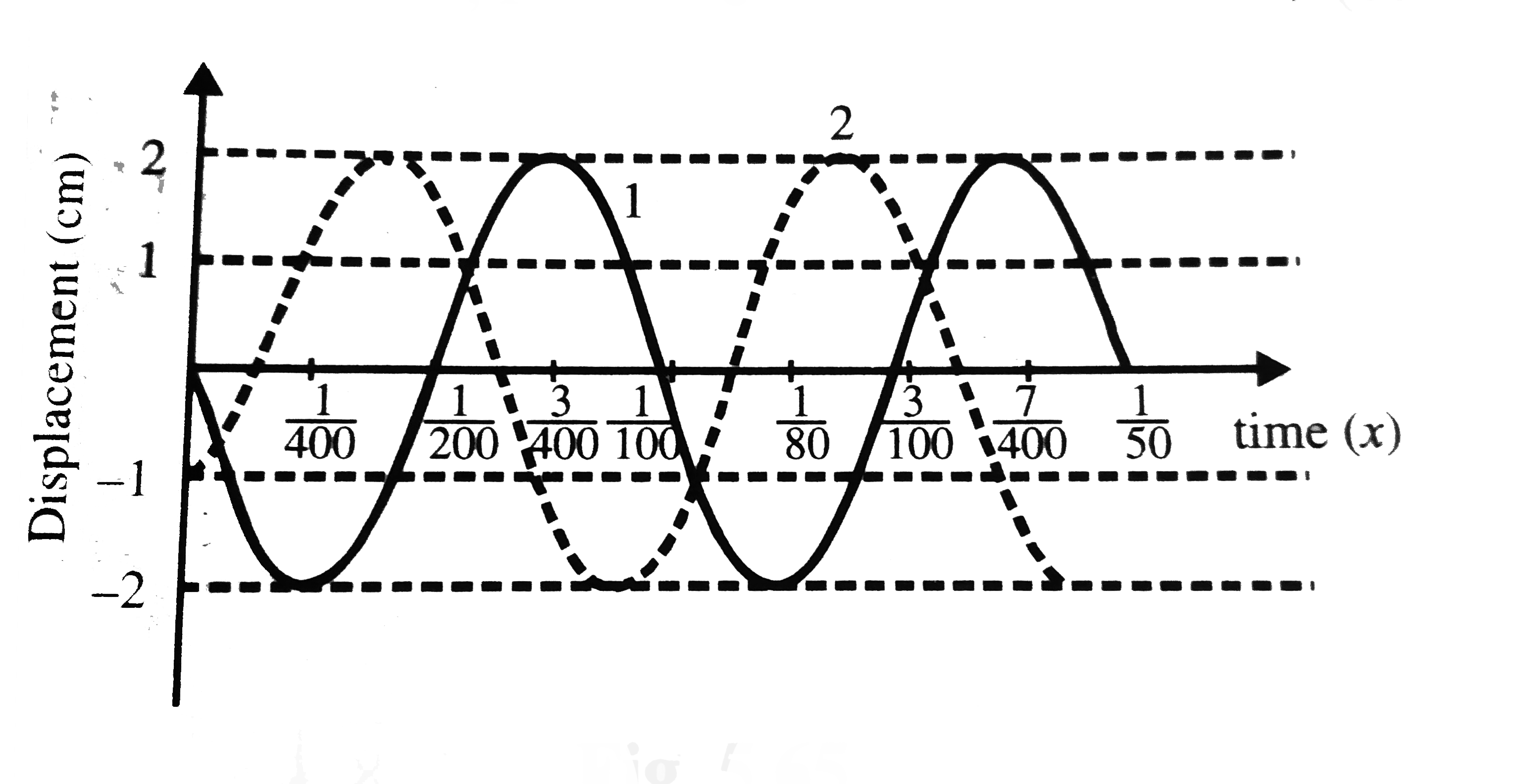
The speed of the wave is
12m/s
24m/s
8m/s
16m/s
The correct Answer is:a
Let general wave equation be y=Asin(ωt−kx+ϕ)
v=dydt=Aωcos(ωt−kx+ϕ)
For curve (1),x=0
at t=0,x=0, we have y=0
⇒0=Asin[ϕ]⇒sinϕ=0
⇒ϕ=0 or π
here ϕ=π (because velocity is negative) for curve (2),×=7cm
t=0,x=7cm,y=−1
−1=sin(−k×7+π)
⇒sin(−7k+π)=−1/2
⇒−7k+π=2nπ+7π6 or 2nπ+11π6
here ⇒−7k+π=2nπ+11π6
(because at t=0, velocity is positive)
⇒−7(2πλ)=2nπ+5π6
implieslammbda=(-14pi)/((5pi)/(6)+2npi)<br>
⇒λ=−8412n+5
for n=−1,λ=12cm
for n=−2,λ=8419cm (not possible)
because λ>7cm
v=fλ=100×12100=12m/s
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer9videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Assertion-Reasoning6videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct9videos
TRANSMISSION OF HEAT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
A simple harmonic plane wave propagatees along x-axis in a medium. The displacement of the particle as a function of time is shown in figure, for x=0(curve 1) and x=7 (curve 2)
The two particle are with a span of onewavelength.
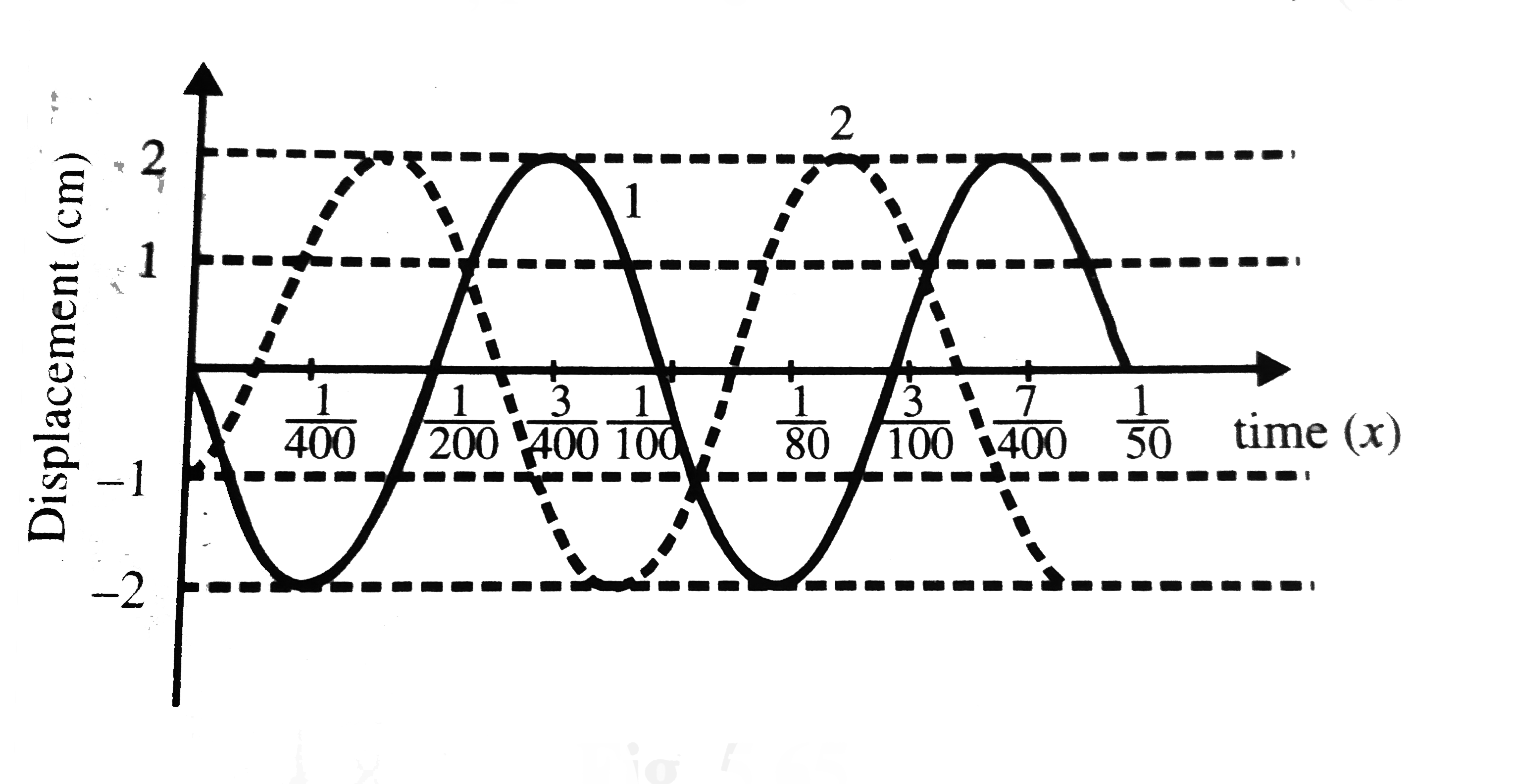
The wavelength of the wave isView SolutionA mechanical wave propagastes in a medium along the X-axis. The particles of the medium
View SolutionA transverse wave travels along x-axis . The particles of medium move
View SolutionFigure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region
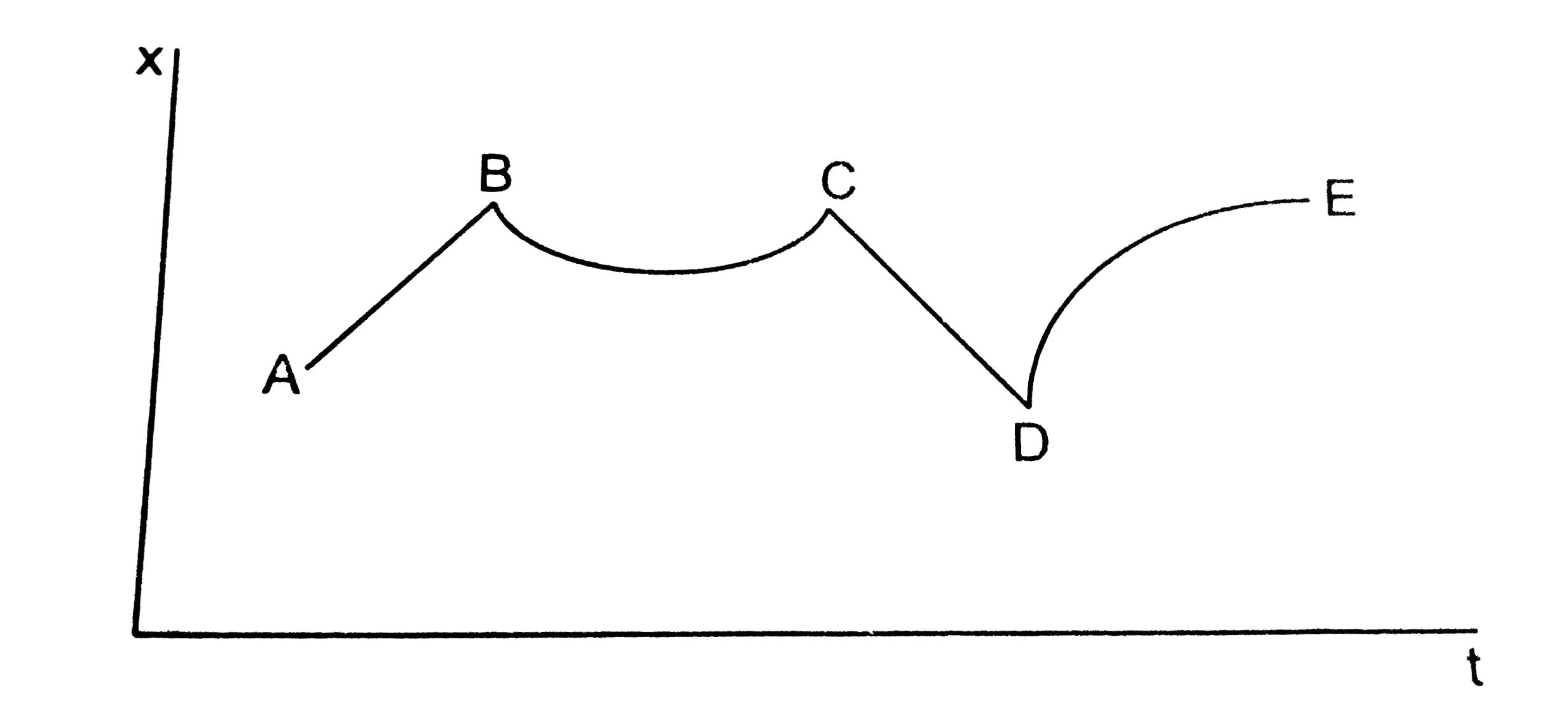 View Solution
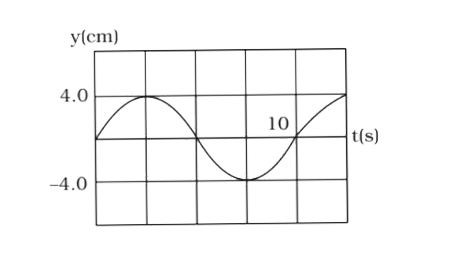
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
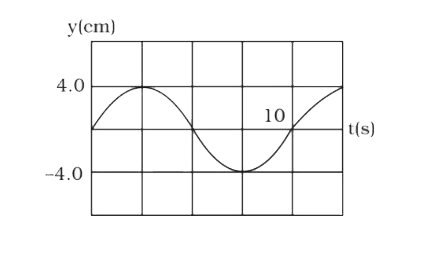
Q. The velocity of propagation of the wave is ?View SolutionSound waves are trqvelling along positive x - direction. Displacement of particle at any time t is as shows in figure. Select the correct statement.
 View Solution
View SolutionFigure shows the displacement time graph of a particle moving on the X-axis
 View Solution
View SolutionFigure shows the displacement-time graph of a particle moving on the X-axis
 View Solution
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. The transverse displacement of the string particle at as a function of time is shown in Figure.
The equation of the wave with all the constants evaluated is:
 View Solution
View SolutionA harmonic wave is travelling along +ve x-axis, on a stretched string. If wavelength of the wave gets doubled, then
View Solution
