A wave pulse starts propagating in the +x-direction along a non-uniform wire of length 10 m with mass per unit length given by μ=μ0+az and under a tension of 100 N. find the time taken by a pulse to travel from the lighter end (x=0) to the heavier end. (mu_(0)=10^(2) kg//m and a=9xx10^(-3)kg//m^(2)).
To solve the problem, we need to find the time taken by a wave pulse to travel from the lighter end of a non-uniform wire to the heavier end. The mass per unit length of the wire is given by μ=μ0+az, where μ0=102kg/m, a=9×10−3kg/m2, and the tension T=100N.
1. Identify the Speed of the Wave:
The speed of a transverse wave on a string is given by the formula:
v=√Tμ
where T is the tension and μ is the mass per unit length.
2. Substitute for Mass per Unit Length:
Since μ varies with z, we can write:
v=√100μ0+az=√100102+9×10−3z
3. Set Up the Differential Equation:
The relationship between distance z and time t can be expressed as:
v=dzdt
Therefore, we can write:
dz=vdt=√100μ0+azdt
4. Rearranging the Equation:
Rearranging gives us:
√μ0+azdz=10dt
5. Integrate Both Sides:
We need to integrate from z=0 to z=10 and from t=0 to t=T:
∫100√μ0+azdz=10∫T0dt
This simplifies to:
∫100√102+9×10−3zdz=10T
6. Evaluate the Integral:
The integral can be evaluated using substitution or numerical methods. The result of the integral will be:
23a(μ0+10a)3/2−(μ0)3/2
where a=9×10−3 and μ0=102.
7. Plugging in Values:
Substitute μ0 and a:
10T=23×9×10−3(102+10×9×10−3)3/2−(102)3/2
8. Solve for T:
After evaluating the expression, we find:
T≈0.23seconds
Final Answer:
The time taken by the pulse to travel from the lighter end to the heavier end is approximately T≈0.23seconds.
The speed of a transverse wave on a string is given by the formula:
v=√Tμ
where T is the tension and μ is the mass per unit length.
Since μ varies with z, we can write:
v=√100μ0+az=√100102+9×10−3z
The relationship between distance z and time t can be expressed as:
v=dzdt
Therefore, we can write:
dz=vdt=√100μ0+azdt
Rearranging gives us:
√μ0+azdz=10dt
We need to integrate from z=0 to z=10 and from t=0 to t=T:
∫100√μ0+azdz=10∫T0dt
This simplifies to:
∫100√102+9×10−3zdz=10T
The integral can be evaluated using substitution or numerical methods. The result of the integral will be:
23a(μ0+10a)3/2−(μ0)3/2
where a=9×10−3 and μ0=102.
Substitute μ0 and a:
10T=23×9×10−3(102+10×9×10−3)3/2−(102)3/2
After evaluating the expression, we find:
T≈0.23seconds
The time taken by the pulse to travel from the lighter end to the heavier end is approximately T≈0.23seconds.
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.1
9 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.2
23 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A wave pulse starts propagating in the x direction along a non uniform wire of length 10m with mass per unit length is given byμ=μ0+ax and under a tension of 100N. The time taken by a pulse to travel from the lighter end to heavier end (μ0=10−2kg/m and a=9×10−3kg/m2) is
View SolutionA wave pulse starts propagating in the x direction along a non uniform wire of length 10m with mass per unit length is given by μ=μ0+ax and under a tension of 100N. The time taken by a pulse to travel from the lighter end to heavier end (μ0=10−2kg/m and a=9×10−3kg/m2) is
View SolutionThe mass of a 10 m long wire is 100 grams. If a tension of 100 N is applied, calculate the time taken by a transverse wave to travel from one end to the other end of the wire.
View SolutionA piano string having a mass per unit length equal to 5.00×103kg/m is under a tension of 1350N, Find the speed with which a wave travels on this string.
View SolutionA wire of length L is fixed at both ends such that F is tension in it. Its mass per unit length varies from one end to other end as μ=μ0x, where μ0 is constant. Find time taken by a transverse pulse to move from lighter end to its mid point.
View SolutionA way pulse is travelling on a string of linear mass density 6.4×10−3kgm−1 under a load of 80kgf. Calculate the time taken by the pulse to traverse the string, if its length is 0.7m.
View SolutionA non-uniform wire of length l and mass M has a variable linear mass density given by μ=kx, where x is distance from one end of wire and k is a constant. Find the time taken by a pulse starting at one end to reach the other end when the tension in the wire is T.
View SolutionTwo strings with linear mass densities μ1=0.1kg/m and μ2=0.3kg/m are joined seamlesly. They are under tension of 20N. A travelling wave of triangular shape is moving from lighter to heavier string.
View SolutionCalculate the velocity of a transverse wave along a string of length 2m and mass 0.06kg under a tension of 500N.
View SolutionThe figure represents two snaps of a travelling wave on a string of mass per unit length μ=0.25kg/m. The first snap is taken at t=0 and the second is taken at t=0.05s.
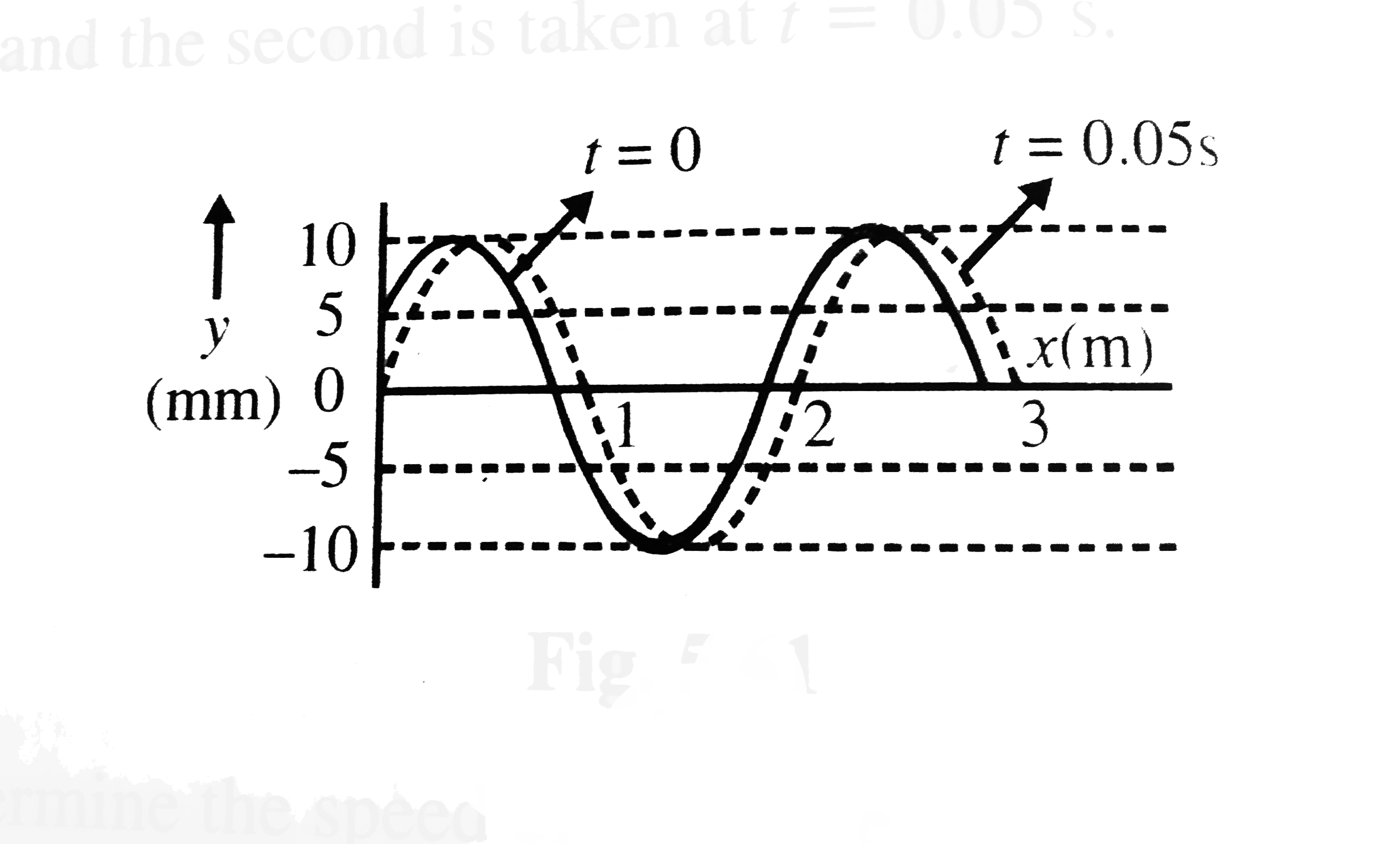
Determine the speed of the wave.
View Solution
