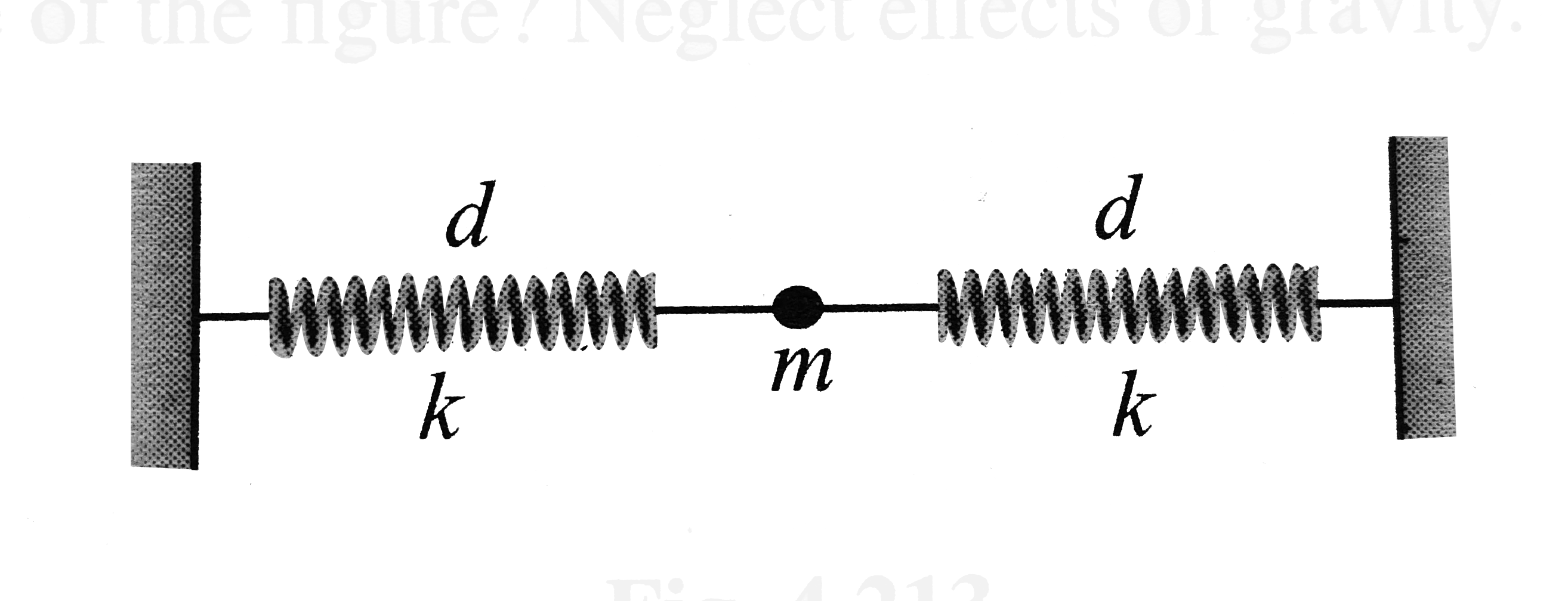
A small body of mass m is connected to two horizontal spring of elastic constant k, natural length 3d4. In the equilibrium position botgh springs are stretched to length d, as shown in Fig. What will be the ratio of perod of the motion (TbTa) If the body is displaced horizontally by a small distance where Ta is the time period when the particle owscillates along the line of spring Tb is time plane of the figure? Neglect effect of gravity.
Initial stretch in both springs =d−3d4=d4
frestering=k(d(4)x)−k(d4−x)=2kx
⇒Ta=2π√mk
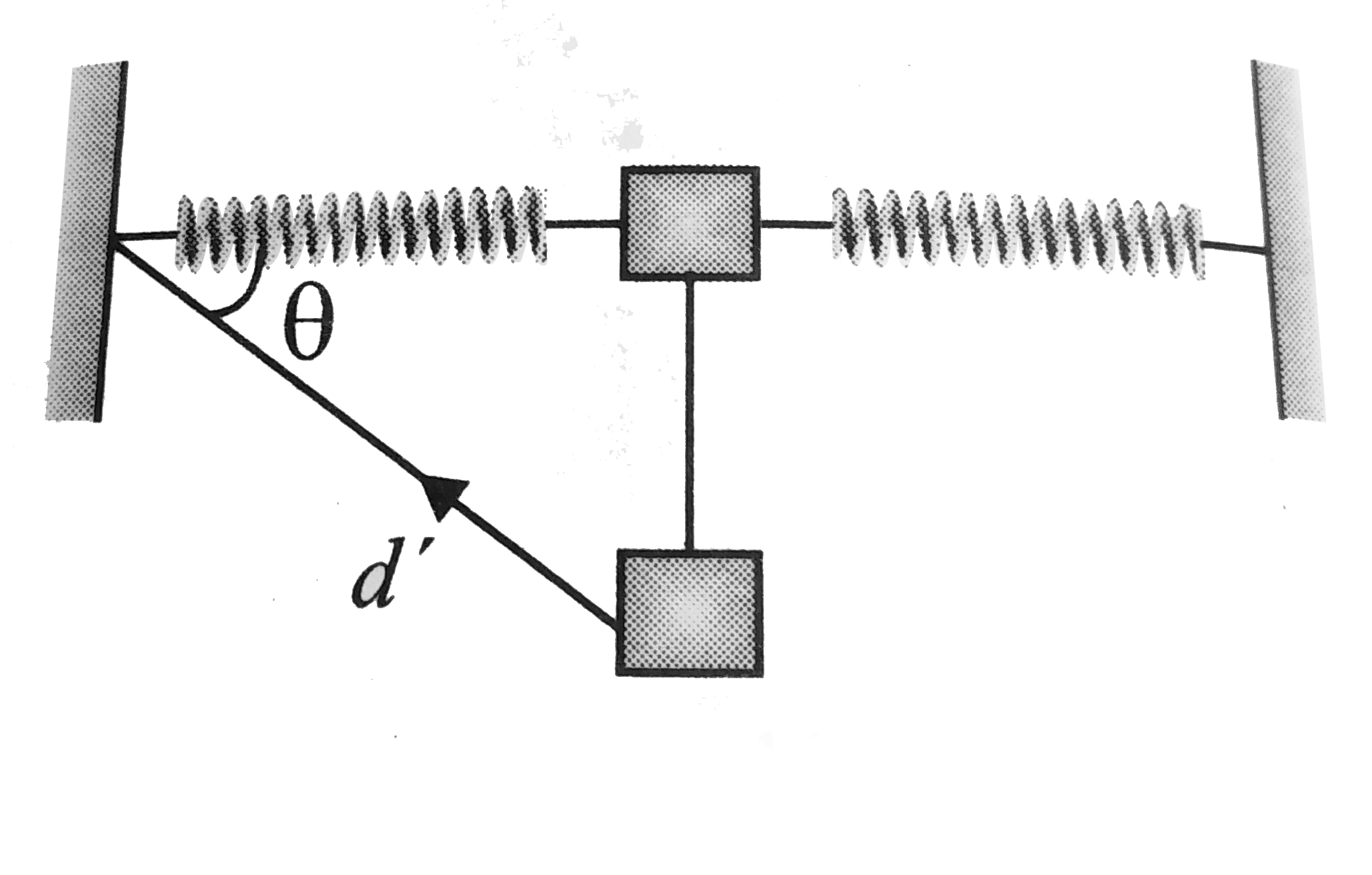
d'=dsecθ
x'=dsecθ−3d4=d(1cosθ−34)
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct Answer Type
29 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Comprehension
33 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution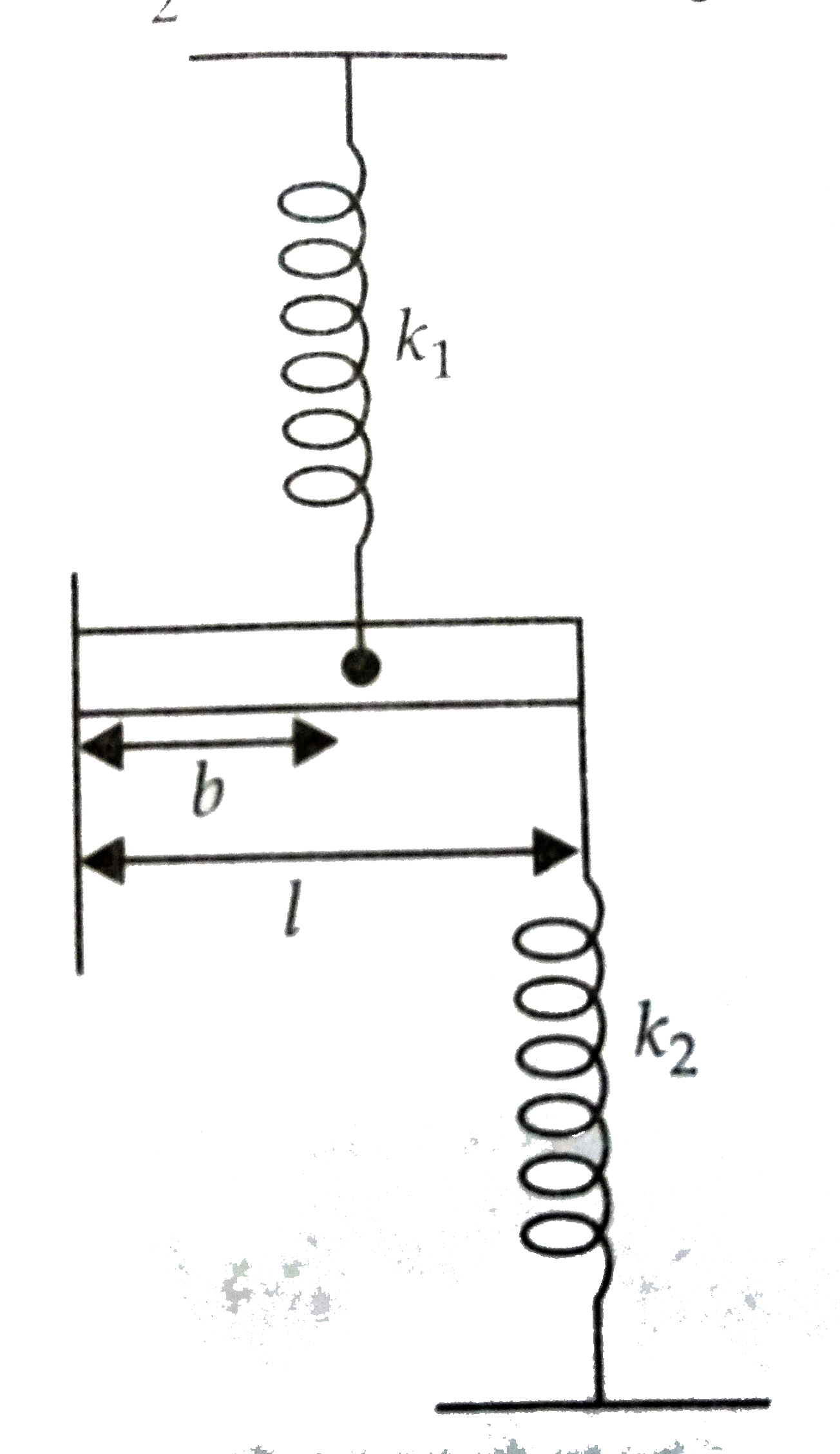
A rod of mass m and length l is connected by two spring of spring constants k1andk2, so that it is horizontal at equilibrium. What is the natural frequency of the system?
View Solution
Knowledge Check
A body of mass 20 g connected to a spring of spring constant k, executes simple harmonic motion with a frequency of (5/π) Hz. The value of spring constant is
A4Nm−1B3Nm−1C2Nm−1D5Nm−1
The frequency of oscillations of a mass m connected horizontally by a spring of spring constant k is 4 HZ. When the spring is replaced by two identical spring as shown in figure. Then the effective frequency is

View SolutionA spring of force constant k extends by a length X on loading . If T is the tension in the spring then the energy stored in the spring is
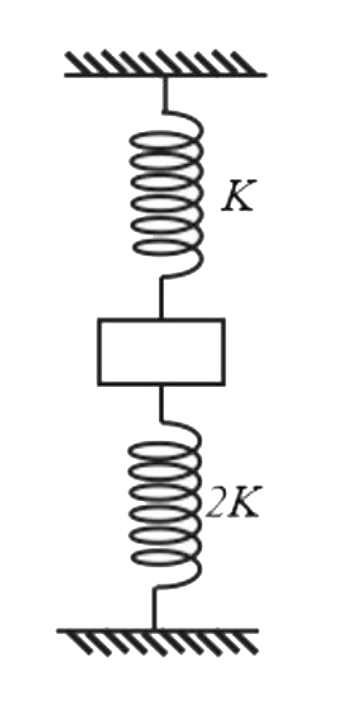
View SolutionA block of mass m is connected two springs of spring constant 2k annd k , respectively , as shown in the vertical plane. At equilibrium , both springs are compressed by same length. If suddenly lower spring is cut, then acceleration of block, just after spring cut , is
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionIn the figure, a block of mass m is rigidly attached to two identical springs of stiffness k each. The other ends of the springs are connected to the fixed wall. When the block is in equilibrium, length of each spring is b, which is greater than the natural length of the spring. The time period of the oscillation of the block if it is displaced by small distance perpendicular to the length of the springs and released. Space is gravity free.
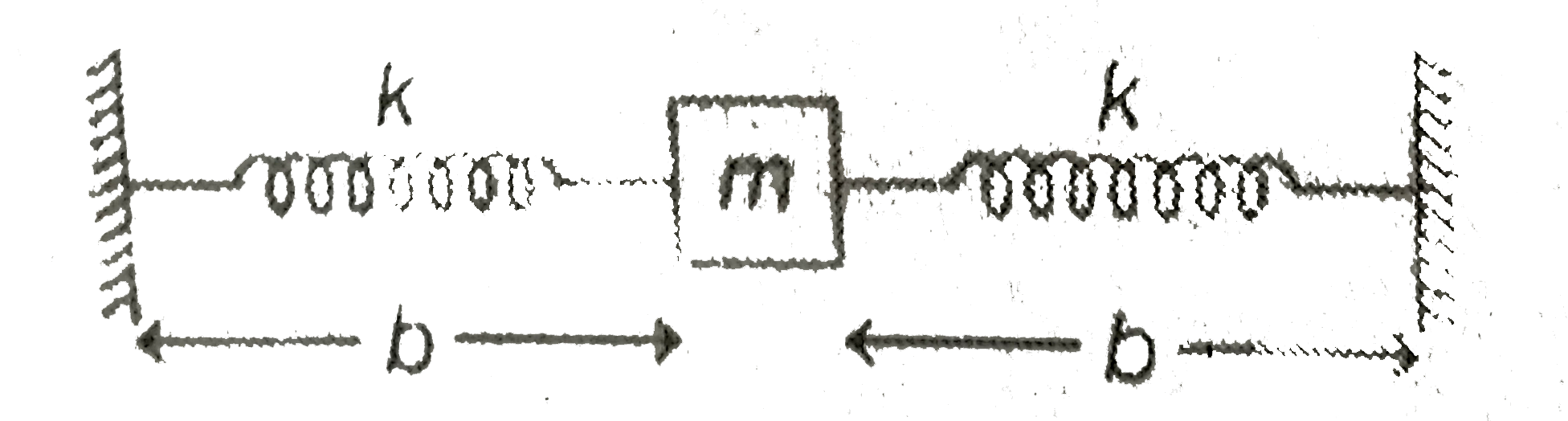
View SolutionA block of mass m lie on a horizontal smooth surface and connected with the springs at their natural length as shown in figure. When block slightly displaced then find the time period of oscillation.

View SolutionA horizontal metallic rod of mass 'm' and length 'l' is supported by two vertical identical springs of spring constant 'k' each and natral length l0 A current 'l' is flowing in the rod in the direction shown if the rod is in equilibrium then the length of each spring in this state is:
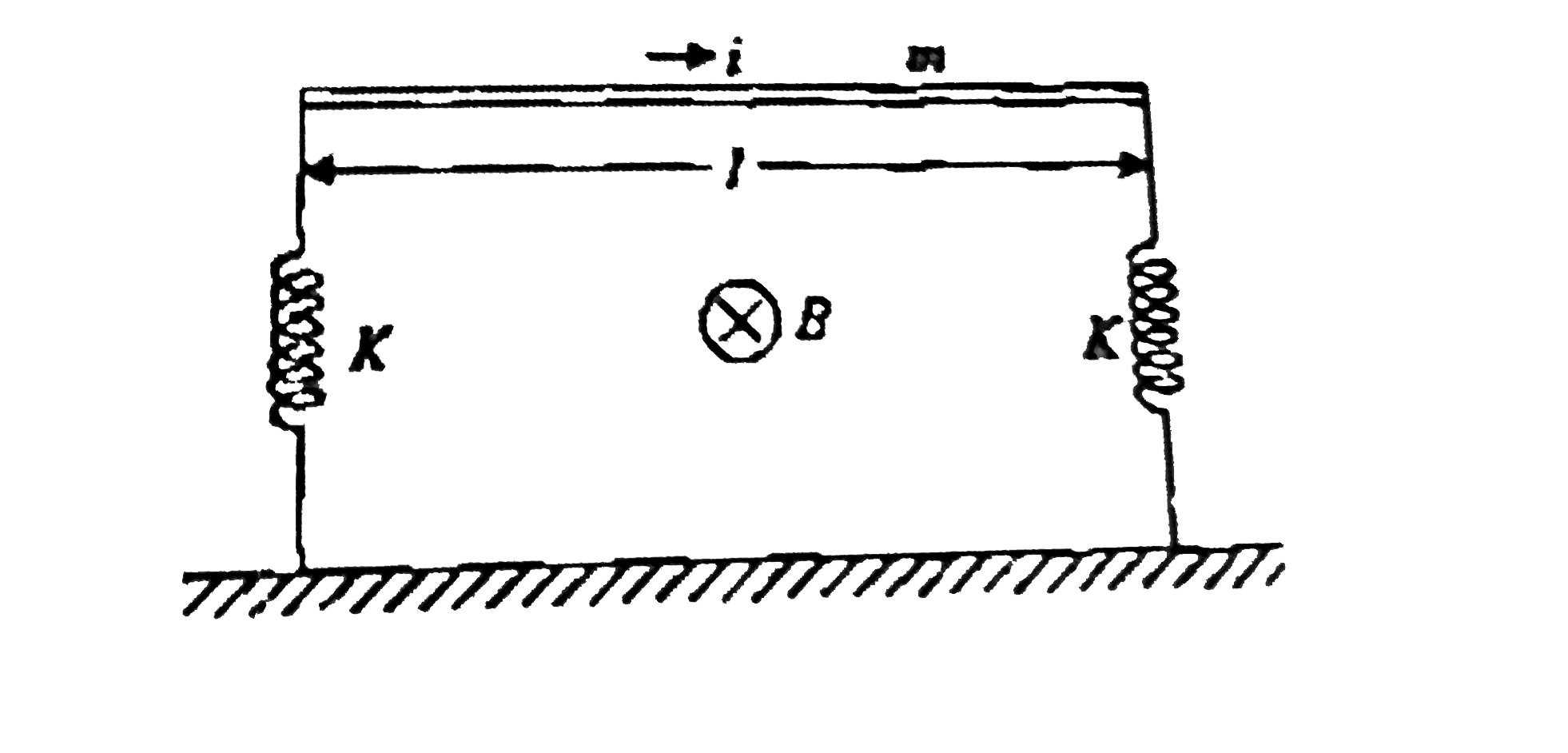
View Solution
