A gold rod of length l is accelerated in the horizontal direction with an accleration a0. The rod is held between two perfactly insulating clamps. Calculate the electric field set up in the rod. Take the mass of electron as m.
(a) E=ma0e
(b) E=ma0l
( c) zero
( d) none of these
The correct Answer is:A
To solve the problem of calculating the electric field set up in a gold rod of length l that is accelerated horizontally with an acceleration a0, we can follow these steps:
1. Identify the Forces Acting on the Rod:
The rod is being accelerated horizontally with an acceleration a0. According to Newton's second law, the force acting on the rod can be expressed as:
\(
F = m \cdot a_0
\)
where m is the mass of the rod.
2. Understand the Effect of Acceleration on Charges:
The acceleration of the rod causes the free electrons within the rod to experience a force. This force will cause a separation of charges, leading to the creation of an electric field within the rod.
3. Relate Electric Force to Electric Field:
The electric force acting on an electron due to the electric field E can be expressed as:
\(
F_e = e \cdot E
\)
where e is the charge of an electron.
4. Set Up the Equation:
Since the rod is accelerating, the force due to the acceleration must equal the electric force acting on the electrons. Therefore, we can equate the two forces:
\(
m \cdot a_0 = e \cdot E
\)
5. Solve for the Electric Field E:
Rearranging the equation to solve for the electric field E, we get:
\(
E = \frac{m \cdot a_0}{e}
\)
Final Expression:
Thus, the electric field set up in the rod is given by:
\(
E = \frac{m \cdot a_0}{e}
\)
The rod is being accelerated horizontally with an acceleration a0. According to Newton's second law, the force acting on the rod can be expressed as:
\(
F = m \cdot a_0
\)
where m is the mass of the rod.
The acceleration of the rod causes the free electrons within the rod to experience a force. This force will cause a separation of charges, leading to the creation of an electric field within the rod.
The electric force acting on an electron due to the electric field E can be expressed as:
\(
F_e = e \cdot E
\)
where e is the charge of an electron.
Since the rod is accelerating, the force due to the acceleration must equal the electric force acting on the electrons. Therefore, we can equate the two forces:
\(
m \cdot a_0 = e \cdot E
\)
Rearranging the equation to solve for the electric field E, we get:
\(
E = \frac{m \cdot a_0}{e}
\)
Thus, the electric field set up in the rod is given by:
\(
E = \frac{m \cdot a_0}{e}
\)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective
13 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
View Solution
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
View SolutionA thin uniform rod AB of mass m and length L is placed on a smooth horizontal table. A constant horizontal force of magnitude F starts acting on the rod at one of the ends AB, Initially, the force is perpendicular to the length of the rod. Taking the moment at which force starts acting as t=0, find.
(a) Distance moved by centre of mass of the rod in time t0.
(b) Magnitude of initial acceleration of the end A of the rod.
View SolutionA conducting wire of length l is placed on a rough horizontal surface, where a uniform horizontal magnetic field B perpendicular to the length of the wire exists. Least values of the forces required to move the rod when a current I is established in the rod are observed to be F1 and F2(<F1) for the two possible directions of the current through the rod, respectively. Find the weight of the rod and the coefficient of friction between the rod and the surface.
View SolutionOne fourth length of a uniform rod of length 2l and mass m is place don a horizontal table and the rod is held horizontal. The rod is released from rest. Find the normal reaction on the rod as soon as the rod is released.
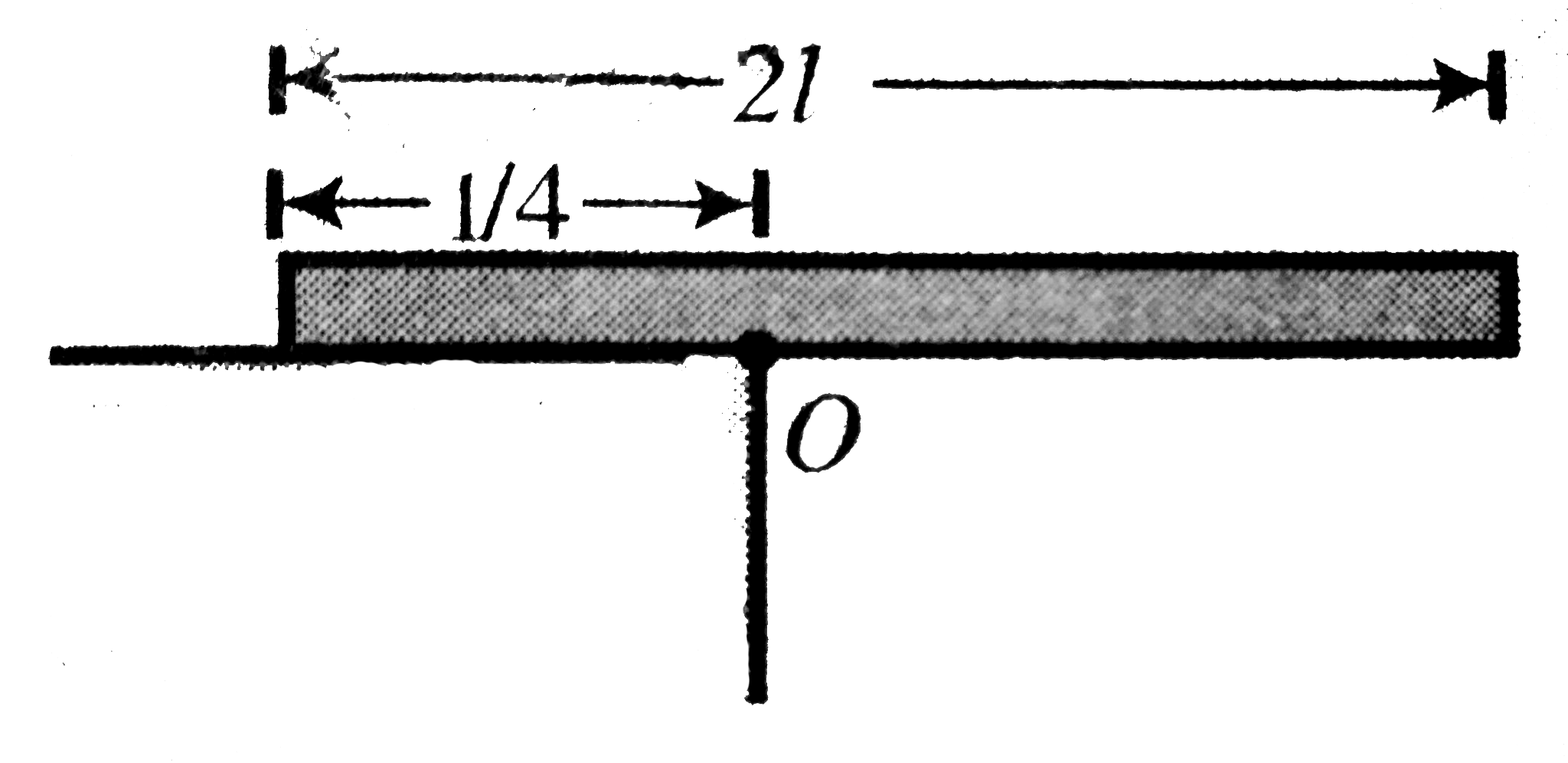
View SolutionA uniform rod of mass m and length l rests on a smooth horizontal surface. One of the ends of the rod is struck in a horizontal direction at right angles to the rod. As a result the rod obtains velocity v0. Find the force with which one-half of the rod will act ont he other in the process of motion.
View SolutionOne end of a uniform rod of mas m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity ω. The force exerted by the clamp on the rod has a horizontal component
View Solution
A uniform rod of length 4l and mass m is free to rotate about a horizontal axis passing through a point distant l from its one end. When the rod is horizontal its angular velocity is ω as shown in figure. calculate
(a). reaction of axis at this instant,
(b). Acceleration of centre of mass of the rod at this instant.
(c). reaction of axis and acceleration of centre mass of the rod when rod becomes vertical for the first time.
(d). minimum value of ω, so that centre of rod can complete circular motion.
View SolutionA thin homogeneous rod of mass m and length l is free to rotate in vertical plane about a horizontal axle pivoted at one end of the rod. A small ballof mass m and charge q is attached to the opposite end of this rod. The whole system is positioned in a horizontal electric field of magnitude E=mg2q. The rod is released from, shown position from rest.

What is the angular acceleration of the rod at the instant of releasing the rod?
View SolutionA uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View Solution
