Calculate the magnetic field at point O for the current-carrying wire segment shown in Fig. The wire consists of two straight portions and a circular arc of radius a, which subtends an angle θ.
To calculate the magnetic field at point O for the current-carrying wire segment consisting of two straight portions and a circular arc, we can follow these steps:
1. Identify the Components of the Wire:
The wire consists of two straight segments (AA' and CC') and a circular arc (AC) of radius a that subtends an angle θ.
2. Determine the Contribution from Straight Segments:
The magnetic field at point O due to the straight wire segments AA' and CC' can be analyzed. Since the current in both segments flows along the line towards point O, the contributions from these segments will cancel out due to symmetry. Therefore, the net magnetic field contribution from the straight segments is:
BAA′+BCC′=0
3. Focus on the Circular Arc:
The only contribution to the magnetic field at point O comes from the circular arc AC. We will calculate the magnetic field due to an elementary segment ds of the arc.
4. Magnetic Field Due to an Elementary Segment:
The magnetic field dB at point O due to an elementary segment ds of the arc can be expressed using the Biot-Savart law:
dB=μ04πIdsr2^r
Here, r is the distance from the segment to point O, which is equal to the radius a of the arc. Thus, we can write:
dB=μ04πIdsa2
5. Integrate Over the Arc:
To find the total magnetic field B at point O due to the entire arc, we need to integrate dB over the length of the arc. The length of the arc is given by aθ, where θ is in radians. Therefore:
B=∫dB=∫μ04πIdsa2
Since ds integrates to the length of the arc aθ:
B=μ04πIa2⋅(aθ)
6. Simplify the Expression:
Simplifying the expression gives:
B=μ0Iθ4πa
Final Result:
Thus, the magnetic field at point O due to the current-carrying wire segment is:
B=μ0Iθ4πa
The wire consists of two straight segments (AA' and CC') and a circular arc (AC) of radius a that subtends an angle θ.
The magnetic field at point O due to the straight wire segments AA' and CC' can be analyzed. Since the current in both segments flows along the line towards point O, the contributions from these segments will cancel out due to symmetry. Therefore, the net magnetic field contribution from the straight segments is:
BAA′+BCC′=0
The only contribution to the magnetic field at point O comes from the circular arc AC. We will calculate the magnetic field due to an elementary segment ds of the arc.
The magnetic field dB at point O due to an elementary segment ds of the arc can be expressed using the Biot-Savart law:
dB=μ04πIdsr2^r
Here, r is the distance from the segment to point O, which is equal to the radius a of the arc. Thus, we can write:
dB=μ04πIdsa2
To find the total magnetic field B at point O due to the entire arc, we need to integrate dB over the length of the arc. The length of the arc is given by aθ, where θ is in radians. Therefore:
B=∫dB=∫μ04πIdsa2
Since ds integrates to the length of the arc aθ:
B=μ04πIa2⋅(aθ)
Simplifying the expression gives:
B=μ0Iθ4πa
Thus, the magnetic field at point O due to the current-carrying wire segment is:
B=μ0Iθ4πa
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example
20 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.1
35 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
The resulting magnetic field at the point O due to the current carrying wire shown in the figure:
View SolutionThe magnetic field in a straight current carrying conductor wire is:
View SolutionFind the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure below

View SolutionCalculate the force on a current carrying wire in a uniform magnetic field as shown in Fig. 1.59.

View SolutionThe magnetic field at O due to current in the infinite wire forming a loop as a shown in Fig.

View SolutionA long current carrying wire is bent as shown. The magnetic field induction at O is

View SolutionThe strength of the magnetic field at a point r near a long straight current carrying wire is B. The field at a distance r2 will be
View SolutionThe strength of the magnetic field at a point r near a long straight current carrying wire is B. The field at a distance r2 will be
View SolutionB0 is the magnetic field at point P for a given straight wire as shown in figure. If this wirre is bent into a circular loop, then magnetic field at the centre of loop is
_PHY_E06_130_Q01.png)
View SolutionCalculate magnetic induction at point O if the wire carrying
a current I has the shape shown in Fig.
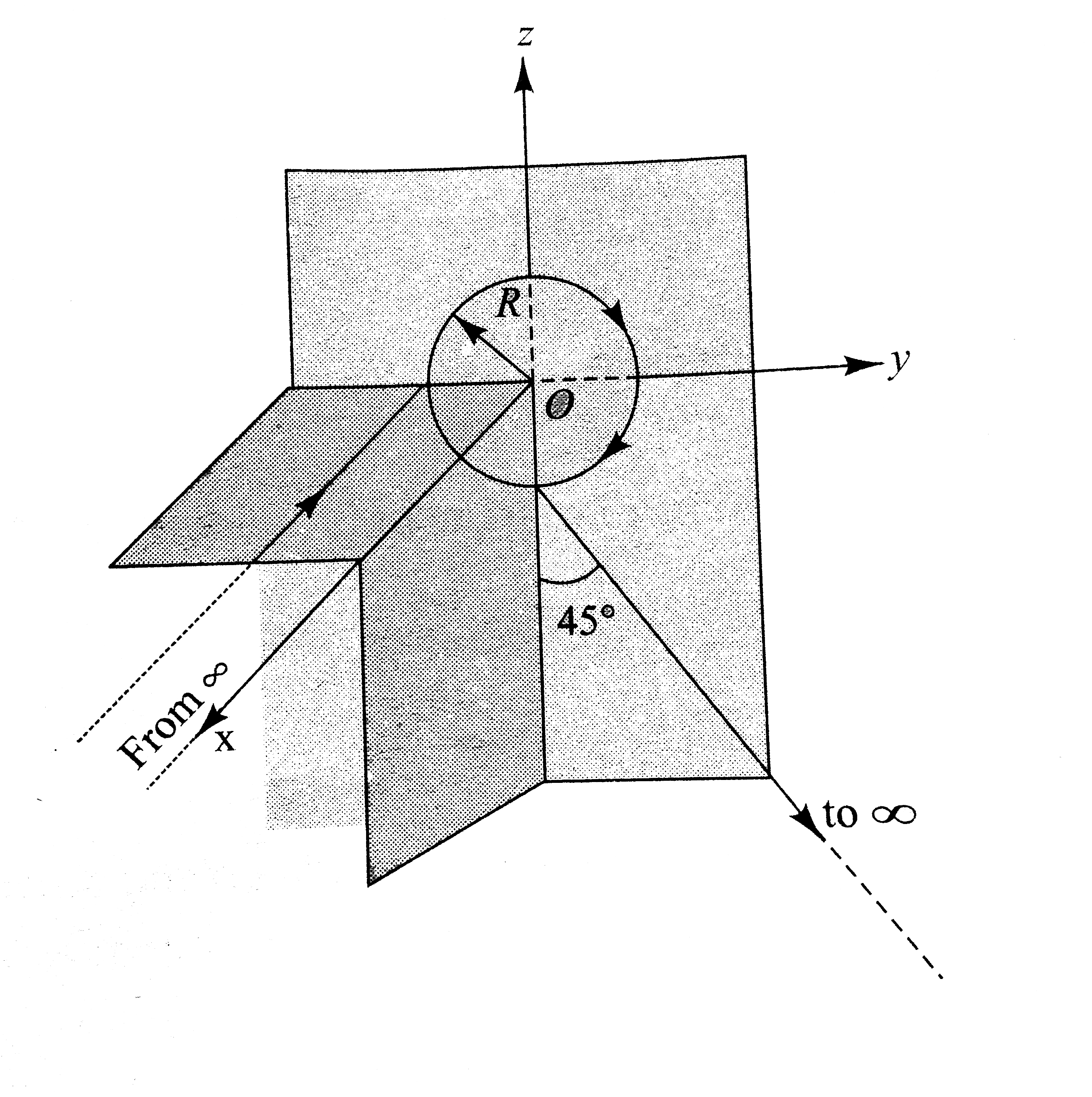
(The radius of the curved part of the wire is equal to R and linear parts of the wire are very long.)
View Solution
