A point chanrge of magnitude q=4.5nC is moving with speed v=3.6×107ms−1 parallel to the x-axis along the line y=3m. Find the magnetic field at the origin produced by this charge when the charge is at the point x=−4m, y=3m, as shown in Fig.

The magnetic field is given by
→B=μ04πq→v׈rr2, with →v=vˆi
→r=(4ˆi−3ˆj)m⇒→r=√42+32m=5m
Unit vector in the direction of ˆr=→r→r=4ˆi−3ˆj5=0.8ˆi−0.6ˆj
→v׈r=(vˆi)×(0.8ˆi−0.6ˆj)=−0.6vˆk
→B=μ04πq→v׈rr2=μ04πq(−0.6vˆk)r2
=−(10−7)(4.5×10−19)(0.6)(3.6×107)52ˆk
=−3.89×10−10Tˆk
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example
20 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.1
35 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
A particle of mass m=5 units is moving with a uniform speed v=3√2 units in the XY-plane along the y=x+4. The magnitude of the angular momentum about origin is
View SolutionA point charge q=−8.0nC is located at the origin. Find the electric field vector at the point x=1.2m,y=−1.6m.
View SolutionFind the magnitude of the electric field at a point 4 cm away from a line charge of density 2×10−6Cm−1.
View SolutionAs charge q=1μC is placed at point (1m,2m,4m). Find the electric field at point P(0,−4m,3m)
View SolutionRatio of electric and magnetic field due to moving point charge if its speed is 4.5×105m/s
View SolutionA charge q=−2.0μC is placed at origin. Find the electric field at (3m,4m,0).
View SolutionAn elevator carrying a charge of 0.5C is moving down with a velocity of 5×103ms−1. The elevator is 4m from the bottom and 3m horizontally from P as shown in Fig. What magnetic field (μT) does it produce at point P
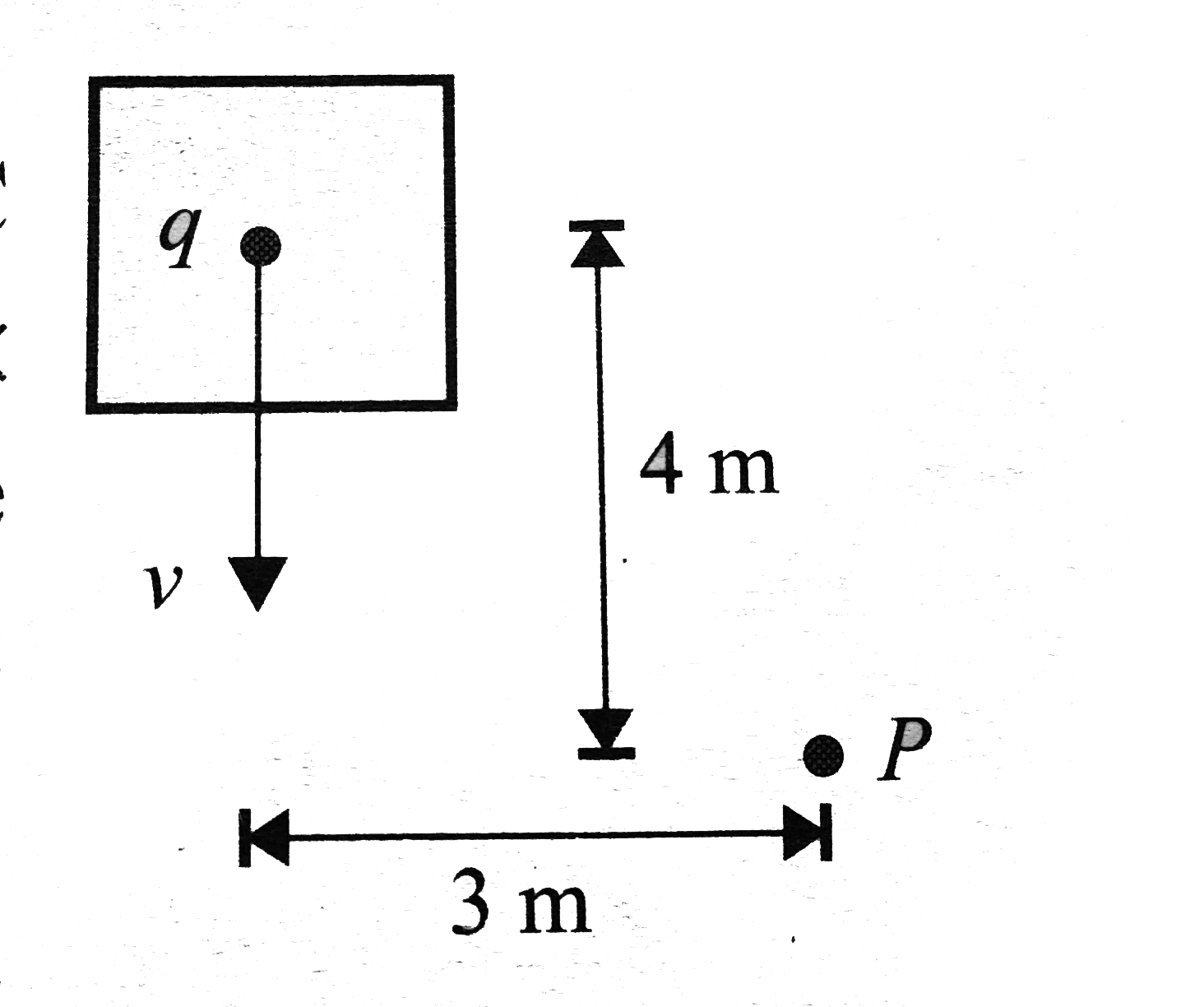
View SolutionAn infinite number of charges, each of coulomb, are placed along x-axis at x=1m,3m,9m and so on. Calculate the electric field at the point x = 0 due to these charges if all the charges are of the same sign.
View SolutionFind the points on the curve y=4x3−3x+5 at which the equation of the tangent is parallel to the X-axis.
View SolutionFind the equation of a line passing through the point (2,3) and parallel to the line 3x−4y+5=0 .
View Solution
