An object of height 2cm is kept 2m in front of a convex lens of focal length 1m. A plane mirror is placed at 3m from the lens on its other side. Find the nature, position, and magnification of the final image that will be seen by an observer looking toward the mirror through the lens.
To solve the problem step by step, we need to analyze the situation involving the convex lens and the plane mirror. Here’s how we can approach it:
Step 1: Identify the parameters of the lens and object
- Object height (h): 2 cm
- Object distance from the lens (u): -2 m (the negative sign indicates that the object is on the same side as the incoming light)
- Focal length of the lens (f): +1 m (positive for a convex lens)
Step 2: Use the lens formula to find the image distance (v)
The lens formula is given by:
1f=1v−1u
Substituting the known values:
11=1v−1−2
This simplifies to:
1=1v+12
Rearranging gives:
1v=1−12=12
Thus,
v=2 m
This means the image is formed 2 m on the opposite side of the lens.
Step 3: Determine the nature and position of the image formed by the lens
Since the object is at 2 m and the image is also at 2 m on the opposite side, the image is:
- Nature: Real and inverted (since it is formed by a convex lens).
- Position: 2 m from the lens on the opposite side.
Step 4: Consider the plane mirror
The plane mirror is placed 3 m from the lens. The image formed by the lens (2 m from the lens) will act as an object for the mirror. The distance from the image to the mirror is:
Distance from image to mirror=3 m−2 m=1 m
The mirror will form an image of this object (the image formed by the lens) at the same distance behind the mirror, which is 1 m.
Step 5: Calculate the position of the final image
The final image position relative to the lens is:
Distance from lens to mirror+Distance from mirror to final image=3 m+1 m=4 m
Thus, the final image is formed at +4 m (on the same side as the object).
Step 6: Calculate the magnification
The magnification (M) for the lens is given by:
M=h′h=−vu
Substituting the values:
M1=−2−2=1
The image formed by the lens is of the same size as the object but inverted.
For the mirror, the magnification is also 1 (it does not change the size, just reflects the image).
Step 7: Total magnification
The total magnification is given by:
Mtotal=M1×M2
Where M2 is the magnification due to the mirror, which is also 1. Therefore:
Mtotal=1×1=1
Final Result
- Nature of the final image: Real and inverted
- Position of the final image: 4 m from the lens
- Magnification: 1 (same size as the original object)
- Object height (h): 2 cm
- Object distance from the lens (u): -2 m (the negative sign indicates that the object is on the same side as the incoming light)
- Focal length of the lens (f): +1 m (positive for a convex lens)
The lens formula is given by:
1f=1v−1u
Substituting the known values:
11=1v−1−2
This simplifies to:
1=1v+12
Rearranging gives:
1v=1−12=12
Thus,
v=2 m
This means the image is formed 2 m on the opposite side of the lens.
Since the object is at 2 m and the image is also at 2 m on the opposite side, the image is:
- Nature: Real and inverted (since it is formed by a convex lens).
- Position: 2 m from the lens on the opposite side.
The plane mirror is placed 3 m from the lens. The image formed by the lens (2 m from the lens) will act as an object for the mirror. The distance from the image to the mirror is:
Distance from image to mirror=3 m−2 m=1 m
The mirror will form an image of this object (the image formed by the lens) at the same distance behind the mirror, which is 1 m.
The final image position relative to the lens is:
Distance from lens to mirror+Distance from mirror to final image=3 m+1 m=4 m
Thus, the final image is formed at +4 m (on the same side as the object).
The magnification (M) for the lens is given by:
M=h′h=−vu
Substituting the values:
M1=−2−2=1
The image formed by the lens is of the same size as the object but inverted.
The total magnification is given by:
Mtotal=M1×M2
Where M2 is the magnification due to the mirror, which is also 1. Therefore:
Mtotal=1×1=1
- Nature of the final image: Real and inverted
- Position of the final image: 4 m from the lens
- Magnification: 1 (same size as the original object)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Solved Examples
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.1
14 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
Knowledge Check
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirror
An object of height 2 cm is placed in front of a convex lens of focal length 20 cm at a distance of 15 cm from it. Find the position and magnification of the image.
View SolutionA point like object is placed at a distance of 1 m in front of a convex lens of focal length 0.5 m . A plane mirror is placed at a distance of 2 m behind the lens. The position and nature of the final image formed by the system is :
View SolutionL is a lens such that a parallel beam of light I ncident on it, after refraction, converges to a point at a distance x from it and M is a mirror such that a parallel lbeam of light incident on it, after reflection, converges to a point at a distance y from it. Now the lens L and mirror M are placed at a distan 2(x+y) from each other. An object of size 2 cm is kept infront of lens at a distance 2x from it. Find the nature, position , and size of the image that willl be seen by an observer looking toward the mirror through the lens.
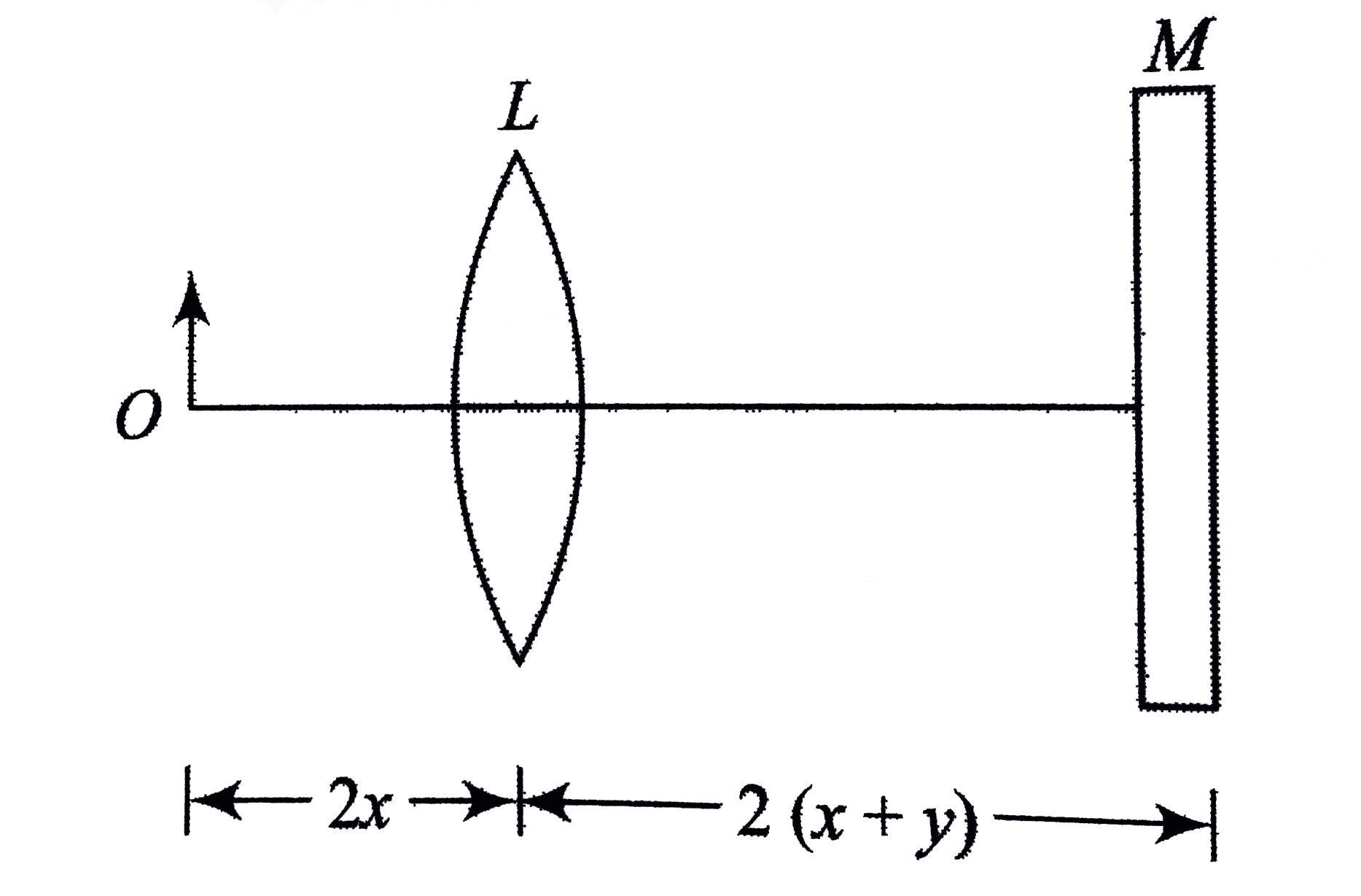
View SolutionThe plane surface of a plano-convex lens of focal length 60 cm is silvered. A point object is placed at a distance 20 cm from the lens. Find the position and nature of the final image formed.
View SolutionAn object of height 2 cm is placed at a distance 20cm in front of a concave mirror of focal length 12 cm. Find the position, size and nature of the image
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
nature of the image
View SolutionFind distanace of image from a convex lens of focal length
20cm if object is placed at a distance of 30cm from the lens. Also find its
magnification.
View Solution

_E01_080_Q01.png)