Shown in figure is a Post Office box. In order to calculate the value of external resistance, it should be connected between
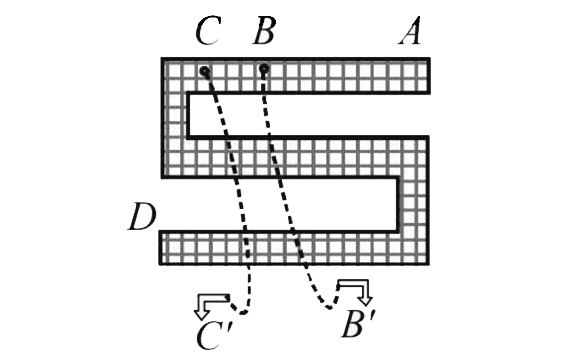
B'andC'
AandD
CandD
BandD
The correct Answer is:B
b. Total external resistance will be the total resistance of whole
length of the box. It should be connected between A and D.
Similar Questions
For the post office box arrangement to determine the value of unknown resistance, the unknown resistance should be connected between,
(a) B and C
(b) C and D
(c) A and D
(d) B1 and C1 .
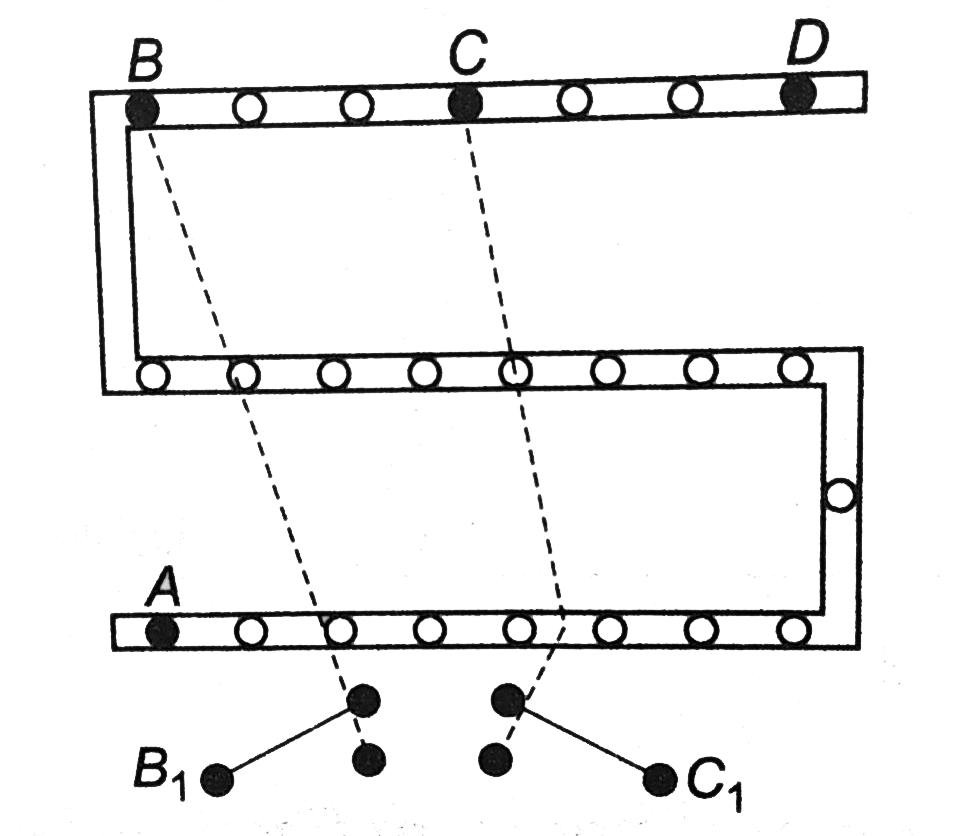 .
.
View SolutionFor the post office arrangement to determine the value of unknown resistance, the unknown resistance should be connected between.
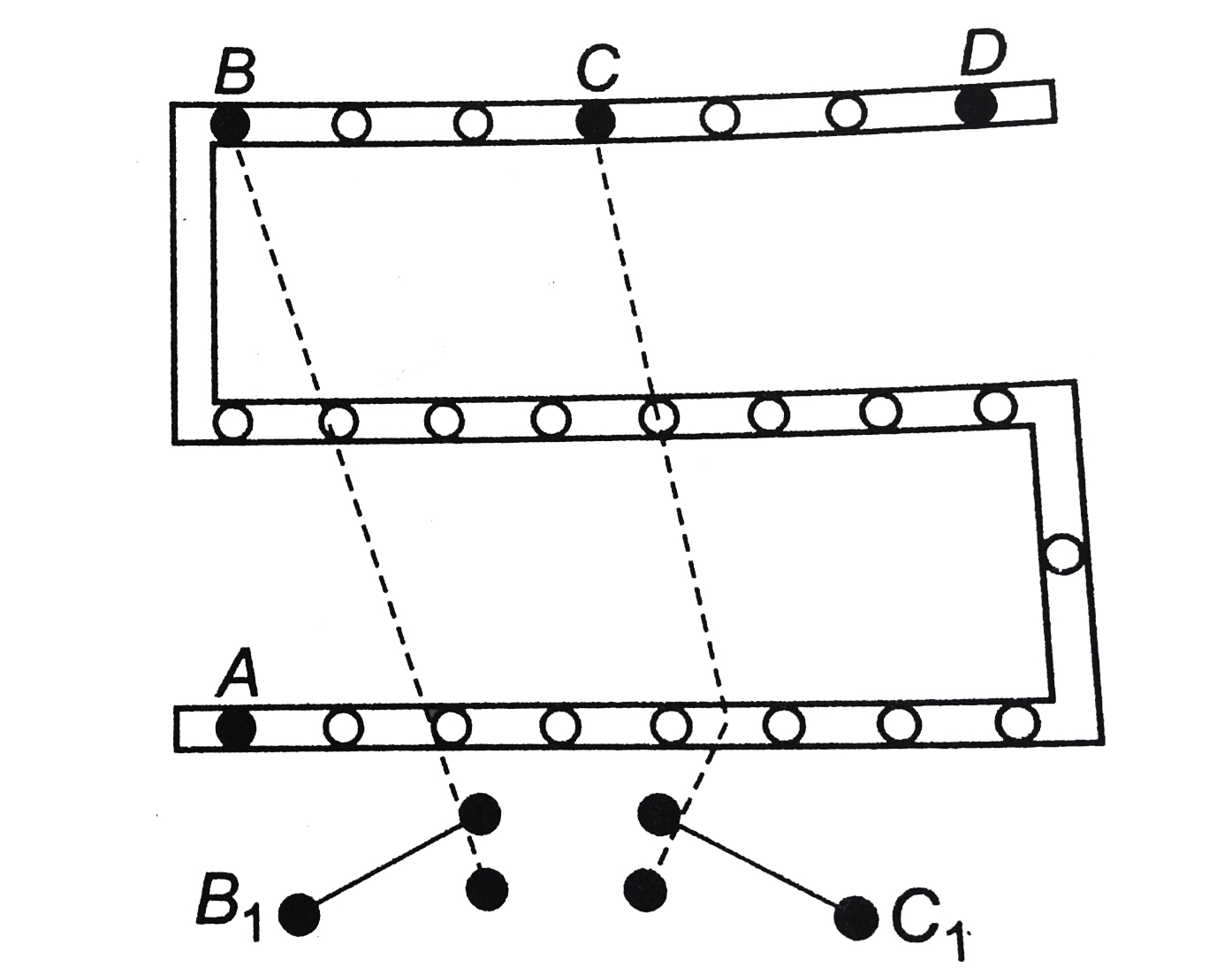
View SolutionIn an experiment with a post office box, the radio of arms are 1000:10. If the value of the third resistance is 999Ω, find the unknows resistance.
View SolutionIn a post office box if the position os the cell and the galvenometer are interchangd, then the:
View SolutionIn the circuit shown in figure points a, b and c are maintained at constant (but may be different) potentials. When a resistance is connected between a and b no current flows through it, when the same resistance is connected between b and c current flows from c to b.
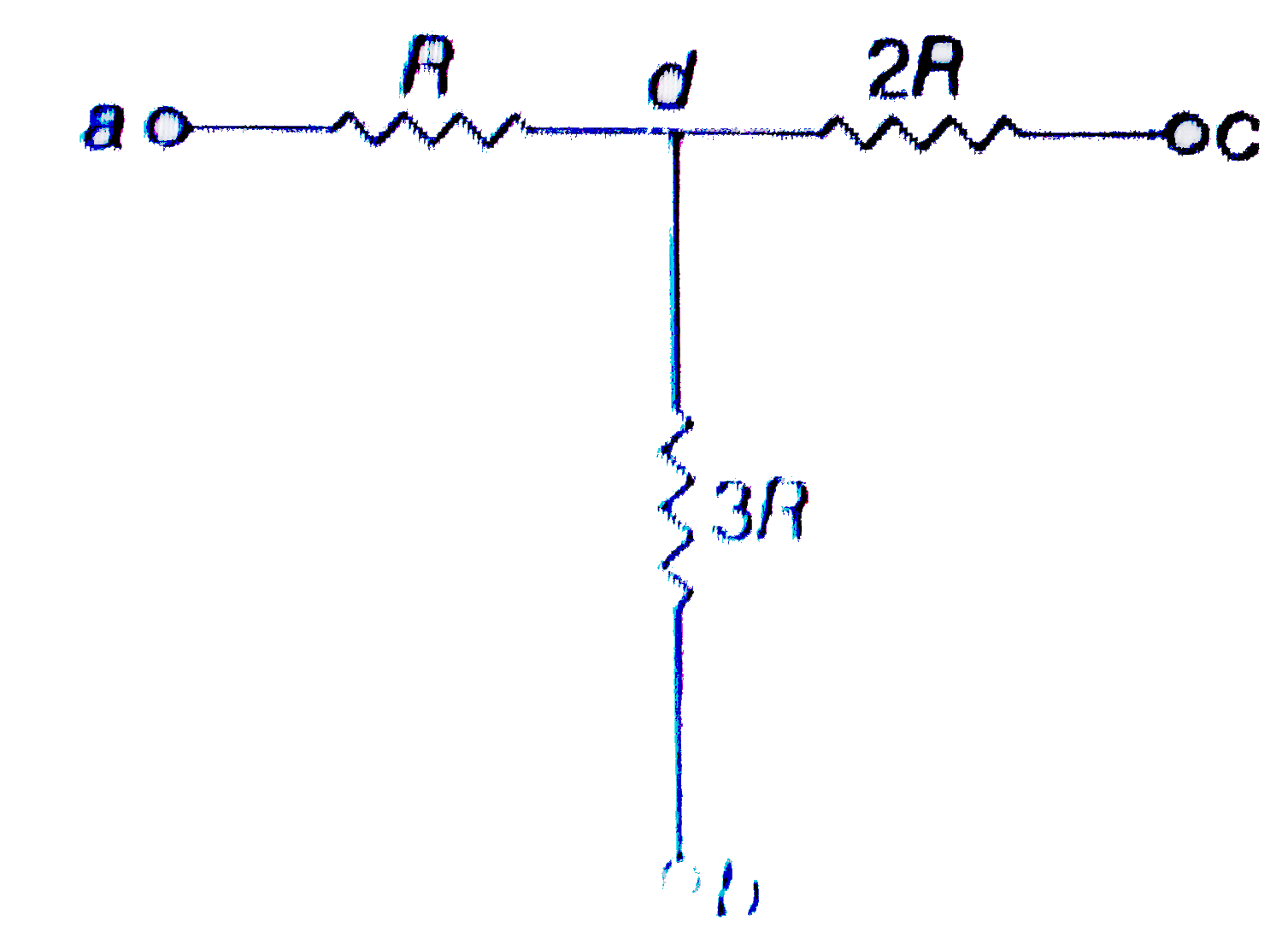
When only three resistance shown in figure are in the circuit
View Solution(a) Draw graph showing the variation of current versus voltage in an electroyte when an external resistance is also connceted.
(b) (i) The graph between resistance (R ) and temperature (T) for Hg is shown in the figure (a). Explain the behaviour of Hg near 4k.
(ii) In which region of the graph shown in the figure (b) is the resistance negative and why?

View SolutionPoint a in the figure shown is maintained at potential of 300V. The reading of a voltmeter of a resistance 3×104Ω, when connected between point b and ground is
_PHY_E05_299_Q01.png)
View Solutionthe post office box works on the peinclple of :
View SolutionA battery of internal resistance 4Ω is connected to the network of the resistance as shown in figure . If the maximum power can be delivered to the network, the magnitude of resistance in Ωshould be
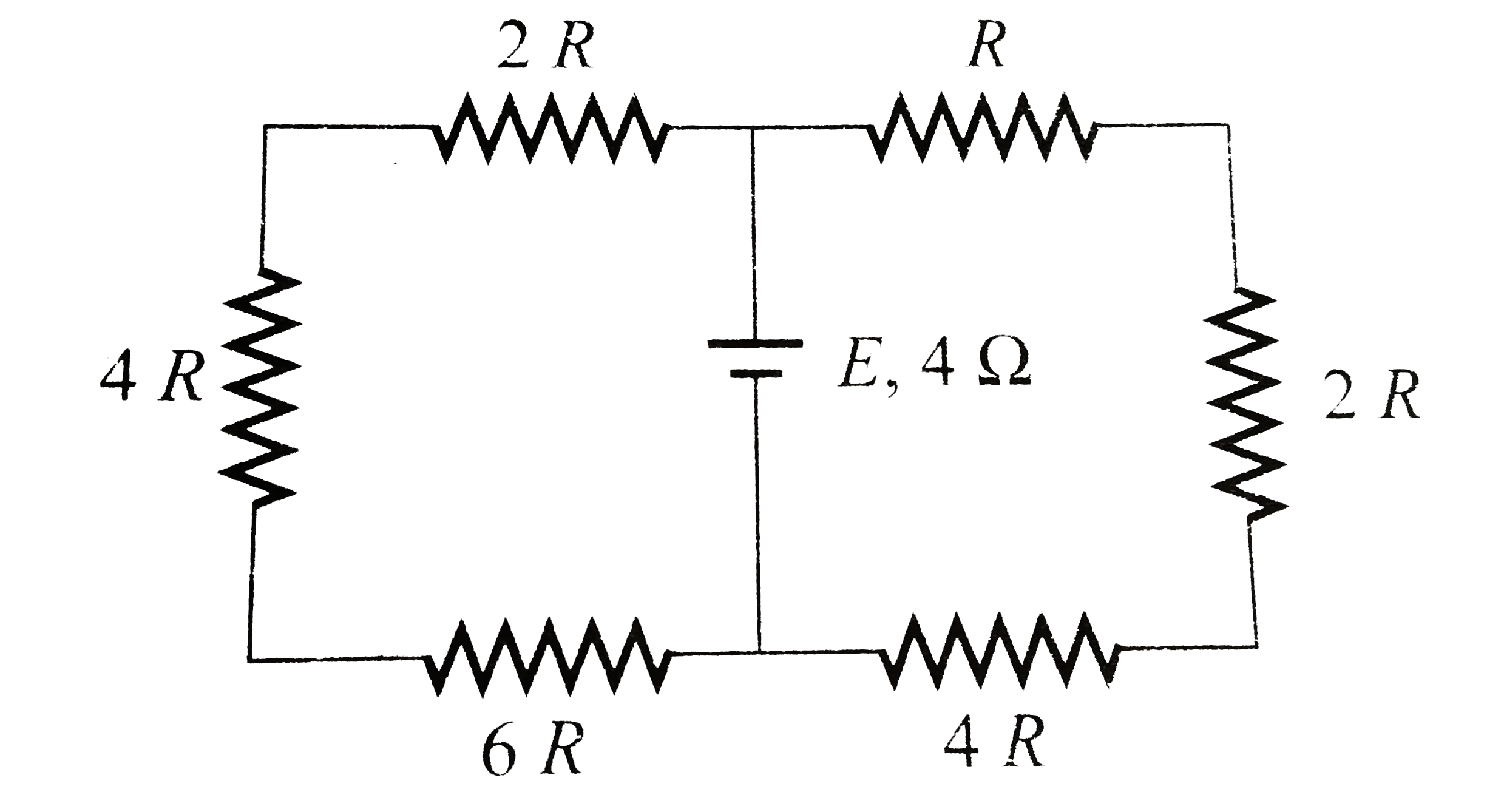
View SolutionIn the circuit shown in Fig. (b) calculate the equivalent resistance between the points A and B.
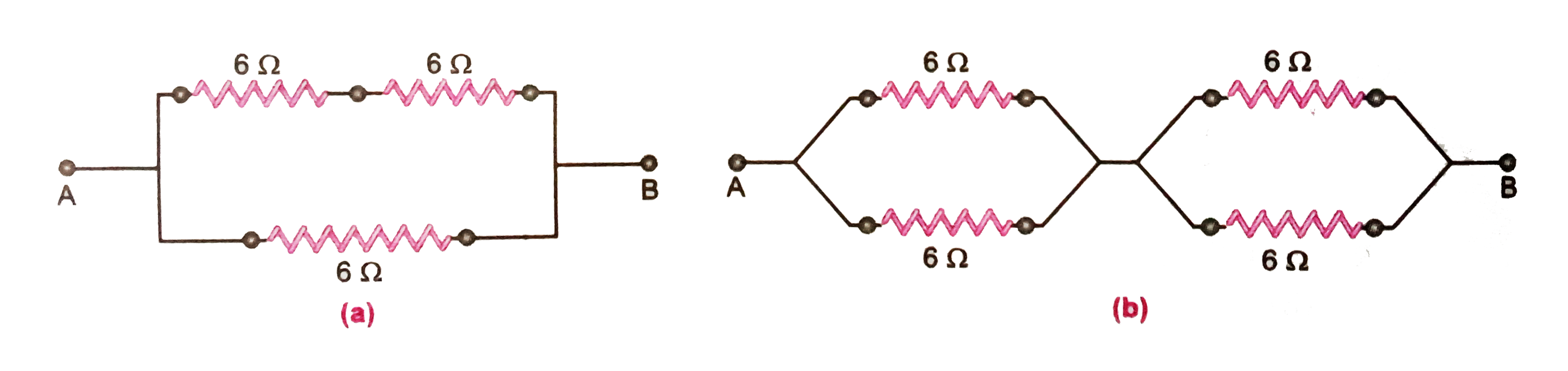
View Solution
