In the circuit shown, all capacitors are identical. Initially, the switch is open and the capacitor marked is the only one charged to a value . After the switch is closed and the equilibrium is reestablished, the charge on the capacitor marked is Q. Find the ratio initial change to final charge in capacitor .
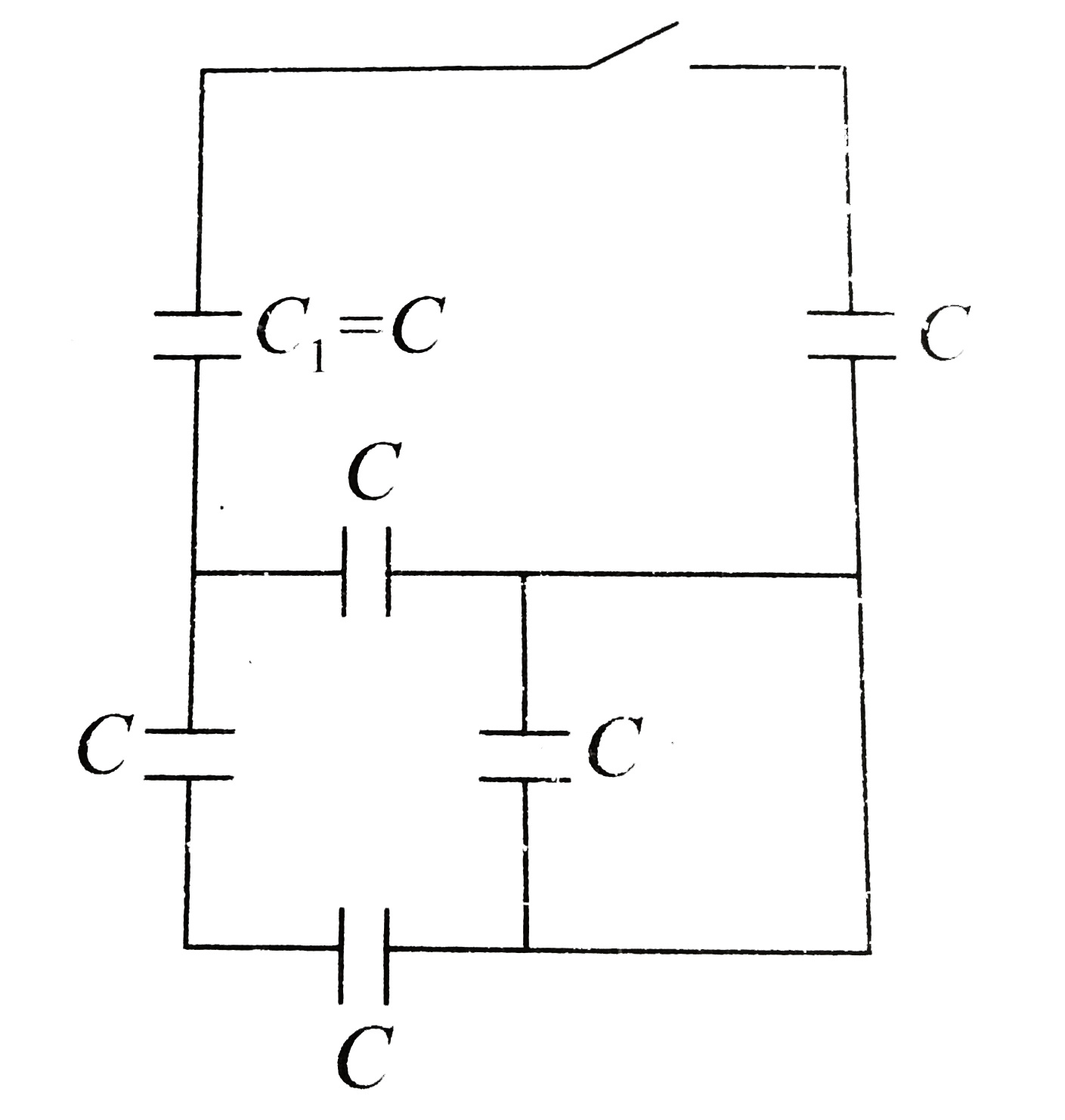
We begin with the circuit given, assigining names to each identical capacitor. begins with an unknown initial charge and achieves a charge after the circuit is connected and has re-established equilibrium.

As is clearly shorted, the potential difference across its plates is , and as such the capacitor will contain no charge and will not afect the circuit We can therefore remove it from the schematic. This simplified circuit can be broken down into even simpler equivalne tcircuits. Leaving where it is, and recognizing and in series with each other *yielding an equivalent capacitance of ), and together in parallel with , Acknowledging the combined capacitors are equal, must have an equivalent capacitance of , As is simply in series with , the resultant equivalent circuit has simply one capacitor in series with , where must have an equivalent capacitance of ,
Since
where is the potential difference across is the potential difference across , and is the charge on For equilibrium conditions, . Therefore,
by the conservation of charge,
.
The initial charge on the capacitor was of the final charge on the capacitor after the switch was closed.

Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Fill in the blanks
10 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False Type
5 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type
94 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
Condsider
 .
.
The charge on capacitor C1 is.
View SolutionThe circuit is in a steady state.
The charge in capacitor C1 is
View SolutionIn the given figure switch is open initially and capacitor C2 is unchanged
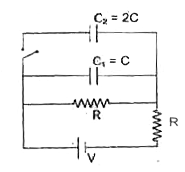
Charge on C2 just after closing the switch is
View Solution
In the circuit shown, all the capacitors are initially uncharged. The current through the battery just after closing the switch 'S' is
View SolutionInitially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View SolutionIn the circuit shown in fig. when the switch is closed, the capacitor charges with a time constant
View SolutionIn the circuit shown, charge on the capacitor connected between B and D at steady state is (initially all the capacitors are uncharged)

View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant

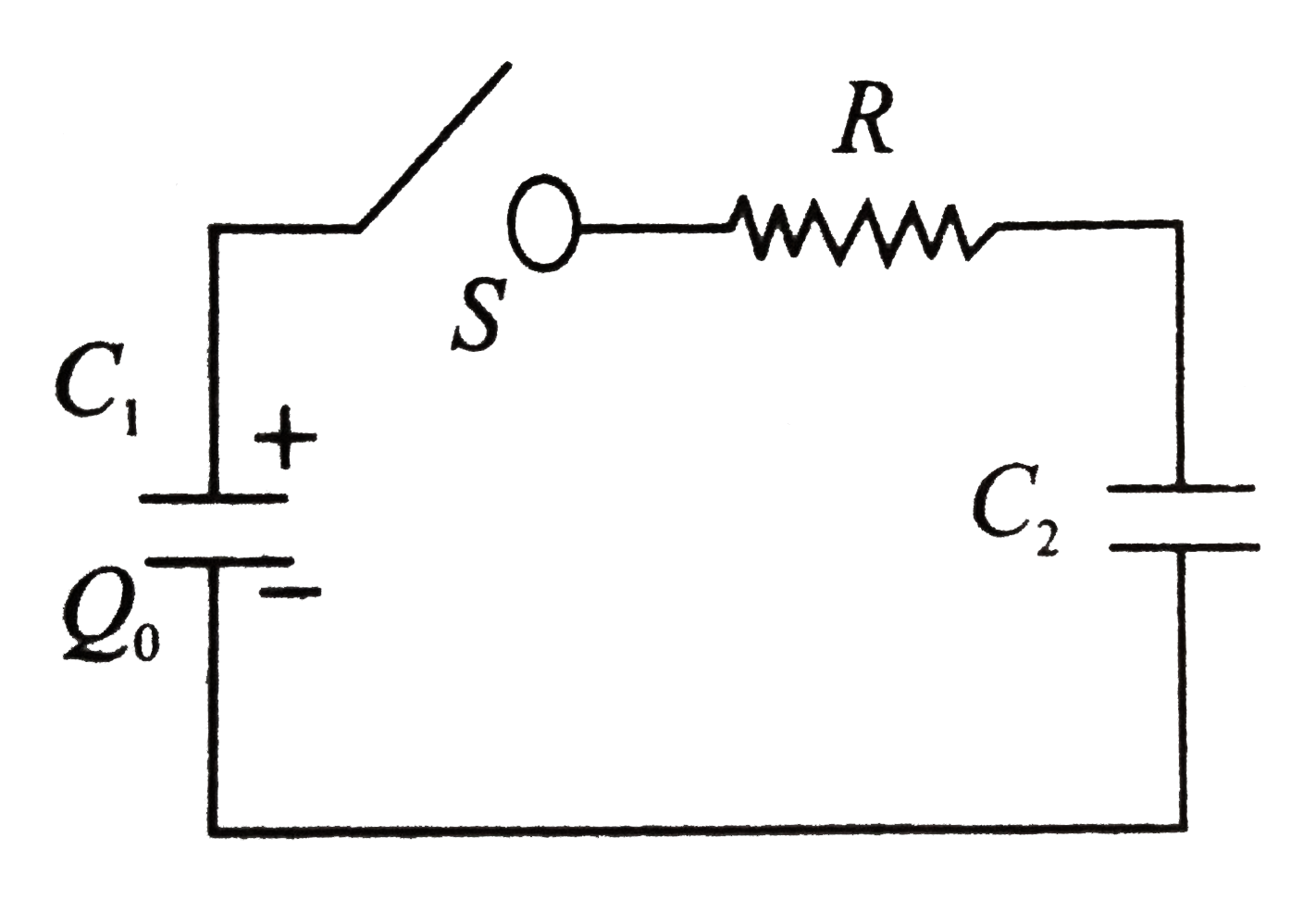
View SolutionIn the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
View SolutionIn the circuit shown in figure, the capacitor is charged with a cell of 5V.If the switch is closed at t=0, then at t=12s, charge on the capacitor is

View Solution
