At a distance r from a point located at origin in space, the electric potential varies as V=10r. Find the electric field at →r=3ˆi+4ˆj−5ˆk.
(√2)(3ˆi+4ˆj−5ˆk)
(−√2)(3ˆi+4ˆj−5ˆk)
(−√3)(3ˆi+4ˆj−5ˆk)
none of these
The correct Answer is:B
To solve the problem, we need to find the electric field →E at the point given by the vector →r=3^i+4^j−5^k when the electric potential V varies as V=10r, where r is the distance from the origin.
Step 1: Express r in terms of coordinates
The distance r from the origin to the point (x,y,z) is given by:
r=√x2+y2+z2
For our point →r=3^i+4^j−5^k:
- x=3
- y=4
- z=−5
Calculating r:
r=√32+42+(−5)2=√9+16+25=√50
Step 2: Write the potential V
Substituting r into the potential equation:
V=10r=10√50=10×5√2=50√2
Step 3: Calculate the electric field →E
The electric field →E is related to the electric potential V by the equation:
→E=−∇V
In Cartesian coordinates, this can be expressed as:
→E=−(∂V∂x^i+∂V∂y^j+∂V∂z^k)
Step 4: Calculate the partial derivatives
First, we need to express V in terms of x,y,z:
V=10√x2+y2+z2
Now, we compute the partial derivatives:
1. For ∂V∂x:
∂V∂x=10⋅x√x2+y2+z2=10⋅xr
2. For ∂V∂y:
∂V∂y=10⋅y√x2+y2+z2=10⋅yr
3. For ∂V∂z:
∂V∂z=10⋅z√x2+y2+z2=10⋅zr
Step 5: Substitute values of x,y,z
Now substituting x=3, y=4, and z=−5:
- r=√50
Calculating the components of →E:
1. For Ex:
Ex=−∂V∂x=−10⋅3√50=−30√50=−305√2=−6√2=−3√2
2. For Ey:
Ey=−∂V∂y=−10⋅4√50=−40√50=−405√2=−8√2=−4√2
3. For Ez:
Ez=−∂V∂z=−10⋅−5√50=50√50=505√2=10√2=5√2
Step 6: Write the electric field vector
Combining the components, we get:
→E=−3√2^i−4√2^j+5√2^k
Final Answer
→E=−3√2^i−4√2^j+5√2^k
The distance r from the origin to the point (x,y,z) is given by:
r=√x2+y2+z2
For our point →r=3^i+4^j−5^k:
- x=3
- y=4
- z=−5
r=√32+42+(−5)2=√9+16+25=√50
Substituting r into the potential equation:
V=10r=10√50=10×5√2=50√2
The electric field →E is related to the electric potential V by the equation:
→E=−∇V
In Cartesian coordinates, this can be expressed as:
→E=−(∂V∂x^i+∂V∂y^j+∂V∂z^k)
First, we need to express V in terms of x,y,z:
V=10√x2+y2+z2
Now, we compute the partial derivatives:
∂V∂x=10⋅x√x2+y2+z2=10⋅xr
∂V∂y=10⋅y√x2+y2+z2=10⋅yr
∂V∂z=10⋅z√x2+y2+z2=10⋅zr
Now substituting x=3, y=4, and z=−5:
- r=√50
1. For Ex:
Ex=−∂V∂x=−10⋅3√50=−30√50=−305√2=−6√2=−3√2
Ey=−∂V∂y=−10⋅4√50=−40√50=−405√2=−8√2=−4√2
Ez=−∂V∂z=−10⋅−5√50=50√50=505√2=10√2=5√2
Combining the components, we get:
→E=−3√2^i−4√2^j+5√2^k
→E=−3√2^i−4√2^j+5√2^k
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type
94 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
Let V0 be the potential at the origin in an electric field →E=4ˆi+5ˆj. The potential at the point (x,y) is
View SolutionThe variation of potential with distance R from the fixed point is shown in (Fig. 3.125).
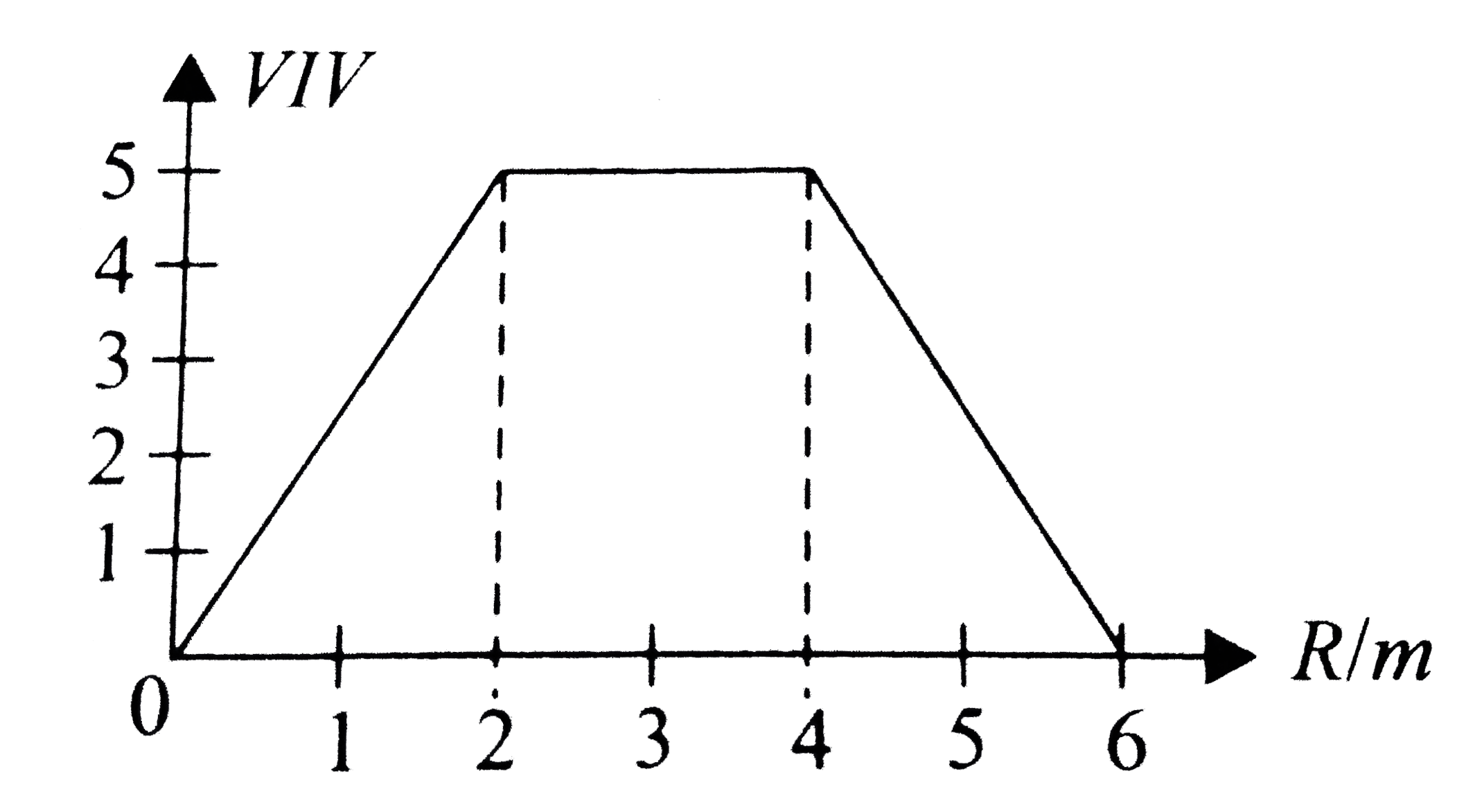 .
.
The electric field at R=5m is.
View SolutionThe variation of potential with distance r from a fixed point is shown in fig. The electric field at r = 5cm, is :

View SolutionThe variation of potential with distance R from a fixed point is shown in figure. The electric field at R = 5 m is -
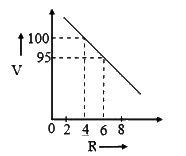
View SolutionA positive charge 50 muC is located in xy plane at a position vector r0=4ˆi+4ˆj. the electric field strength E at a point whose position vector is →r=10ˆi−4ˆj is (→r0 and →r are expressed in metre)
View SolutionThe work done in moving an object from origin to a point whose position vector is →r=3ˆi+2ˆj−5ˆk by a force →F=2ˆi−ˆj−ˆk is
View SolutionElectric field in a region of space is radially outward from origin and varies with distance 'r' from origin as E = kr. Find the charge enclosed in a sphere of radius 'a' centred at origin.
View SolutionLet V0 be the potential at the origin in an electric field →E=Exˆi+Eyˆj. The potential at the point (x,y) is
View SolutionFind the image of the point having position vector ˆi+3ˆj+4ˆk in the planer. →r.(2ˆi–ˆj+ˆk)+3=0
View SolutionAssertion: Electric potential on the surface of a charged sphere of radius R is V. Then electric field at distance r=R2 from centre is V2R. Charge is distributed uniformly over the volume.
Reason: From centre to surface, electric field varies linearly with r. Here r is distance from centre.
View Solution
