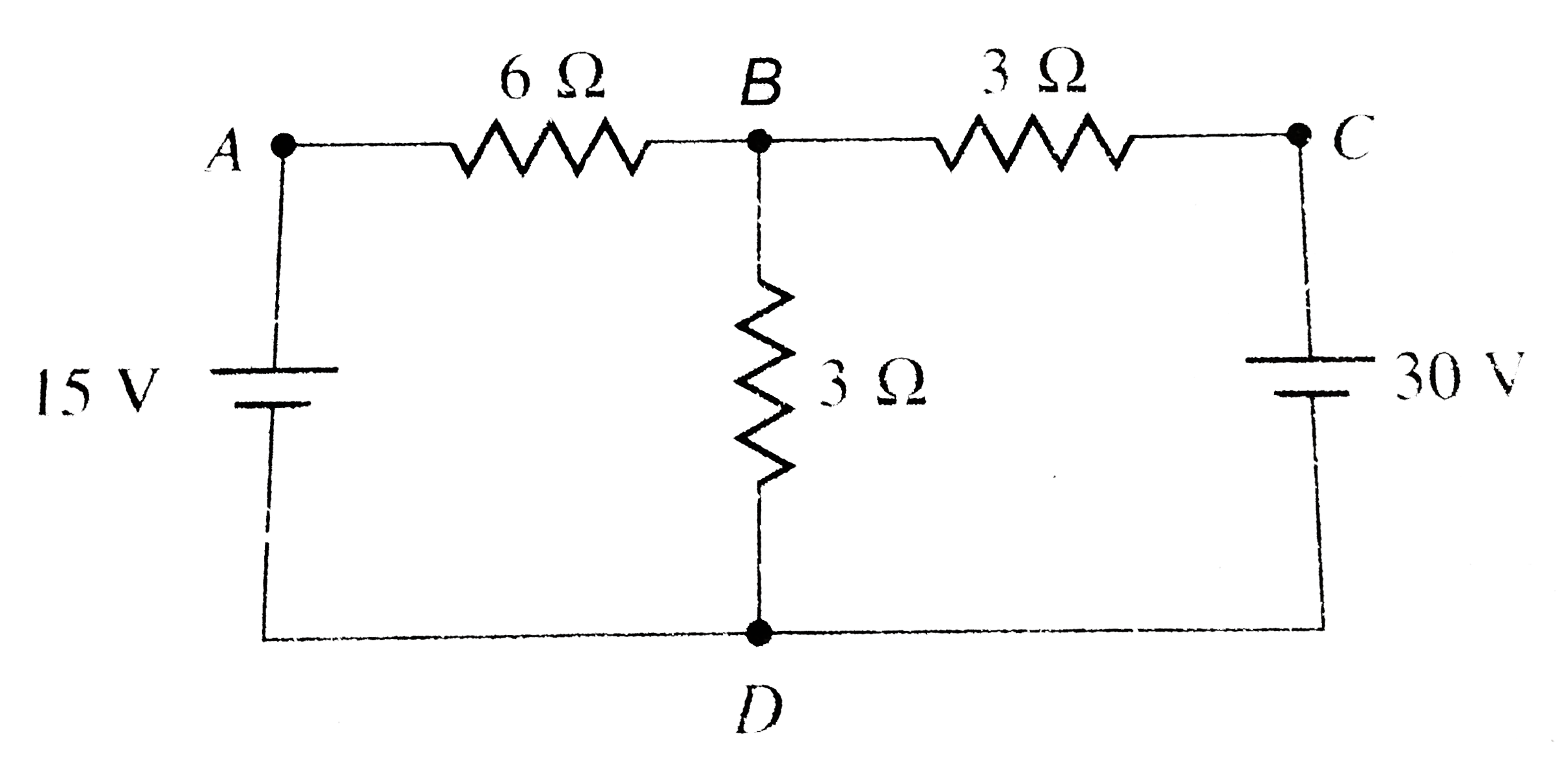
In the circuit shown in figure, find the current through the branch BD.
2 A
3 A
4 A
5 A
The correct Answer is:D
Method 1 : Using Kirchhoff's law M The currents in the circuit are assumed as shwon in fing Applying KVL along the loop ABDA, we get
or
Applying KVL along the loop BCDB, we get
or
Solving Eqs. (i) and (ii) for .
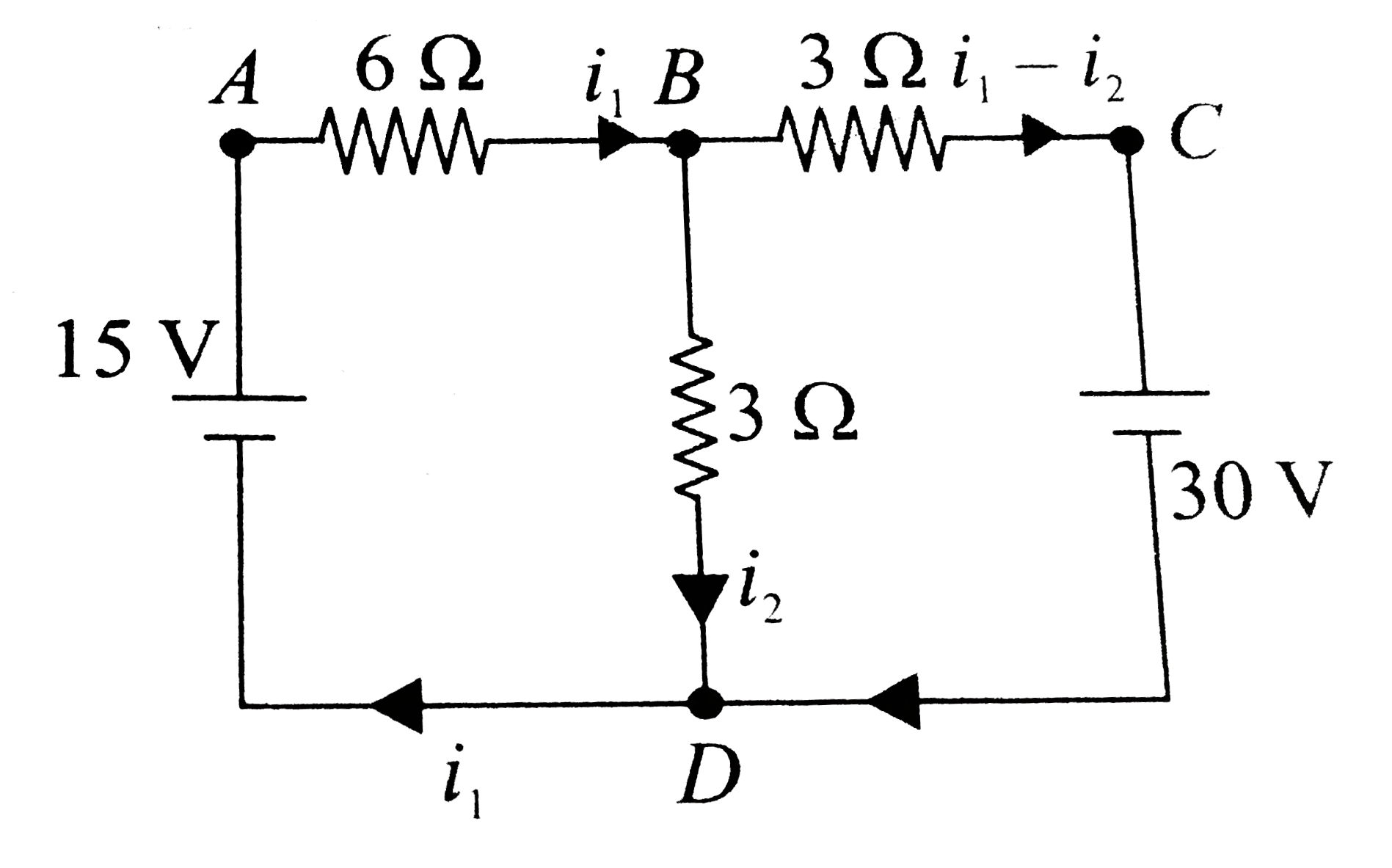
Method 2: using equivalnet battery method (i)
we can treat resistance connected with 15V
and 30V batteries, respectively, as internal resistances of the
batteries. Now we can assume these batteries are connected in
parallel, and equivalnet battery of these two is connected with
resistance connected across B and D.


Hence, current through resistace connected across B and
D is
Method 3: Using equivalent battery method (ii)
We cna assume a battery of zero emf is connected in series
with resistance connected across BD. This resistance can be
treated as internal resistance of zero emf battery. Now we have
three battery which is the open cirucuit.
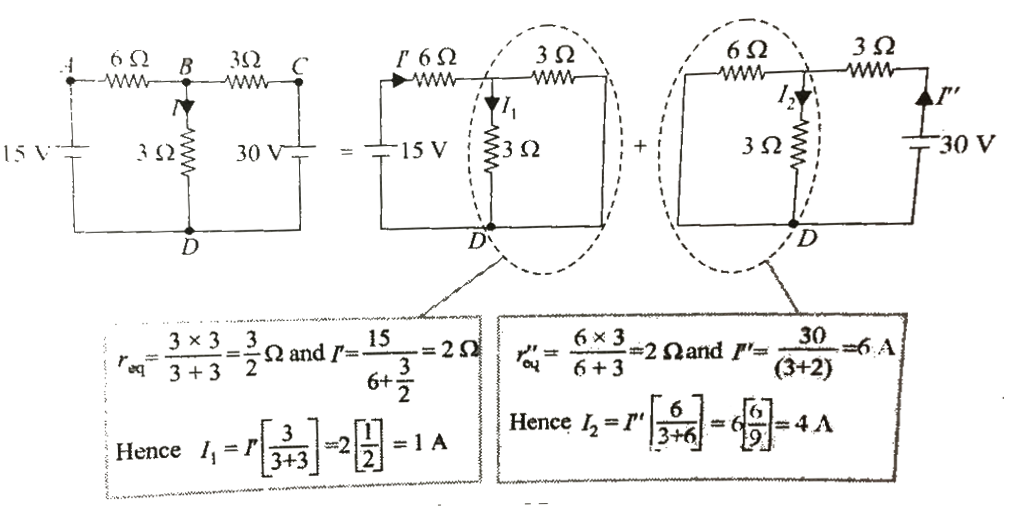
As equivalent battery in as open circuit, the potential
difference across each of the battery branch wikll be 15V.
Hence, current through the resistacne connected across BD is
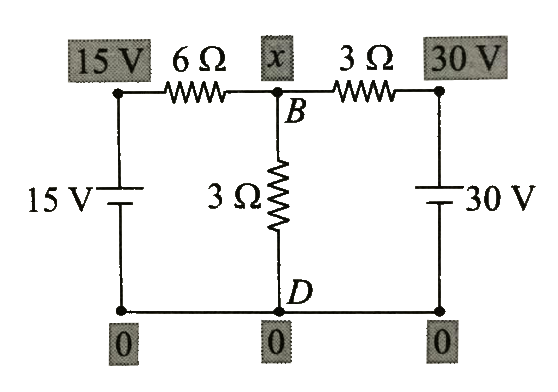
Method 4 : Using nodal method
Let us asume the potential of node D zero and the potential of node B x. then we can assign the potentials at different nodes
as shown in fig 5.124. At node B,
Hence current through resistacne connected across BD is

Method 5: using superposition principle In superposition method, we can take the effect of one battery at a time. From fig, it is clear that the effect on two
batteries can be taken by adding the effect of individual batteries.



Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples12videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.128videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
In the circuit shown in the figure, the current through the
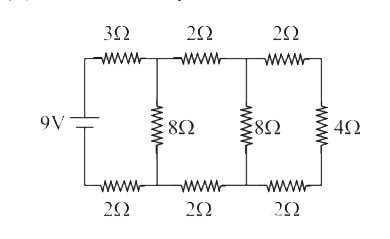 View Solution
View SolutionIn the circuit shown in find the current throught the bracnh BD.
 View Solution
View SolutionIn the circuit shown in figure the current through
 View Solution
View SolutionIn the circuit shown in figure ,
a. find the current is each branch
b. find the potential difference Vab of point a relative to point b.View SolutionConsider the circuit shown in figure.(a) find the current through the battery a long time after the switch S is closed. (b) Suppose the switch is again opened at t = 0. What is the time constant of the discharging circuit? (c ) Find t current through the inductor after one time constant.
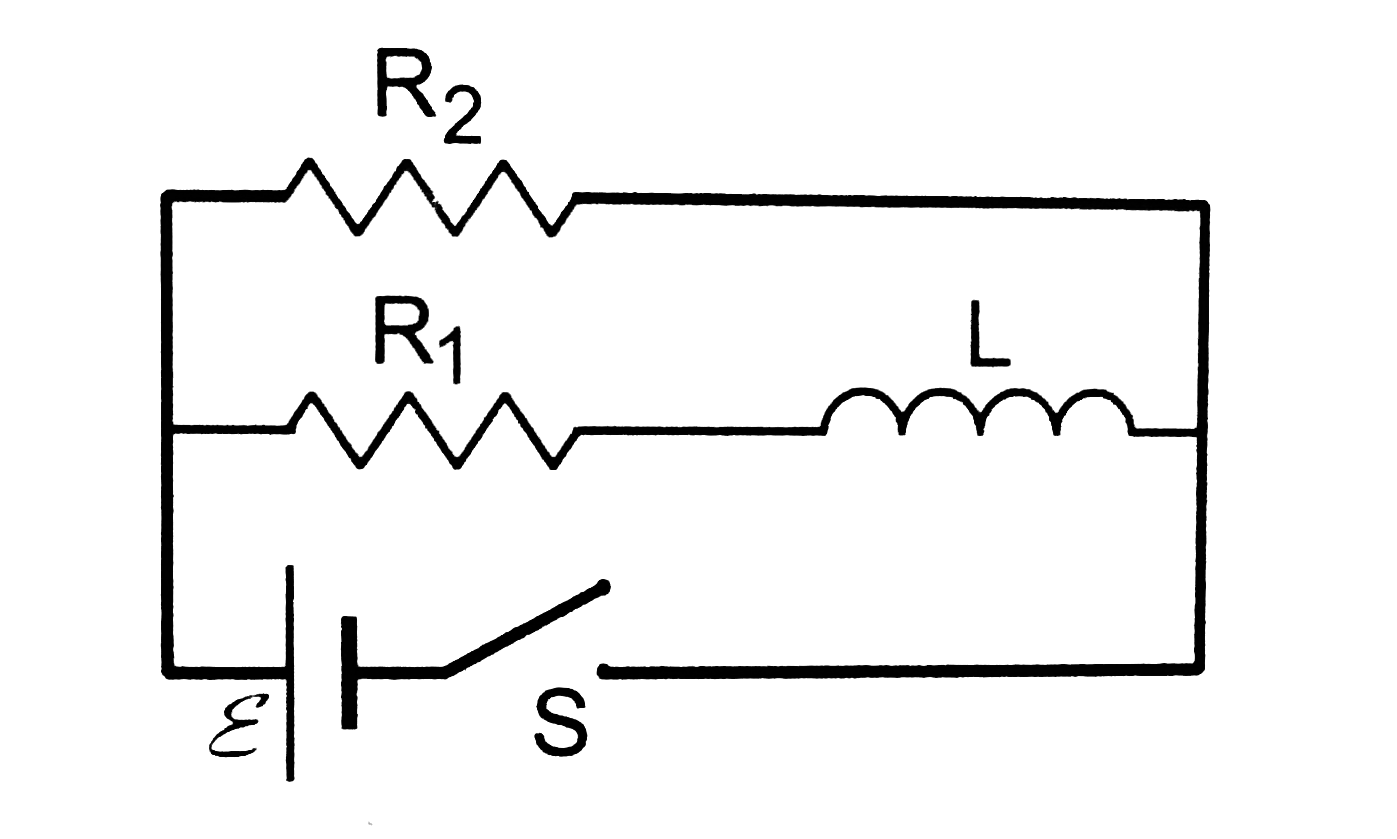 View Solution
View SolutionThe circuit shown in figure, find the current through wire XY in ampere
 View Solution
View SolutionFor the circuit shown in figure, find
(a) the initial current through each resistor
(b) steady state current through each resistor
(c) final energy stored in the capacitor
(d) time constant of the circuit when switch is opened.
 View Solution
View SolutionFor the circuit shown in figureure, find the instaneous current through each element.
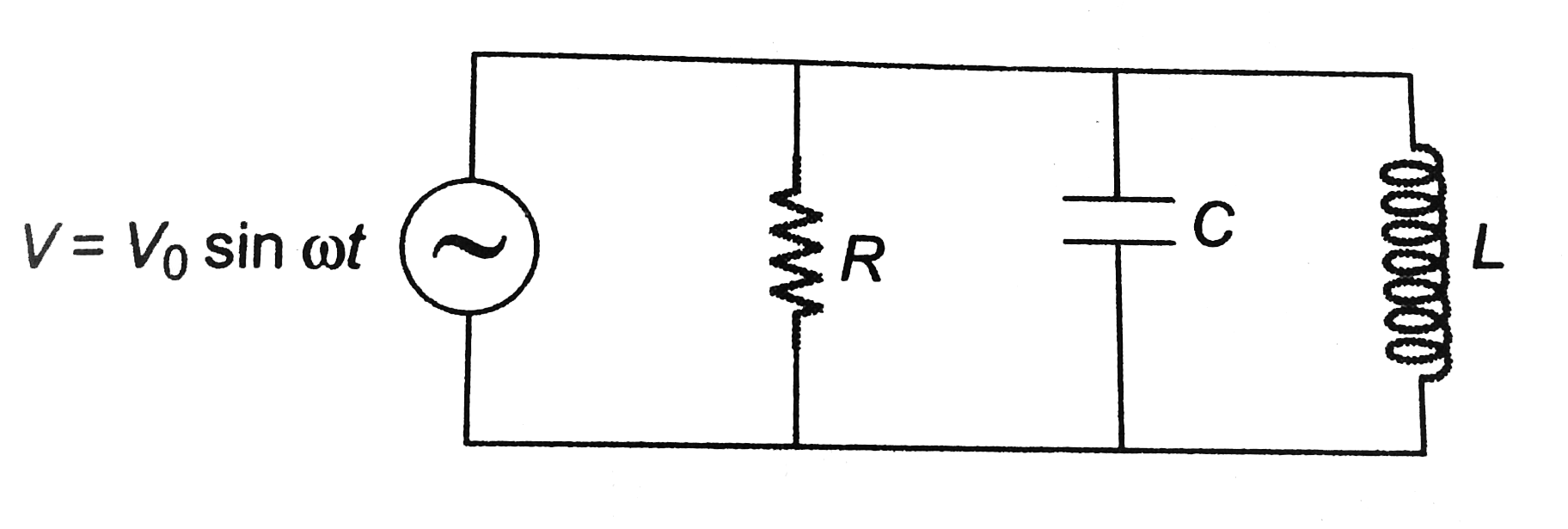 .View Solution
.View SolutionFor the circuit shown in figureure, find the instaneous current through each element.
 .View Solution
.View SolutionIn the circuit shown in figure, the current / in circuit is
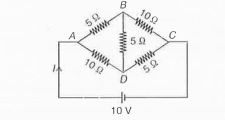 View Solution
View Solution
