Each of the three plates shown in figure has an area of 200 cm^2 on one side and the gap between the adjacent plates is 0.2 mm. The emf of the battery is 20V. Find the distribution of charge on various surfaces of the plates. What is the equivalent capacitance of the system between the terminal points?

As the potentials of a and c are equal, the capacitors Cab and Cbc are in parallel. Therefore,
Cab=Cbc=ε0Ad=ε0×2×10−20.2×10−3=100ε0(F)
Equivalent capacitance is
C=Cab+Cbc=2ε0Ad
=2×ε×2×10−20.2×10−3=200ε0(C)
The charge on plat b is negetive on both faces. Thus, the charge on faces a and c is  .
.
qa=qc=ε0Adε
=100ε0×20
=2000ε0(C)
∴Q=2×2000ε0(C)
=4000ε0(C)
Alternative method : Let us assume that the potential of the middle plate be zero, Then the potential of the left and right plates will be 20V each. Let the positive terminal of the battery lupply a charge Q . This charge is divided into two plates as shown in. The charge on the outermost surfaces will be zero,
 .
.
Equal and opposite charges will appear on both surfaces of the mid plate (pate2).The sum of the charges on both the surfaces should be −Q, which will flow toward the negative terminal of the battery. we can observe two capacitors C1 and C2 for capacitor C1
x=C(20−0) (i)
For capacitor C2
(Q−x)=C(20−0) (ii)
From (i)
x=ε0Ad×20=ε0(2×10−2)0.2×10−3×20=2000ε0(C)
Also from (ii)
(Q−x)=2000ε0(C)
The net charge on the mid plate is
−x+(Q−x)=−2×2000ε0=−4000ε0(C)
Hence, the equivalent capacity is
Ceq=Qε=4000ε020
or Ceq=200ε0(F).
Topper's Solved these Questions
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Solved Examples
10 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Exercise 4.1
13 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
Similar Questions
Each of the plates shown in figure ( 31- E19 ) has serface area (96ε0)×10−12Fm on one side and the seperation between the consecutive plates is 4.0 mm. The emf of the bettery connected is 10 volts . Find the magnitude of the charge supplied by the bettery to each of the plates connected to it .

View SolutionFind out equivalent capacitance between A and B. (take each plate Area = A)

View SolutionIn the following figures, area of each plate is A and d is separation between adjacent plates. Find the capacitance of system between points A and B.

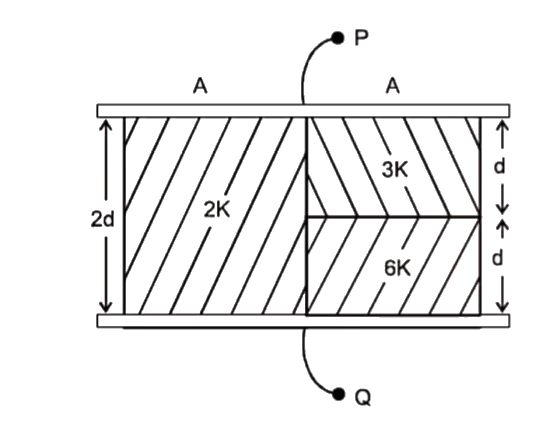
View SolutionThree different types of dielectric slabs have been arranged between the plates of a parallel plate capacitor, as shown in the figure. The equivalent capacitance of the system between the points P and Q will be
View SolutionSeven identical plates each of area A and successive separation d are arranged as shown in figures, the effective capacitance of the system between

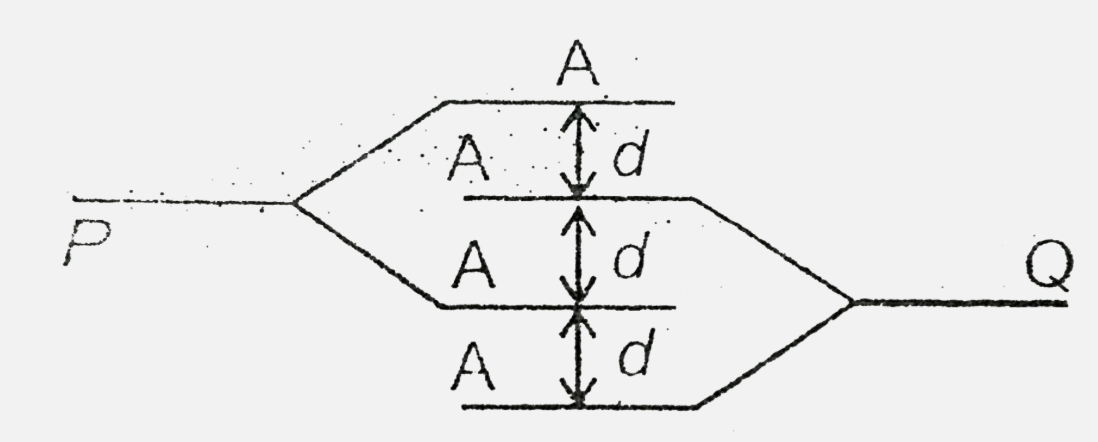
View SolutionIf the area of each plate is A and the separation between them is d, then find the equivalent capacitance between P and Q
View SolutionAll the plates shown in the figure are parallel to each other, the area of each plate is A, and the separation between each pair of facing plates is d. The equivalent capacitance between points A and B is
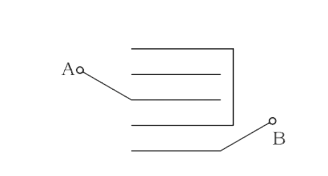
View SolutionFour metallic plates each with a surface area A of one side and placed at a distance d from each other. the plates are connected as shown in the fig. Then the capacitance of the system between a and b is -
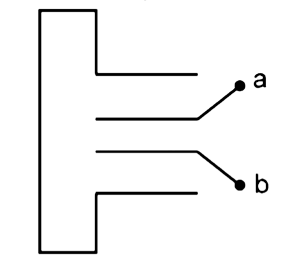
View SolutionIdentical metal plates are located in air at equal distance d from one another. The area of each plate is equl to A Evaluate the capacitance of the system between P and Q if the plates are interconnected as shown in.
 .
.
View SolutionSuppose n conducting face to face, and the distance between two successive plates is d. Each plate is half of the area of the previous one. If area of first plate is A
 .
.
(i) If the area of the first plate is A, find the equyivalent capacitance of the system.
(ii) If a cell of emf V is connected as shown in and a dielectric of dielectric constant k is inserted between the first and second plates, dind the charge on the nth plate.
View Solution
