Prove that if an isolated (isolated means no charges are near the sheet) large conducting sheet is given a charge, then the charge distributes equally on its two surfaces.
To prove that an isolated large conducting sheet distributes a given charge equally on its two surfaces, we can follow these steps:
1. Understanding the System:
- We have a large conducting sheet that is isolated, meaning there are no external electric fields or charges influencing it.
- When a charge Q is given to this conducting sheet, we need to show that this charge distributes equally on both surfaces of the sheet.
2. Defining Surface Charge Densities:
- Let the charge on one surface of the sheet be x.
- Consequently, the charge on the opposite surface will be Q−x since the total charge is Q.
3. Electric Field Due to a Single Sheet:
- The electric field E due to an infinite conducting sheet with surface charge density σ is given by:
E=σ2ϵ0
- Here, σ is the surface charge density, and ϵ0 is the permittivity of free space.
4. Calculating Electric Fields:
- For the surface with charge x, the electric field E1 at a point just outside the sheet is:
E1=x2ϵ0
- For the surface with charge Q−x, the electric field E2 at a point just outside this surface is:
E2=Q−x2ϵ0
5. Condition of Equilibrium:
- Since the conducting sheet is in electrostatic equilibrium, the electric fields due to both surfaces must be equal in magnitude but opposite in direction. Therefore, we can set:
E1=E2
- This gives us the equation:
x2ϵ0=Q−x2ϵ0
6. Solving the Equation:
- Canceling out 12ϵ0 from both sides, we have:
x=Q−x
- Rearranging this, we find:
2x=Q
- Thus, solving for x:
x=Q2
7. Conclusion:
- The charge on one surface is Q2 and the charge on the other surface is:
Q−x=Q−Q2=Q2
- Therefore, the charge distributes equally on both surfaces of the conducting sheet.
- We have a large conducting sheet that is isolated, meaning there are no external electric fields or charges influencing it.
- When a charge Q is given to this conducting sheet, we need to show that this charge distributes equally on both surfaces of the sheet.
- Let the charge on one surface of the sheet be x.
- Consequently, the charge on the opposite surface will be Q−x since the total charge is Q.
- The electric field E due to an infinite conducting sheet with surface charge density σ is given by:
E=σ2ϵ0
- Here, σ is the surface charge density, and ϵ0 is the permittivity of free space.
- For the surface with charge x, the electric field E1 at a point just outside the sheet is:
E1=x2ϵ0
- For the surface with charge Q−x, the electric field E2 at a point just outside this surface is:
E2=Q−x2ϵ0
- Since the conducting sheet is in electrostatic equilibrium, the electric fields due to both surfaces must be equal in magnitude but opposite in direction. Therefore, we can set:
E1=E2
- This gives us the equation:
x2ϵ0=Q−x2ϵ0
- Canceling out 12ϵ0 from both sides, we have:
x=Q−x
- Rearranging this, we find:
2x=Q
- Thus, solving for x:
x=Q2
- The charge on one surface is Q2 and the charge on the other surface is:
Q−x=Q−Q2=Q2
- Therefore, the charge distributes equally on both surfaces of the conducting sheet.
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Example
7 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.1
16 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
Similar Questions
A rubber balloon is given a charge Q distributed uniformly over its surface. Then
View SolutionThe net charge given to an isolated conducting solid sphere :
View SolutionA capacitor of capacitance 5μF is charged to potential 20V and isolated. Now, an uncharged capacitor is connected in parallel to it. If the charge distributes equally on these capacitors, find total energy stored in capacitors.
View SolutionTwo isolated metallic spheres of radii 2 cm and 4 cm are given equal charge, then the ratio of charge density on the surfaces of the spheres will be
View SolutionA point positive charge is brought near an isolated conducting sphere as shown in figure the electric field is best given by
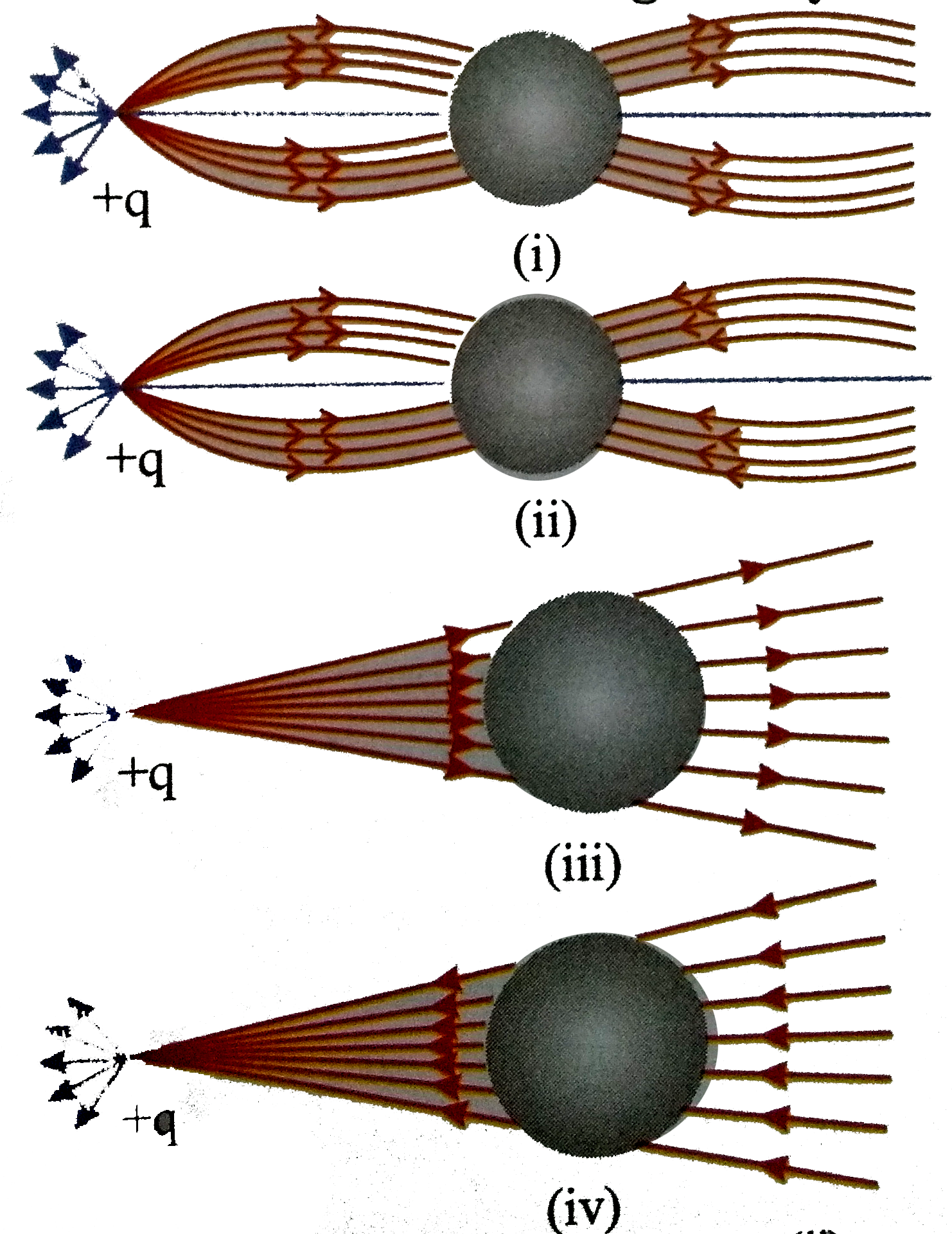
View SolutionA point positive charge is brought near an isolated conducting sphere. The electric field is best given by

View SolutionA point positive charge is brought near an isolated conducting sphere as shown in figure the electric field is best given by

View SolutionTwo conducting plates A and B are placed parallel to each other. A is given a charge. Q1 and B a charge Q2. Find the distribution of charges on the four surface.
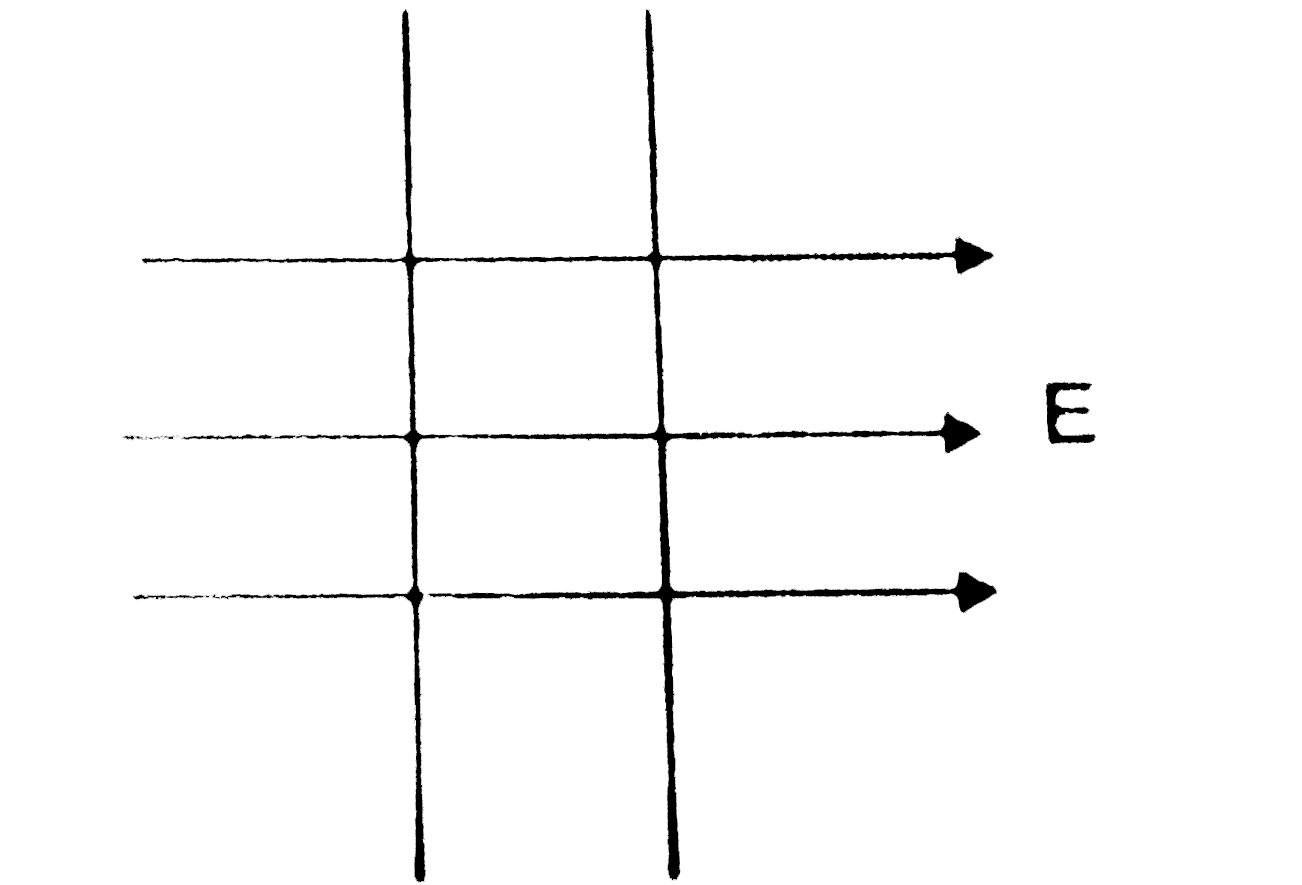
View SolutionTwo uncharged and parallel conducting sheets, each of area A are placed in a uniform electric field E at finite distance from each other, such that electric field is perpendicular to sheets and convers all the sheets. Find out charges appearing on its two surfaces.
View SolutionAn isolated conducting sheet of area A and carrying a charge Q is placed in a uniform electric field E, such that the electric field is perpendicular to the sheet and covers all the sheet. Find out the charges appearing on its two surfaces.

View Solution
