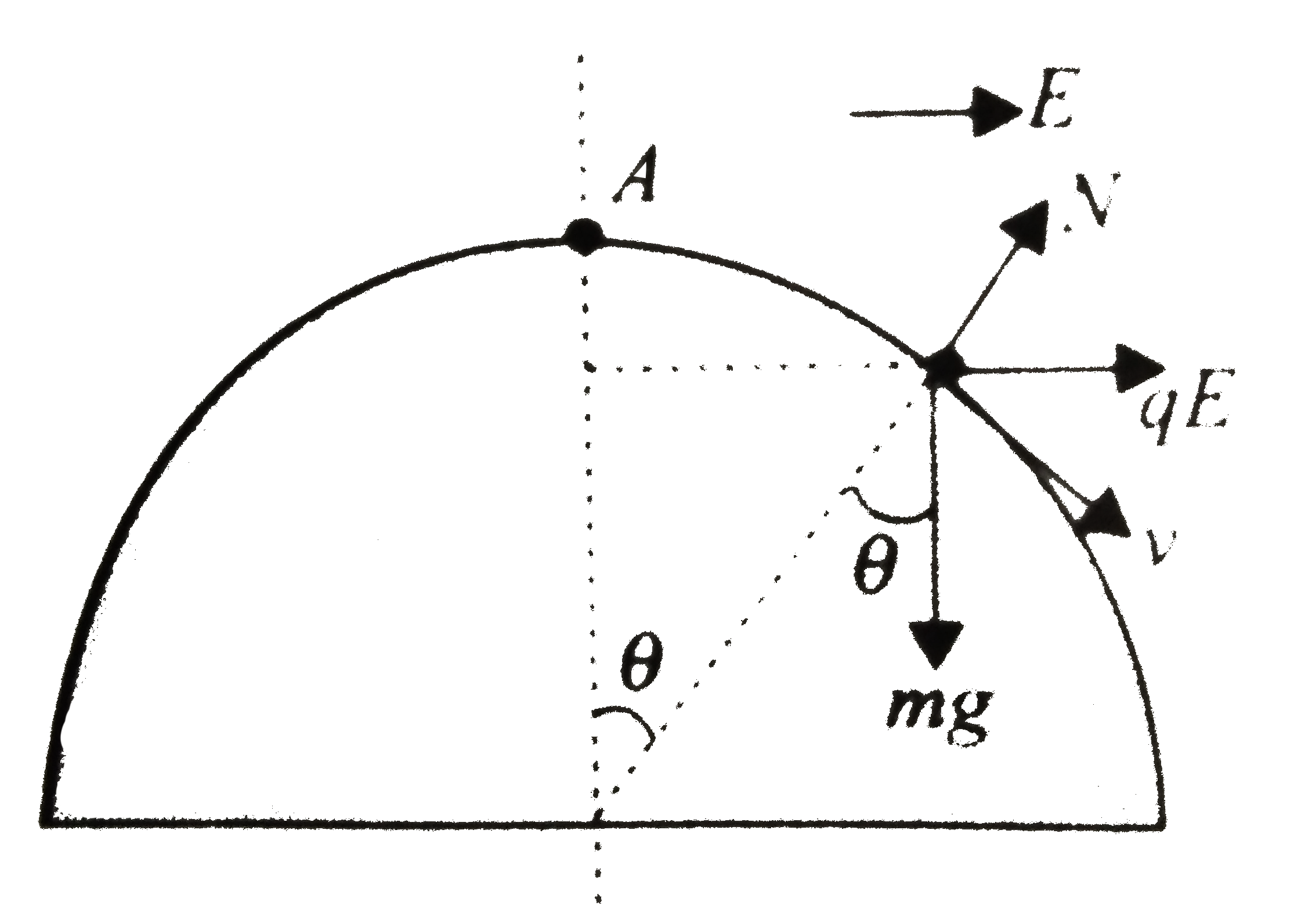
In a horizontal unifrom electirc field, a small charged disk is gently released on the top of a fixed sperical dome. The disk slides down the some without friction and breaks away from the surface of the dome at the angular position θ=sin−1(3/5) from vertical. Determine the ratio of the force of gravity acting on the disk to force of its interaction with the field .

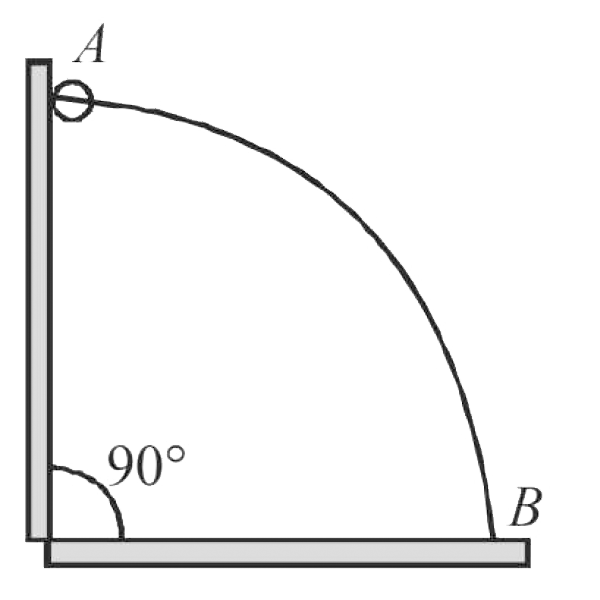
Motoin fron A to B
mgR(1−cosθ)+qERsinθ=mv22
Given sinθ=35
∴cosθ=45
∴mgR(15)+qER(35)=mv22
or (mg+3qE)=52mv2R …(i)
Also the equation of circular motion is
mgcosθ−N−qEsinθ=mv2R
When the paricle loses contact , N=0,sinθ=35, and cosθ=45.Therefore ,
mg(45)−qE(35)=mv2R
or, 4mg−3qE=5mv2R ...(ii)
Form Eqs, (i) and (ii), mg+3qE4mg−3qE=12
or, 2mg+6qE=4mg−3qE
or , 2mg=9qE or mgqE=92.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Exercises
58 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective Type
15 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type
22 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
A wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
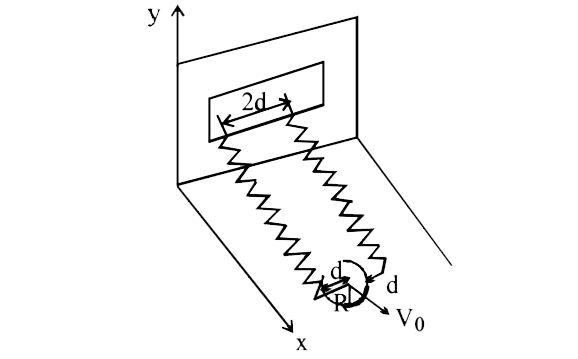
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.
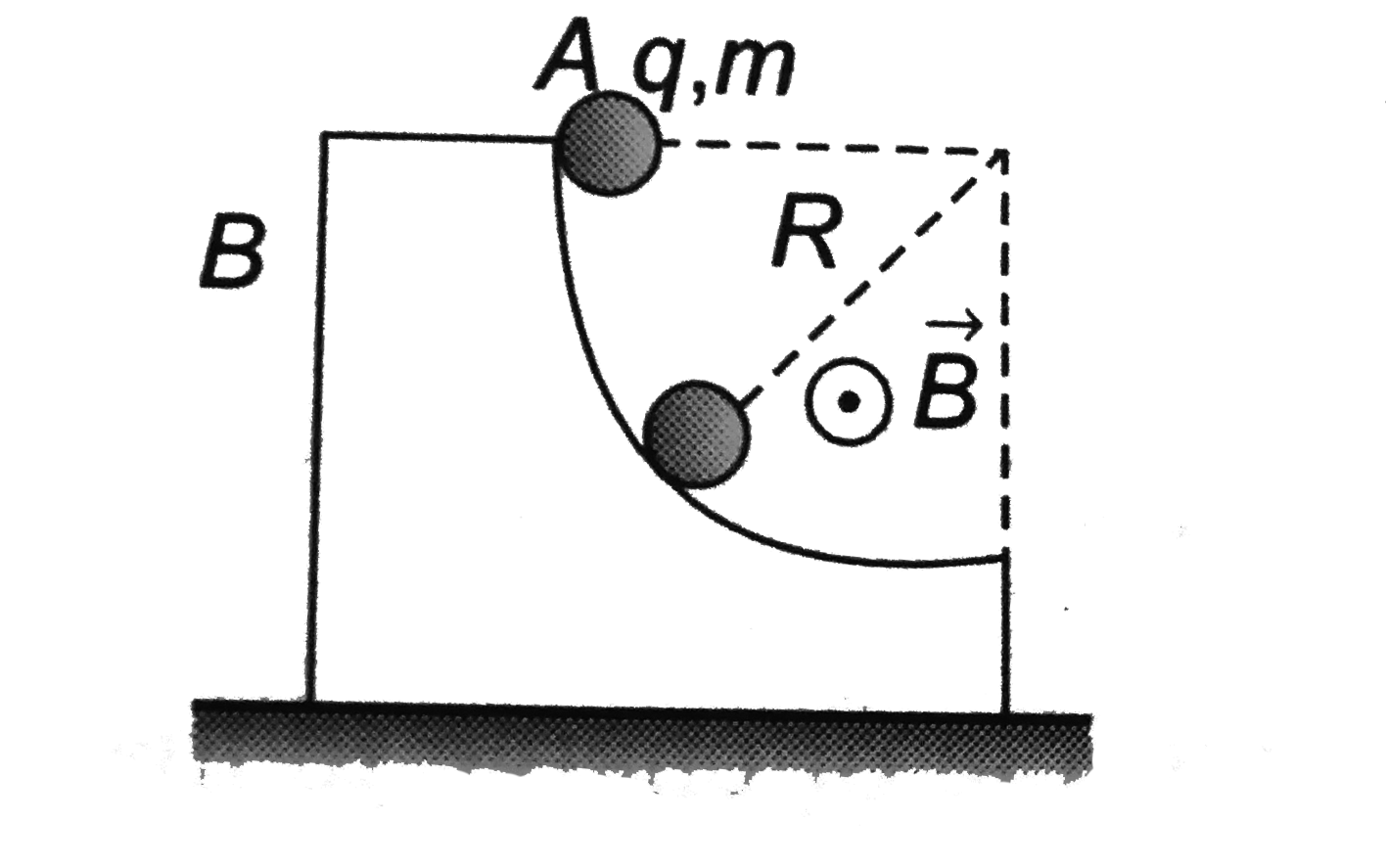
View SolutionIn the figure a charged small sphere of mass m and the charge q starts sliding from rest on a vertical fixed circular smooth track of radius R from the position A shown. There exist a uniform magnetic field of B. Find the maximum force exerted by track on the sphere during its motion.
View SolutionA uniform rod of maass m and length L is placed on the fixed cylindrical surface of radius R at an small angular position θ from the vertical (vertical means line joining centre and vertex of the cylindrical path) as shown in the figure and released from rest. Find the angular velocity ω of the rod at the instant when it crosses the horizontal position (Assume that when rod comes at horizontal position its mid point and vertex of the circular surface coincide). Friction is sufficient to prevent any slipping.

View SolutionA small circular coil with a mass of m consists of N turns of fine wire and carries a current of I. The coil is located in a uniform magnetic field of B with the coil axis orginally parallel to the field direction.

a. What is the period of small angle oscilations of the coil axis around its equilibrium position, assuming no friction and no mechanical force?
b. If the coil is rotated through an angle of θ from its equilibrium position and then released, what will be its angular speed when it passes through equilibrium position?
View SolutionA semicircular wire of radius R is oriented vertically. A small bead is released from rest from the top of the wire. It slides without friction under the influence of gravity to the bottom, where it then leaves the wire horizontally and falls distance H to the ground. The bead lands a horizontal distance D away from where it was launched. Which of the following is correct graph of RH vetsus D2?
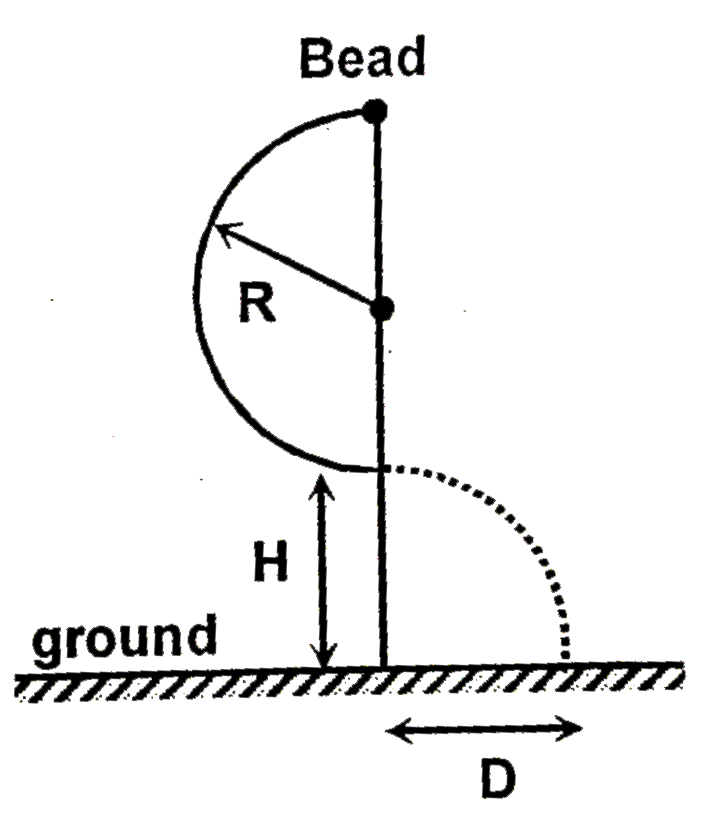
View SolutionOn end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37∘ with the horizontal. as shown in figure. When the system is released from rest, find the speed of the ring when the spring becomes horizontal. (sin37∘=35).

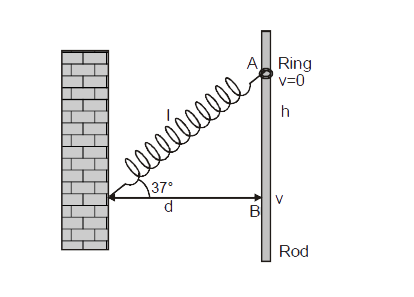
View SolutionOne end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37∘ with the horizontal as shown in fig. When the system is released from rest, find the speed of the ring when the spring becomes horizontal.
[ sin 37∘ = 3/5]
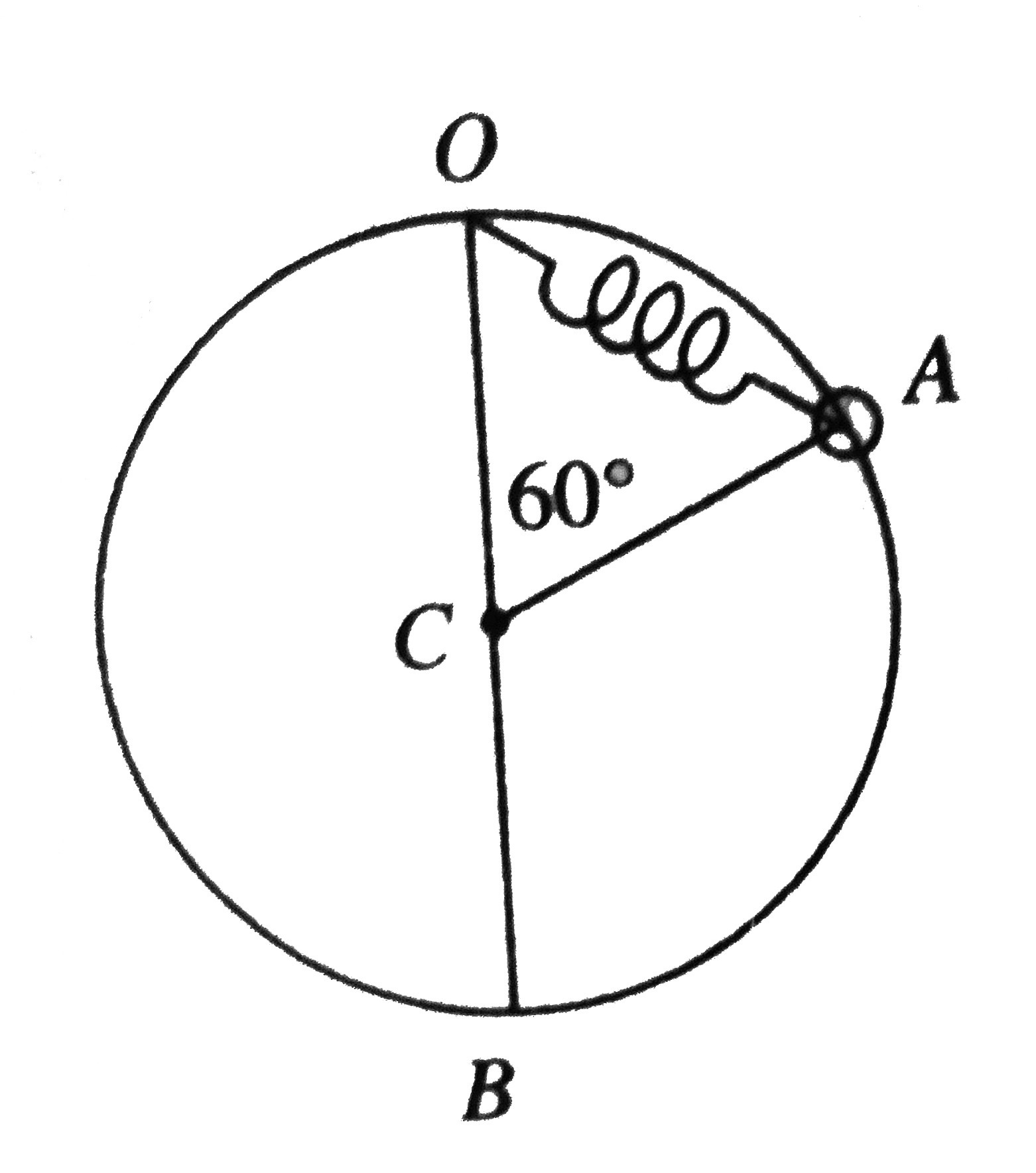
View SolutionA particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
View SolutionWhen liquid medicine of density ρ is to be put in the eye, it is done with the help of a dropper. As the bylb on the top of the dropper is pressed. A drop frons at the opening of the dropper. We wish to estimate the size of the drop.
We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy, To determine the size. We calculate the net vertical force due to the surface tension T when the radius of the drop is R. when this force become smaller than the weight of the drop the drop gets detached from the dropper.
If r=5×10−4m,ρ=103kgm−3,g=10ms−2,T=0.11Nm−1, The radius of the drop when it detaches from the dropper is approximately,
View Solution
